Suggerimenti per la costruzione
Lo strumento che è stato descritto alla pagina precedente, che rappresenta una variazione del cerchio di Ipparco è relativamente facile da calcolare ma credo che la sua costruzione sia impegnativa. Le difficoltà che immagino stanno nella scelta dei materiali adatti per costruire degli anelli sottili ma poco deformabili e nella costruzione di una struttura di sostegno che li tenga assieme e bene allineati.
1) Struttura complessiva
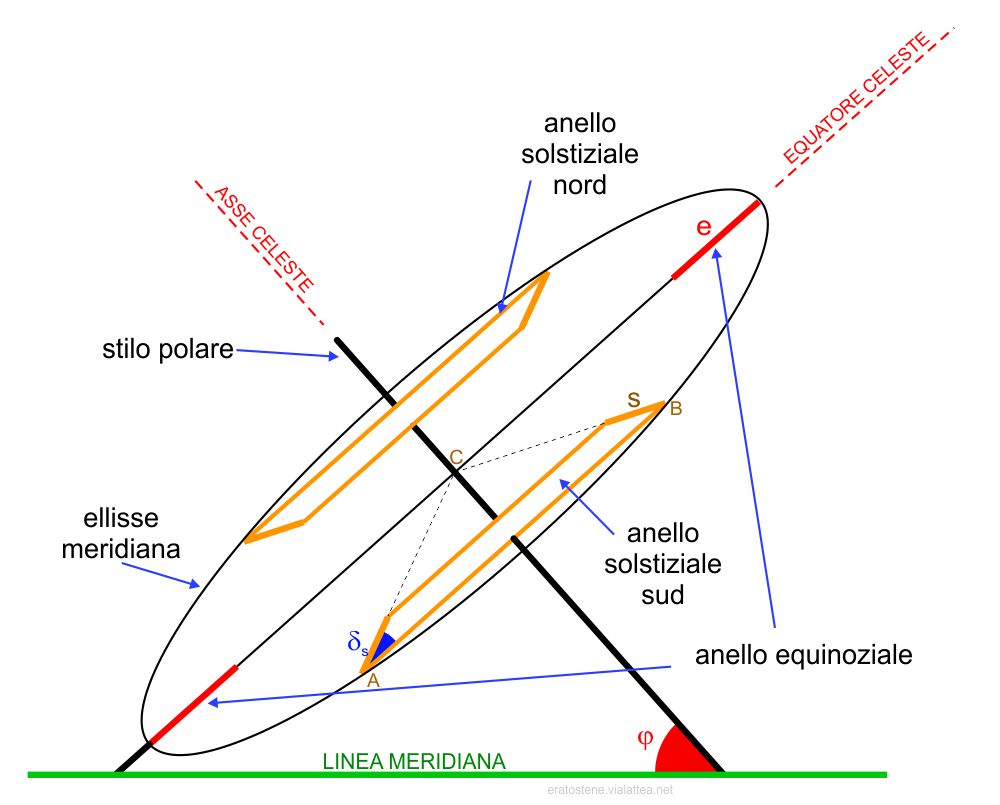
Lo schema a fianco rappresenta una sezione meridiana. Dell’anello equinoziale si vede la sua larghezza $e$. Gli anelli solstiziali sono rappresentati di profilo. In particolare, l’anello solstiziale sud è mostrato dentro al suo cono di costruzione $ABC$ con base $AB$ e vertice nel centro $C$ dello strumento. L’angolo $\delta_s$ è uguale a $\text{23,4}^\circ$.
Lo stilo polare è orientato, come dice il nome stesso, in direzione dell’asse celeste. Per fare questo, la sua inclinazione rispetto alla linea meridiana dev’essere un angolo pari alla latitudine del luogo $\varphi$.
L’intera struttura dei tre anelli e dello stilo polare è tenuta assieme da un’ellisse che dev’essere orientata con il piano meridiano. Per questo motivo la chiamo ellisse meridiana.
2) L’anello equinoziale
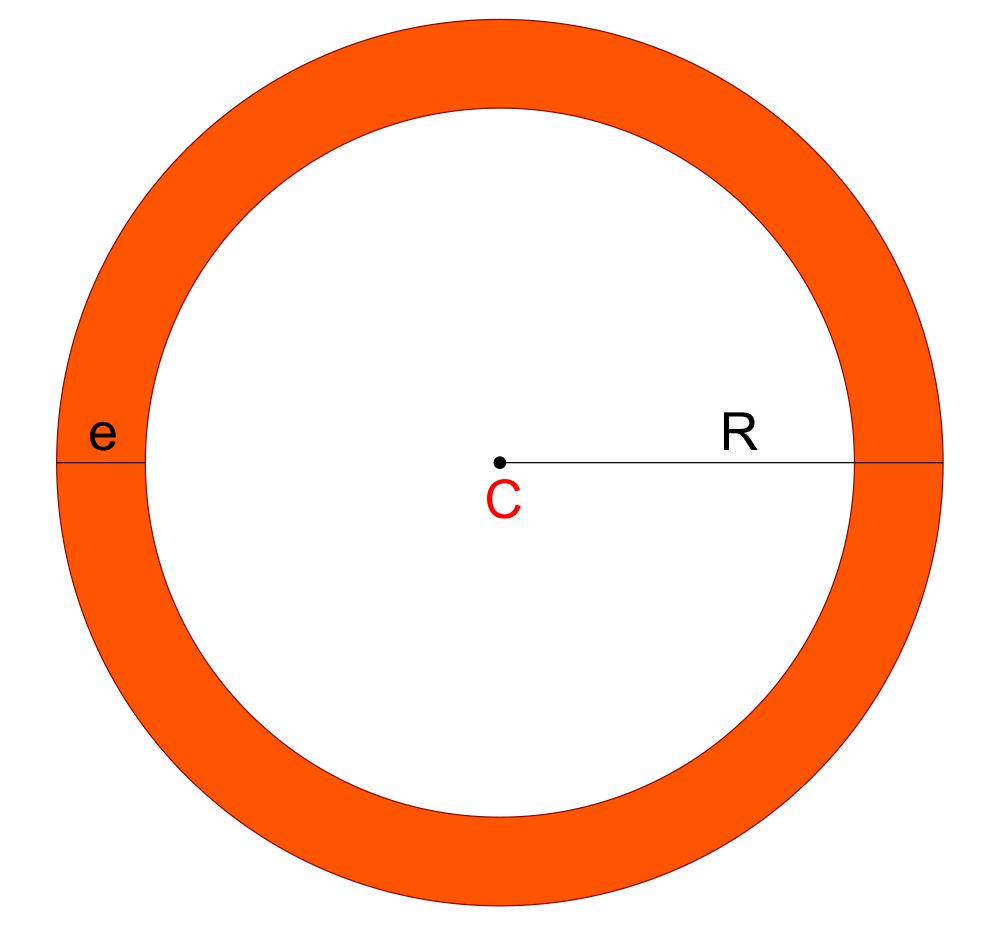
E’ un anello piatto. La scelta della misura del suo raggio esterno $R$ decide le dimesioni generali dello strumento. La larghezza $e$ dell’anello può essere scelta arbitrariamente. Dal rapporto tra $e$ e $R$ dipende anche lo spessore degli anelli solstiziali e delle ombre che proiettano. Io suggerirei all’incirca $e\simeq\frac{1}{5}R$.
3) Gli anelli solstiziali
Come si è detto gli anelli solstiziali sono superfici di tronchi di cono o fasce di una superficie conica la cui semiapertura dev’essere uguale a $90^\circ-\text{23,4}^\circ=\text{66,6}^\circ$. Per semapertura intendo l’angolo che la generatrice della superficie conica forma con il suo asse.
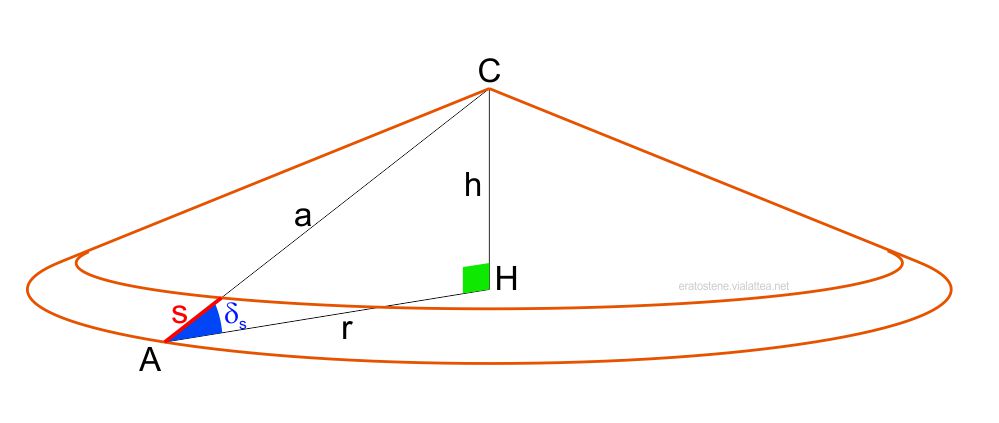
Nell’immagine qui a fianco si rappresenta il cono di costruzione dal quale si dovrà ritagliare la fascia per costruire l’anello solstiziale.
L’apotema del cono $a=CA$, la sua altezza $h=CH$ e il suo raggio $r=AH$ formano un triangolo rettangolo retto in $H$. La semiapertura è l’angolo $A\hat{C}H$. Di conseguenza l’angolo $C\hat{A}H=\delta_s$ dev’essere uguale, in valore assoluto, alla declinazione del Sole ai solstizi:
$$\delta_s = C\hat{A}H = \text{23,4}^\circ$$
Il raggio $r$ è il raggio esterno dell’anello solstiziale e dev’essere uguale alla metà del raggio $R$ dell’anello equinoziale. Le ragioni di ciò saranno spiegate in seguito. La larghezza $s$ della fascia conica non deve essere scelta a piacere ma dipende, come vedremo, dalla larghezza $e$ dell’anello equinoziale.
Di conseguenza, le misure di $a$, $r$ e $h$ si calcolano in funzione di $R$ con le seguenti formule:
$$r=\frac{R}{5}$$
$$h=r\tan{\delta_s}$$
$$a=\frac{r}{\cos{\delta_s}}$$
4) Come si producono le ombre?
Per ottenere l’estetica delle ombre descritte nella pagina introduttiva, sono necessarie alcune condizioni che esaminiamo con l’aiuto di una figura.
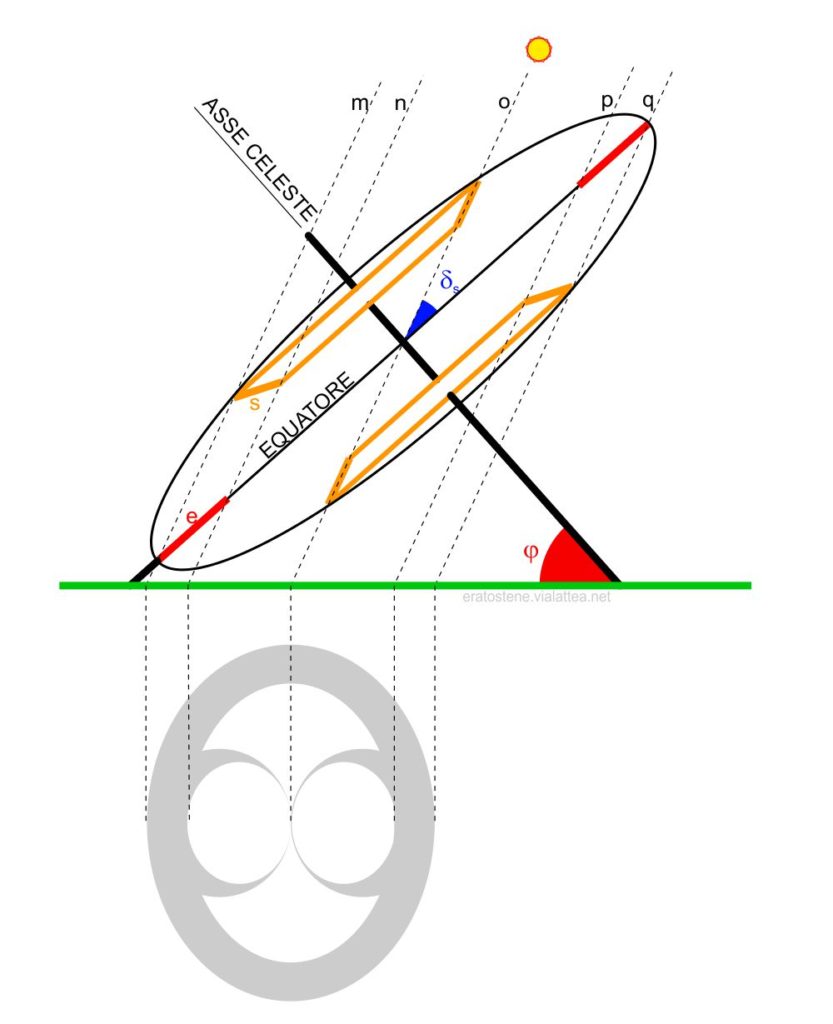
Lo strumento è posizionato con lo stilo polare in direzione dell’asse celeste e il disco equinoziale disposto sul piano dell’equatore celeste.
Si consideri il mezzogiorno vero di un solstizio di giugno. I raggi di sole ($m,n,o,p$ e $q$) scendono paralleli tra loro, con una certa inclinazioe rispetto al piano dell’orizzonte. Essi formano comunque un angolo $\delta_s$ con il piano dell’equatore. Gli anelli devono essere costruiti con le proporzioni e le distanze corrette in modo che:
- il raggio $m$ deve passare per i bordi esterni inferiori dell’anello solstiziale nord e dell’anello equinoziale, così come il raggio $q$ deve passare per i bordi esterni superiori dell’anello equinoziale e dell’anello solstiziale sud.
- il raggio $o$ che passa per il centro dello strumento deve passare “di taglio” per il bordo superiore dell’anello solstiziale nord e per quello inferiore dell’anello solstiziale sud. In questo modo esso proietterà l’ombra del punto centrale di tangenza delle ombre degli anelli solstiziali.
- I raggi $n$ e $p$, passando per i bordi interni degli anelli, dimostrano che, se si desidera ottenere un’ombra complessiva esteticamente valida, le larghezze $e$ e $s$ degli anelli non possono essere scelte a caso ma devono essere in relazione matematica tra loro.
5) Proporzioni complessive
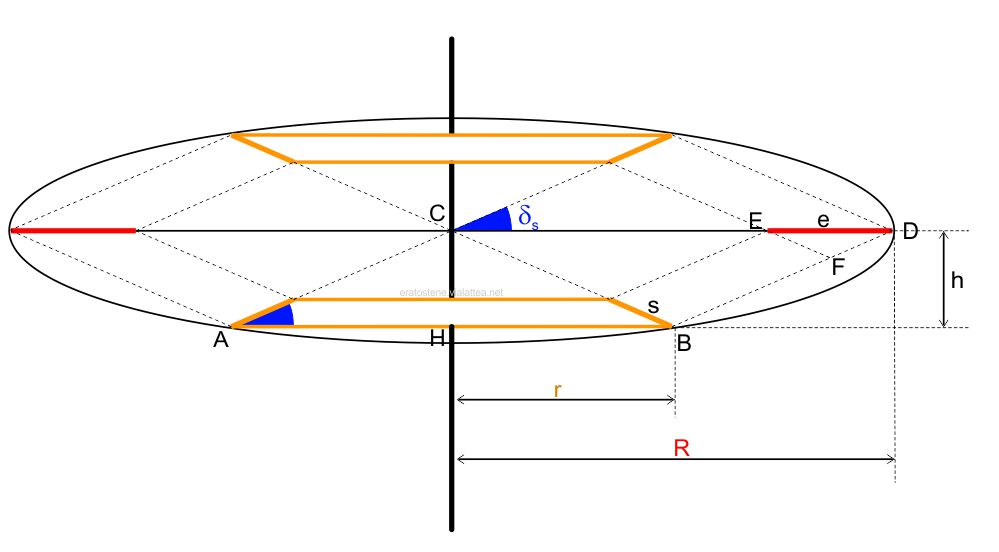
Il rispetto delle regole per la costruzione di un’ombra esteticamente valida impone delle proporzioni e delle distanze precise. Le proporzioni che ne risultano sono inaspettatamente facili da calcolare. Se si osserva la figura, si scopre che tutti i triangoli disegnati sono isosceli e congruenti o simili tra loro. Ciò è dovuto alla ripetizione dell’angolo $\delta_s$ in ognuno di essi. In particolare, il triangolo $CAB$, che è la sezione del cono descritto prima, è congruente al triangolo il triangolo $CBD$. Ne deriva che la base $AB=2r=R$, perciò ecco il motivo per cui il raggio $r$ degli anelli solstiziali deve essere la metà del raggio $R$ degli anelli equinoziali.
Inoltre, la similitudine tra il triangolo $CBD$ e il triangolo $EFD$ ci permette di calcolare con una semplice proporzione la larghezza $s$ degli anelli solstiziali in funzione della larghezza $e$ dell’anello equinoziale che, come abbiamo detto, può essere scelto a piacere:
$$\frac{EF}{ED}=\frac{CB}{CD}$$
Sapendo che $CB$ è l’apotema $a$ del cono descritto prima, $CD$ è il raggio $R$ dell’anello equinoziale, $ED$ è la sua larghezza $e$, ed infine $EF$ è uguale alla larghezza $s$ dell’anello solstiziale, possiamo scrivere più semplicemente:
$$\frac{s}{e}=\frac{a}{R}$$
e quindi calcolare $s$ in funzione degli altri parametri:
$$s=\frac{ae}{R}$$
6) Come costruire la fascia degli anelli solstiziali?
Se si riprende a osservare la seconda figura di questa pagina, la fascia descritta di larghezza $s$ è una parte della superficie conica di un cono di cui sono noti l’apotema $a$, e il raggio $r$. Se si sviluppa la superficie conica ritagliandola lungo un suo apotema e la si appiattisce, si ottiene un settore circolare.
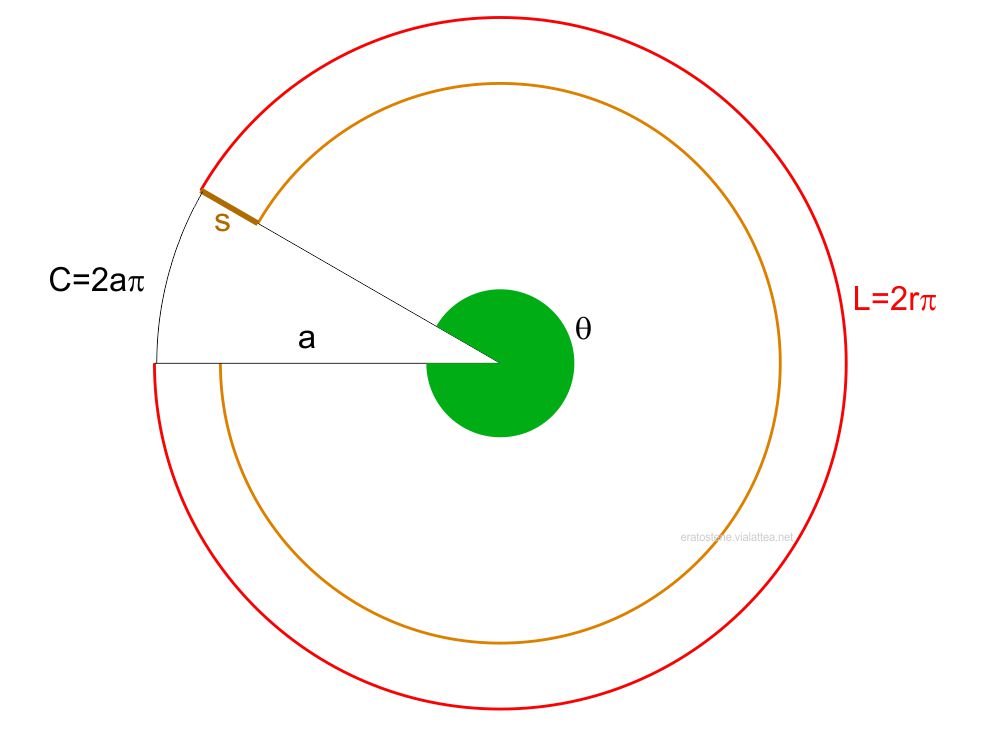
Il settore sottende un arco lungo $L=2r\pi$ perché è uguale alla circonferenza di base del cono decritto al paragrafo 3; questo settore fa parte di una circonferenza $C$ il cui raggio è uguale all’apotema $a$ del cono, perciò essa è lunga:
$$C=2a\pi$$
Per calcolare l’ampiezza $\theta$ di questo settore, che è il dato utile per la costruzione della fascetta, si può far ricorso alla proporzionalità che esiste tra gli archi e gli angoli al centro corrispondenti:
$$\frac{L}{C}=\frac{\theta}{360^\circ}$$
da cui:
$$\theta = \frac{L\cdot360^\circ}{C}=\frac{2r\pi\cdot360^\circ}{2a\pi}=\frac{r}{a}\cdot360^\circ$$
Il rapporto $\frac{r}{a}$ è facilmente deducibile dal triangolo rettangolo $CHA$ descritto al paragrafo 3:
$$\frac{r}{a}=\cos{\delta_s}$$
per cui si calcola $\theta$ in questo modo:
$$\theta = 360^\circ\cdot\cos{\delta_s} =330^\circ$$
7) Posizionamento dello strumento
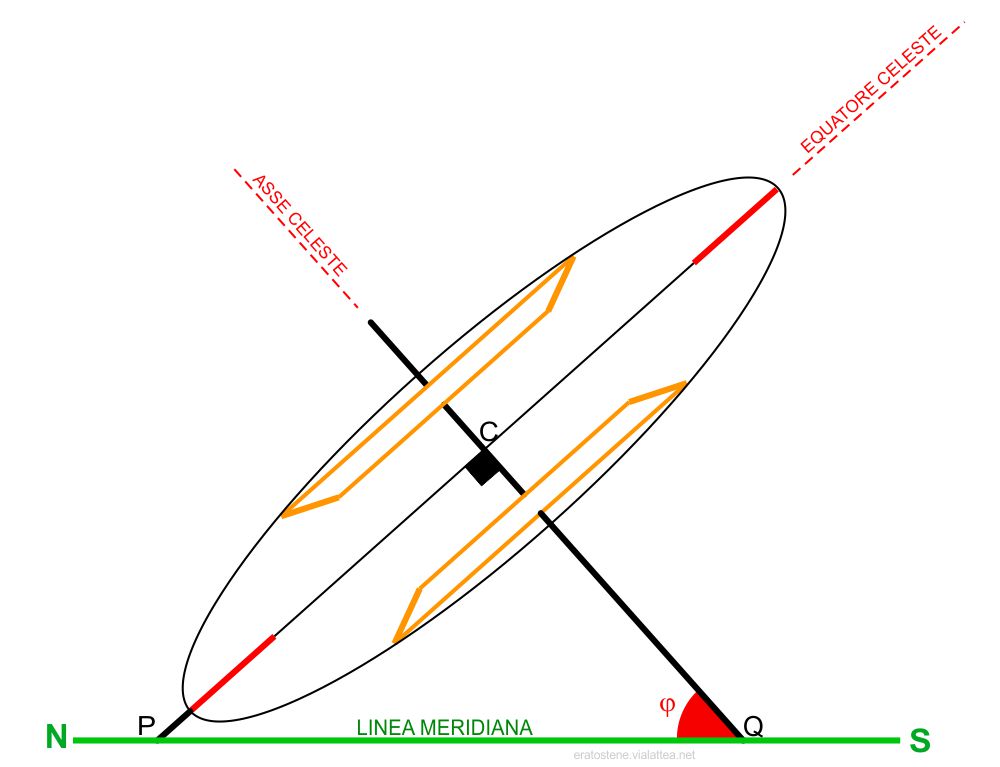
Il triangolo di sostegno $CPQ$ è retto in $C$. Conviene partire dalla scelta della distanza $CP$ che dev’essere maggiore di $R$ e quindi calcolare gli altri due lati:
$$PQ = \frac{CP}{\sin{\varphi}}$$
$$CQ=\frac{PC}{\tan{\varphi}}$$
8) Un esempio di calcolo
INPUT
$R=25$ Raggio dell’anello equinoziale
$e=6$ Larghezza dell’anello equinoziale
$CP=30$ Sostegno
$\varphi=42^\circ$ Latitudine
OUTPUT
$r=\text{12,4}$ Raggio degli anelli solstiziali
$h=\text{5,4}$ Distanza tra gli anelli solstiziali e l’anello equinoziale
$a=\text{13,6}$ Apotema del cono e raggio del cerchio per la costruzione della fascia solstiziale
$s=\text{3,3}$ larghezza della fascia solstiziale
$PQ=\text{44,8}$ Base di appoggio
$CQ=\text{33,3}$ Segmento di stilo di appoggio dal centro dello strumento

