La suddivisione dell’orbita circolare del Sole
L’equatorium, come pure la teoria che sta alla sua base, nasce dalle durate delle stagioni. Costruiamo un equatorium adatto alla nostra epoca prendendo come riferimento le durate delle stagioni dell’anno 2022 (1):
primavera: $92^d17^h40^m = 92,7364^d$
estate: $93^d15^h50^m = 93,6596^d$
autunno: $89^d20^h44^m = 89,8642^d$
inverno: $88^d23^h34^m =88,9820^d$
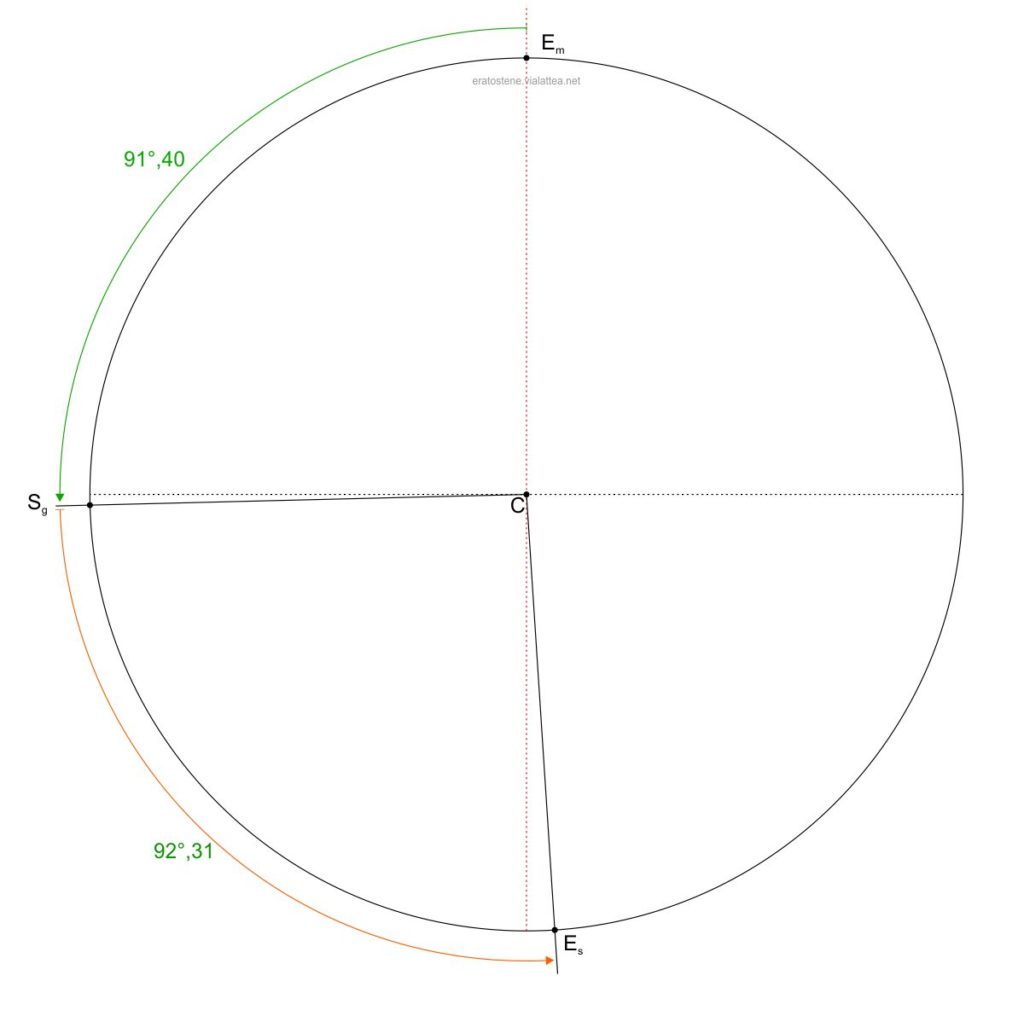
Disegniamo una circonferenza grande a piacere che rappresenta il circolo dell’orbita solare. Per un disegno accurato si consiglia un raggio di circa $20 cm$. La sua lunghezza corrisponde alla lunghezza dell’anno tropico, di $\text{365,25}$ giorni. Il suo centro è il punto $C$. Scegliamo un punto $E_m$ qualsiasi sulla circonferenza per indicare la posizione del Sole all’equinozio di marzo. Ci proponiamo di posizionare correttamente il punto $S_g$ del solstizio di giugno successivo. Se le quattro stagioni fossero di uguale durate, il loro arco sarebbe lungo $\text{365,25/4=91,31}$ giorni per ciascuna, corrispondenti ad un angolo di $90^\circ$. La lunghezza della primavera astronomica boreale è invece di $\text{92,7364}$ giorni e l’arco corrispondente è:
$$\frac{\text{92,7364}^d}{\text{365,25}^d}\cdot360^\circ=91^\circ,\!4034$$
Partendo da $E_m$ misuriamo perciò un angolo di $91^\circ,\!4$ e fissiamo il punto $S_g$
Analogamente, partendo dal punto $S_g$ apriamo con un arco corrispondente alla durata dell’estate che calcoliamo così:
$$\frac{\text{93,6596}^d}{\text{365,25}^d}\cdot360^\circ=92^\circ,\!3134$$
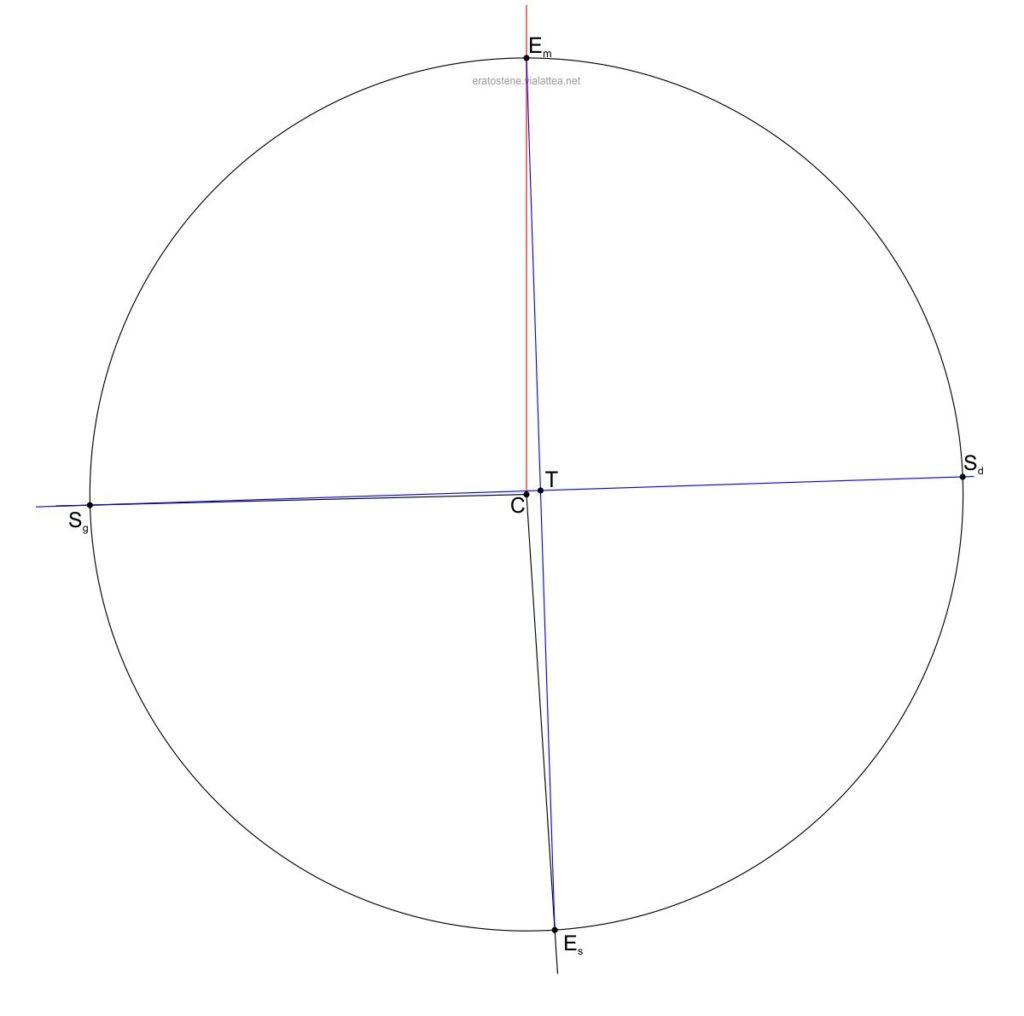
Potremmo completare con le altre due stagioni, ma essendo le loro posizioni reciproche lungo l’eclittica separate da angoli di $90^\circ$, possiamo continuare graficamente tracciando il segmento $E_sE_m$ (che non è un diametro!) ed infine tracciando la perpendicolare a quest’ultimo che passa per $S_g$. Questa seconda retta incontra la circonferenza nel punto $S_d$ del solstizio di dicembre e incontra la prima nel punto $T$ che è la posizione della Terra al centro della sfera celeste.
E’ bene prestare attenzione alla precisione del disegno e alle sue dimensioni. La distanza $CT$ è molto piccola. Come esempio, se il raggio del cerchio è $20 cm$ il segmento $CT$ è di soli $\text{6,7} mm$.
Abbiamo così ottenuto quattro archi tutti diversi tra loro, le cui lunghezze sono proporzionali alle durate delle stagioni.
(1) Le durate sono state calcolate utilizzando Skyfield e ho mantenuto un’esagerata precisione dell’ordine del minuto solo perché non è scomodo farlo. Le misurazioni dei solstizi e degli equinozi ai tempi di Ipparco e di Tolomeo non potevano avere una precisione maggiore dell’ordine del quarto di giorno. La scelta dell’anno ha scarsa importanza per i nostri scopi: sia la longitudine dell’afelio che l’eccentricità variano molto poco nel corso degli anni. La variazione diventa sensibile dopo vari decenni. Ho scelto un anno intermedio tra due bisestili solo perché rappresenta meglio i valori medi della longitudine del Sole se si vuol fare un confronto successivo.

