E’ uno strumento solare descritto da Tolomeo nell’Almagesto. E’ un semplice anello posizionato sul piano dell’equatore celeste. La sua principale funzione era quella di determinare gli istanti degli equinozi. Qualsiasi oggetto piano e sottile posizionato con la stessa giacitura del piano dell’equatore celeste, nei giorni degli equinozi proietterà un’ombra rettilinea, sottile quanto il suo spessore. Non solo: l’ombra rettilinea proiettata sarà parallela alla linea equinoziale. Se il piano di proiezione dell’ombra è orizzontale, tale linea coincide con la linea est-ovest.
In base a questa idea possiamo costruire uno strumento noto come cerchio di Ipparco, armilla equinoziale o anche anello equatoriale, che è teoricamente in grado di segnare l’istante di un equinozio semplicemente osservando come si proiettano le ombre. Si tratta sostanzialmente di un anello circolare che simula l’equatore celeste perché è posizionato sul suo stesso piano.
La costruzione di un cerchio di Ipparco richiede tre operazioni preliminari:
- su un piano orizzontale si traccia la linea meridiana (vedi metodo dei cerchi indù);
- sullo stesso piano si traccia anche la linea est-ovest, perpendicolare alla linea meridiana;
- è necessario conoscere la misura della latitudine astronomica del luogo in cui si installa lo strumento: la relativa colatitudine determina l’inclinazione dell’anello rispetto al piano orizzontale.
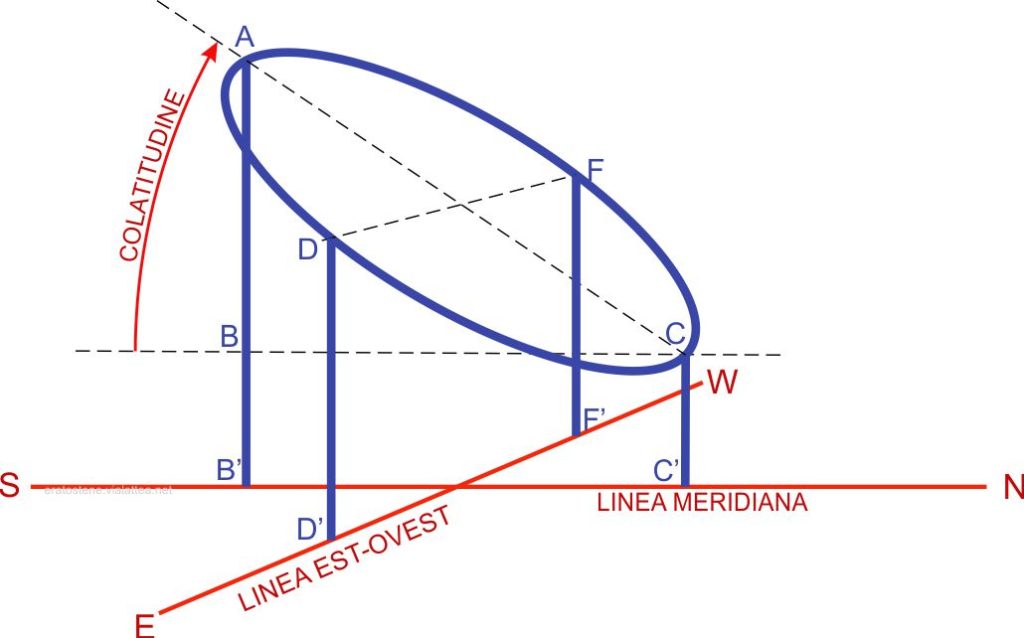
Come è stato detto, il cerchio di Ipparco è un modello orientato del circolo dell’equatore celeste. Perciò il diametro $AC$ dell’anello deve trovarsi nel piano meridiano. Due dei quattro sostegni verticali, $AB’$ e $CC’$, devono avere i piedi $B’$ e $C’$ sulla linea meridiana precedentemente tracciata. Il diametro orizzontale $DF$, perpendicolare al diametro $AC$, deve invece essere parallelo alla linea est-ovest. Perciò gli altri due sostegni verticali $DD’$ e $FF’$ devono avere i loro piedi $D’$ e $F’$ sulla linea est-ovest.
Partendo da due misure note, il diametro $d$ del cerchio e la colatitudine $\varphi’$ il triangolo $ABC$ si risolve facilmente per mezzo delle seguenti formule:
$$\overline{BC}=d\cos{\varphi’}$$
$$\overline{AB}=d\sin{\varphi’}$$
L’altezza dei sostegni è scelta a piacere e calcolata partendo dalla misura di $CC’$:
$$\overline{AB’}=\overline{AB}+\overline{CC’}$$
$$\overline{DD’}=\overline{FF’}=\frac{\overline{AB}}{2}+\overline{CC’}$$
Come leggere le ombre del cerchio di Ipparco
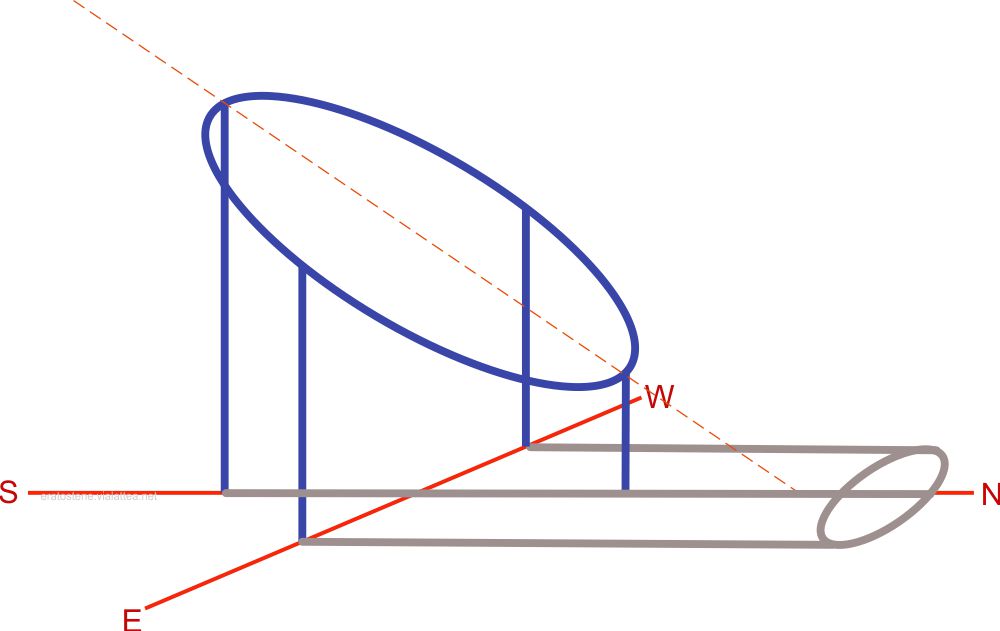
In un giorno compreso tra l’equinozio di settembre e l’equinozio di marzo, il Sole si trova nell’emisfero celeste sud, cioè al di sotto del piano dell’equatore celeste e la sua altezza non raggiunge mai la colatitudine. Perciò l’ombra del cerchio di Ipparco sul piano orizzontale è un’ellisse. Qui si rappresenta l’ombra all’istante del mezzogiorno, cioè del transito del Sole al meridiano. Infatti i due sostegni verticali posti sulla linea meridiana sovrappongono le loro ombre ad essa.
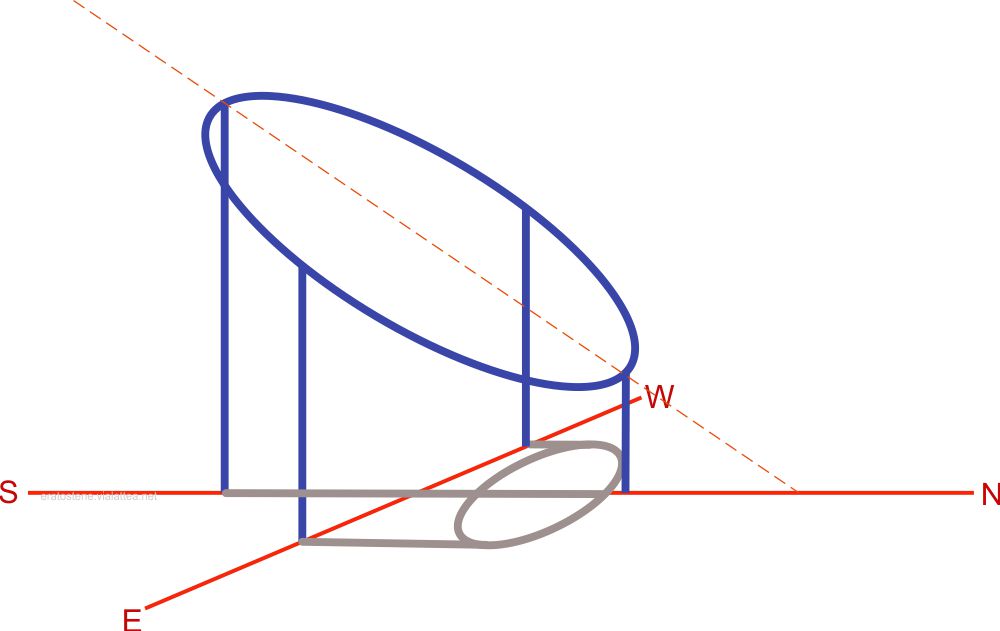
In un giorno compreso tra l’equinozio di giugno e quello di settembre il Sole si trova nell’emisfero nord, cioè al di sopra del piano del cerchio di Ipparco e la sua ombra proiettata sul piano è ancora un’ellisse. Anche qui l’ombra disegnata nell’immagine è quella del mezzogiorno solare.
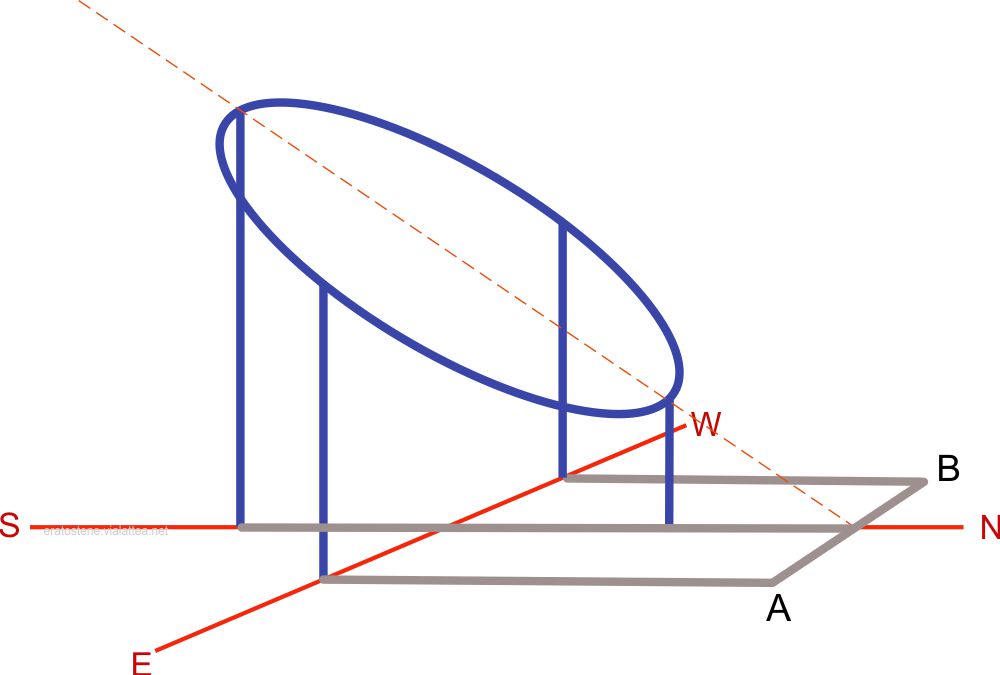
Nell’istante di un equinozio il Sole si trova sullo stesso piano del cerchio di Ipparco, cioè sul piano dell’equatore celeste. L’ombra del semicerchio posto a sud cade sul lato interno del semicerchio posto a nord e l’ombra risultante sul piano è un segmento ($AB$) parallelo alla linea est-ovest. Dato che il Sole non è una sorgente puntiforme, l’arco superiore proietta sull’arco inferiore un’ombra leggermente più sottile dello spessore dell’anello per cui l’equinozio può essere controllato con precisione osservando l’uguaglianza dei due bordi illuminati, laterali all’ombra.
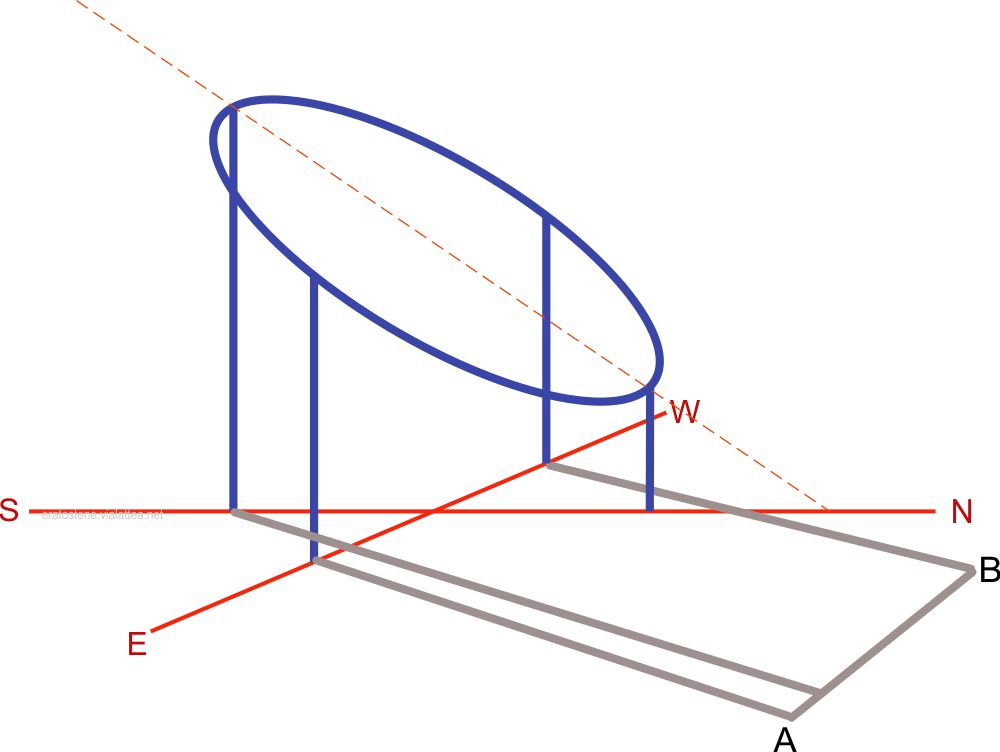
Nel giorno in cui cade un equinozio, in una qualsiasi ora di luce, l’ombra del cerchio di Ipparco tende a conservare la forma di un segmento parallelo alla linea est-ovest perché il Sole permane comunque in posizione molto prossima all’equatore. Nell’immagine a fianco si rappresenta l’ombra equinoziale di un’ora pomeridiana.
L’anello equatoriale è descritto da Tolomeo nell’Almagesto. Assieme al quadrante meridiano (noto come plinto di Tolomeo) è uno degli strumenti da lui usati per identificare gli istanti degli equinozi. Il pregio dell’anello equatoriale rispetto al quadrante meridiano è quello che permette di identificare il momento dell’equinozio se esso cade in una qualsiasi ora di luce, mentre il quadrante meridiano misura l’altezza del Sole soltanto nel momento del suo transito sul piano meridiano. D’altra parte il cerchio è uno strumento valido solo se è accuratamente orientato. Inoltre, il controllo dei bordi di penombra descritto prima è poco preciso per altezze del Sole inferiori a $15^\circ$. Infatti, quando il Sole è molto basso sull’orizzonte interviene l’effetto della rifrazione atmosferica che può indurre un errore sensibile aumentando l’altezza apparente anche di mezzo grado. Oltre i $15^\circ$ invece l’innalzamento dell’immagine del Sole è inferiore ai $3^\prime$. L’effetto della rifrazione, in condizioni particolari, può provocare anche un apparente doppio equinozio nel corso della stessa giornata.
La pagina successiva contiene il resoconto di un’esperienza scolastica sulla costruzione del cerchio di Ipparco.
Torna a:

