Una sfera armillare di cartoncino

L’armilla o sfera armillare è un antico strumento astronomico usato sia per misurare le coordinate degli astri, sia come modello didattico della sfera celeste con i suoi principali circoli. I circoli erano rappresentati per mezzo di anelli⁽¹⁾ dotati di scale graduate, alcuni dei quali in grado di ruotare rispetto ad altri. La più antica descrizione di questo strumento è contenuta nell’Almagesto di Tolomeo risalente al 150 d.C. Esso permetteva di misurare le coordinate eclittiche degli astri. Successivamente, gli astronomi islamici e rinascimentali costruirono grandi armillle di vario tipo, dotate di scale dettagliate e di alidade con traguardi, usate per misurare diverse coordinate degli astri. Si costruivano anche modelli più piccoli, utili per dimostrare i principi dell’astronomia sferica e dei moti dei corpi celesti. Questi ultimi erano arricchiti con ulteriori anelli che rappresentavano il Sole, la Luna e i pianeti. (nella foto: un’armilla di Girolamo della Volpaia, Firenze 1564, catalogo del Museo di Galileo)

Le parti del modello, da stampare in A4 e ritagliare, sono contenute in questo file PDF:

Quasi tutti gli anelli (a parte quello dell’orizzonte) hanno due facce che vanno ritagliate e incollate tra loro. La struttura compessiva diventa così più robusta pur utilizzando un cartoncino non troppo spesso.

Descriviamo qui di seguito le varie parti dell’armilla e il metodo di costruzione.

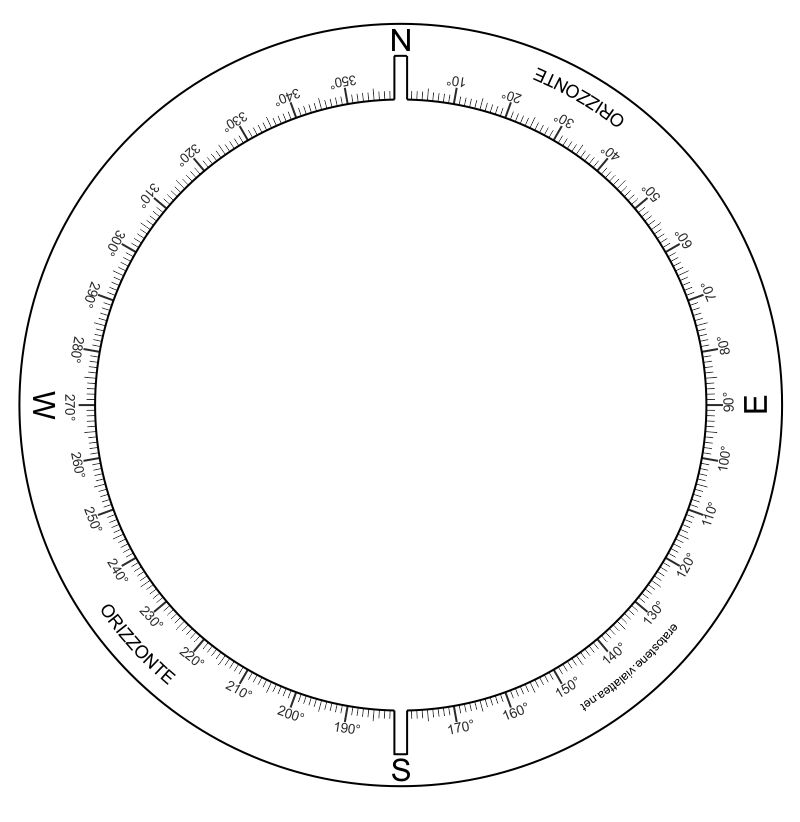
L’anello dell’orizzonte si appoggia alla base per mezzo di quattro sostegni costruibili utilizzando i modelli in cartoncino ritagliabili. Un soluzione migliore è costruirli in legno. L’altezza dei sostegni deve essere uguale al raggio esterno dell’anello meridiano così che quest’ultimo possa appoggiare sul piano.

L’anello dell’orizzonte ha due scanalature nelle quali si dovrà infilare l’anello meridiano in posizione verticale. La scala rappresentata è l’azimut che origina con $0^\circ$ nel punto cardinale nord $N$ e si conta in senso orario.

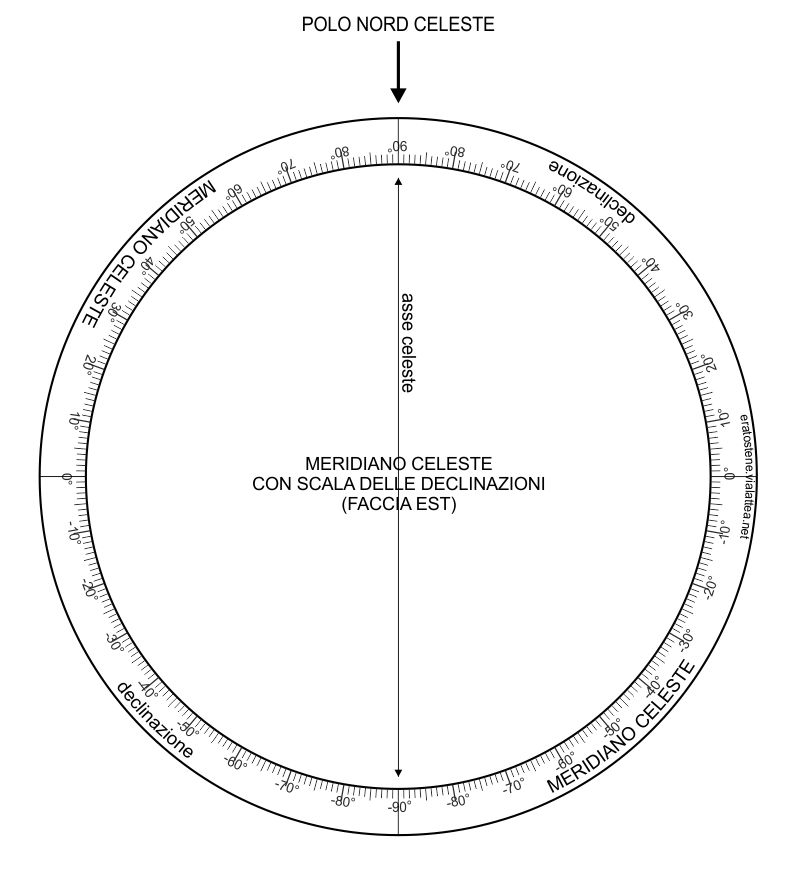
Il circolo del meridiano celeste è composto di due facce che dovranno essere incollate tra loro facendo coincidere tra loro i poli. La faccia rivolta all’emisfero est è dotata di una doppia scala delle decliazioni. La declinazione $0^\circ$ indica la posizione dell’equatore celeste che sarà disposto perpendicolarmente. Le declinazioni $+90^\circ$ e $-90°$, corrispondenti ai poli celesti nord e sud, sono anche i punto dove sarà incollato il bastoncino dell’asse celeste. Quest’ultima sosterrà la struttura “rigida” formata da tutti gli altri anelli (equatore, eclittica, tropici e coluri) e ne permetterà la rotazione rispetto al meridiano.

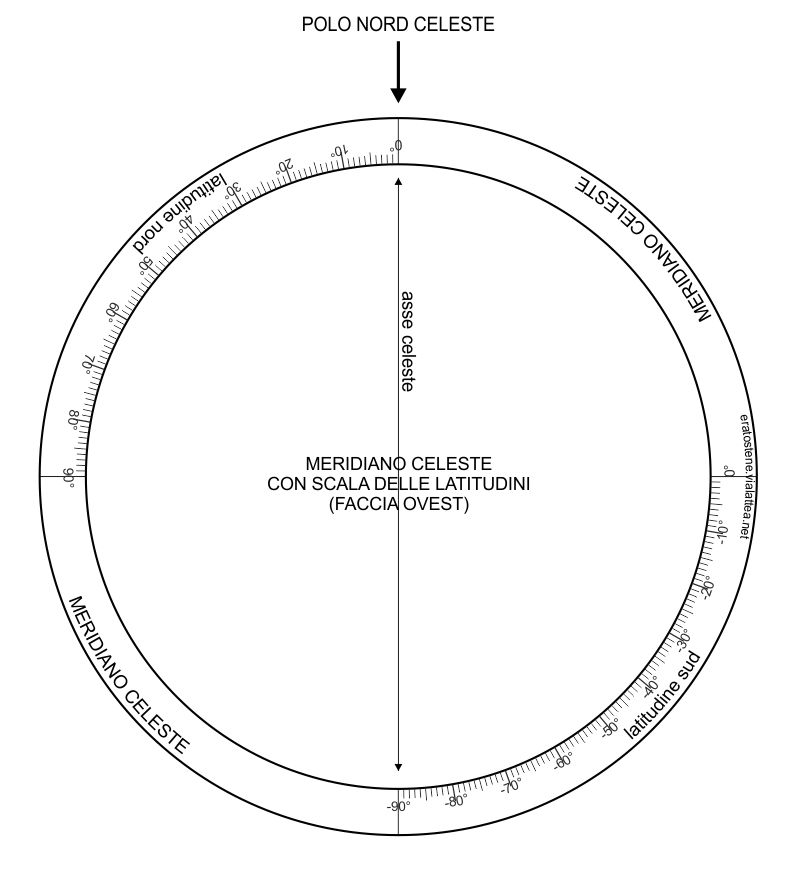
La faccia rivolta a ovest del meridiano celeste contiene due scale di latitudine: una quadrante di latitudine nord con valori positivi e un quadrante di latitudine sud con valori negativi. Queste due scale servono per posizionare il meridiano rispetto all’anello dell’orizzonte. La tacca corrispondente alla latitudine desiderata dovrà trovarsi sul piano dell’orizzonte.

L’anello meridiano dovrà essere fatto di un cartoncino piuttosto robusto, preferibilmente più spesso di quello che si userà per gli altri anelli. Esso ha tre punti di ancoraggio: le due scanalature dell’anello dell’orizzonte e il punto di appoggio nel punto centrale della base. Per mantenere l’assetto è conveniente applicare sulla base in corrispondenza del punto di appoggio due guide di cartoncino tra le quali infilare l’anello meridiano.

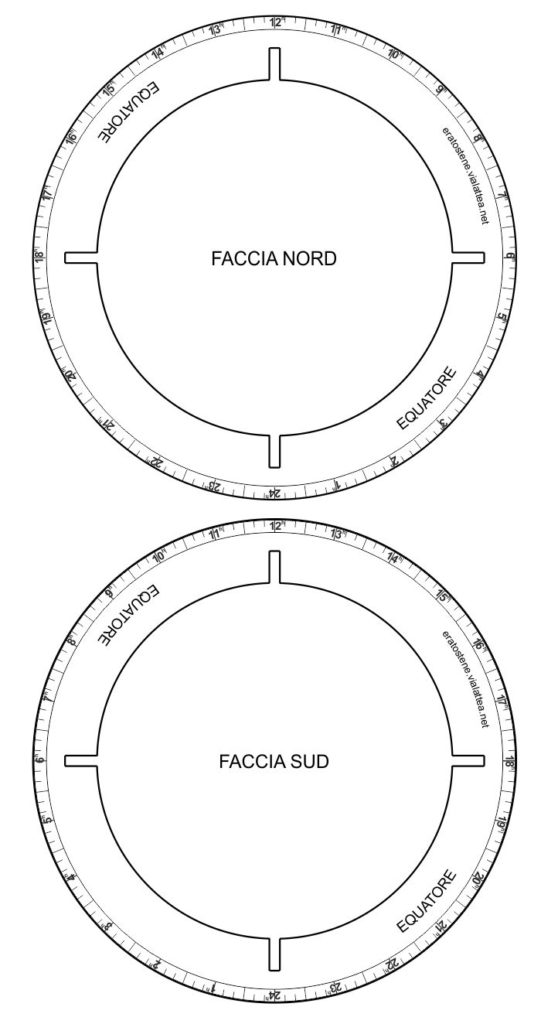
L’equatore si costruisce incollando tra loro due facce, quella rivolta al polo nord celeste e quella rivolta al polo sud. Entrambe le facce portano la scala dell’ascensione retta in ore. La faccia a nord porta la scala graduata in senso antiorario mentre la faccia a sud ha una scala che cresce in senso orario. Incollando le due parti bisogna prestare attenzione per far coincidere tra loro i valori delle due scale.

Le quattro scanalature interne servono per incastrare i due coluri i quali possiedono delle corrispondenti scanalature esterne. Il coluro degli equinozi si infilerà in corrispondenza delle scanalature posizionate sulle $24^h=0^h$ (punto vernale) e sulle $12^h$ (primo punto della Bilancia). Il coluro dei solstizi si incastrerà sulle due scanalature rimanenti $(6^h$ e $18^h)$.

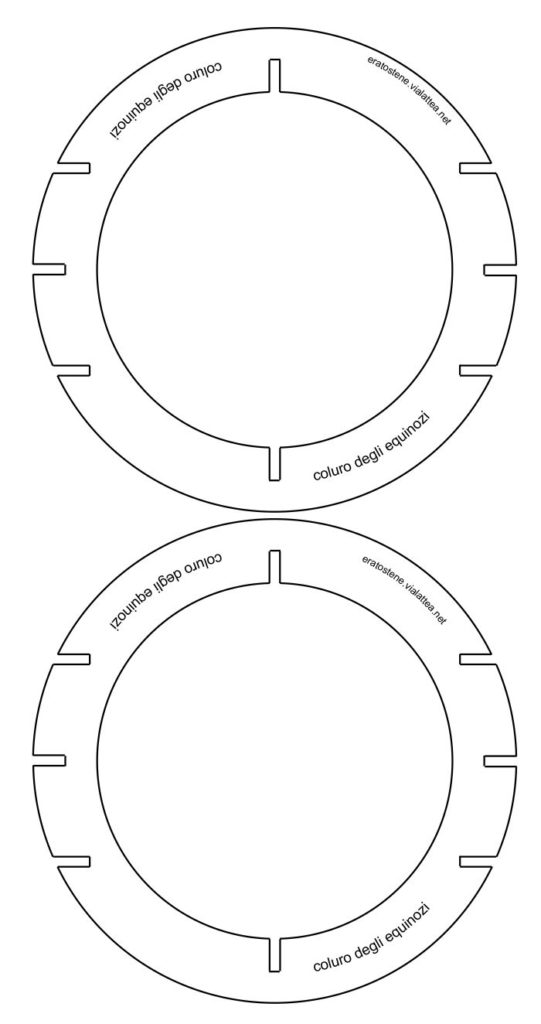
I due anelli del coluro degli equinozi vanno incollati assieme e le posizioni delle scanalature, che devono coincidere tra loro, guidano al corretto posizionamento.

Le due scanalature vericali interne permettono l’incastro con due scanalature esterne corrispondenti nel coluro dei solstizi.

Delle sei scanalature orizzontali, quelle centrali servono per l’incastro con l’equatore nei punti di ascensione retta $6^h$ e $18^h$.

Le altre due servono per l’incastro dei due tropici.

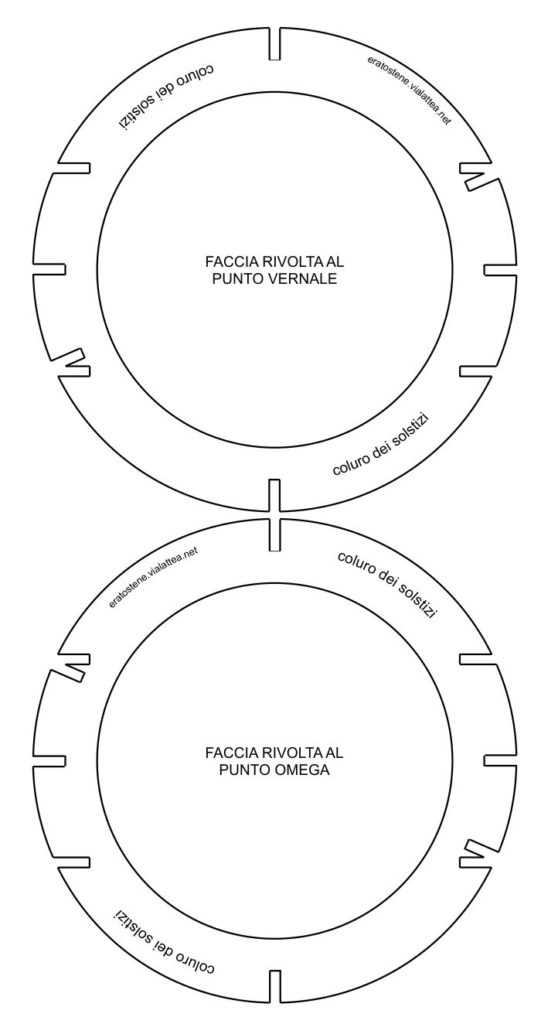
Il coluro dei solstizi è orientato. Oltre alle sei scanalature presenti anche nel coluro degli equinozi e con le stesse funzioni, qui si aggiungono due scanalature oblique per l’incastro con i due archi dell’eclittica. Le scanalature oblique sono inclinate di $\text{23,4}^\circ$ rispetto a quelle dell’equatore (che qui sono orizzontali). Le facce incollate tra loro devono far corrispondere tutte le scanalature.

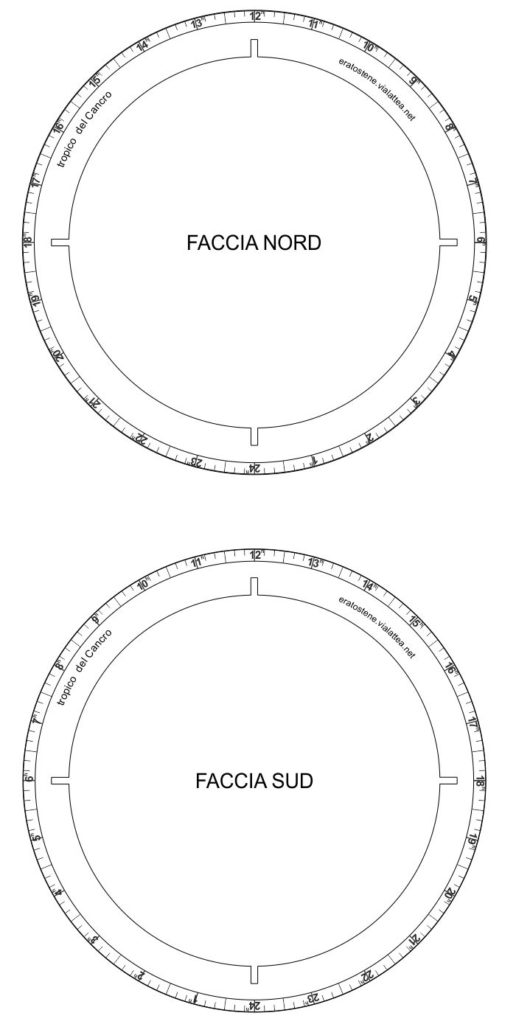
I tropici sono cerchi di dimensioni minori rispetto all’equatore. Il raggio dell’anello del tropico $r$ si ottiene dal raggio dell’equatore $R$ si ottiene da:

$$r=R\cdot\cos{\epsilon}$$

in cui $\epsilon$ è l’obliquità dell’eclittica $(\epsilon=\text{23,4}^\circ)$.

Il tropico del Cancro è il parallelo con declinazione $+\text{23,4}^\circ$ mentre il tropico del Capricorno ha decliazione $-\text{23,4}^\circ$.

Anche i tropici sono dotati delle scale di ascensione retta che devono essere orientate come quelle dell’equatore.

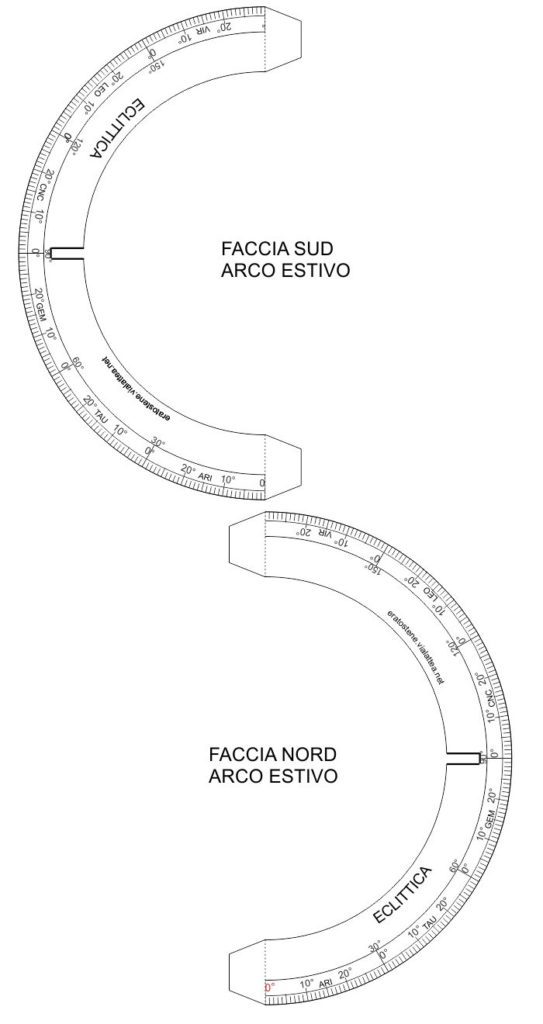
L’eclittica si costruisce in due semianelli: l’arco di declinazione positiva (“arco estivo”) e quello di declinazione negativa (“arco invernale”). Ciascuno di essi è composto di due facce da incolare tra loro. L’eclittica porta in evidenza una scala zodiacale. Le case dello zodiaco sono $12$ suddivisioni di $30^\circ$ ciascuna dell’eclittica. Ogni casa prende il nome di una costellazione dello zodiaco. La suddivisione in case zodiacali era un tradizionale metodo di conteggio della longitudine eclittica. Internamente alla scala zodiacale sono segnati anche i valori di longitudine, secondo il conteggio moderno, per ciascun primo punto delle case.

Le facce nord dell’eclittica hanno le scale in senso antiorario mentre per le facce sud è l’inverso.

Ogni semianello, una volta costruito incollando tra loro le due facce, andrà incollato alle intersezioni del coluro degli equinozi con l’equatore. Bisognerà prestare attenzione al fatto che lo zero $(24^h)$ della scala di ascensione retta presente sull’equatore deve corrispondere al primo punto dell’Ariete della scala zodiacale (longitudine $0^\circ$) mentre l’ascensione retta $12^h$ deve corrispondere al primo punto della Bilancia della scala zodiacale $(180^\circ$ di logitudine).

Le loro scanalature interne servono per l’incastro con le scanalature esterne inclinate di $\text{23,4}^\circ$ presenti sul coluro dei solstizi.