Le ore ineguali
Nell’antichità si dividevano le ore di luce (dall’alba al tramonto) in $12$ intervalli uguali chiamati ore ineguali, temporarie o anche antiche. Ne consegue che la loro durata cambiava di gorno in giorno: avevano una durata massima al solstizio di giugno e minima al solstizio di dicembre. Gli unici giorni dell’anno in cui le ore ineguali erano identiche alle ore solari erano i due equinozi. Vediamo ora come costruire una meridiana a ore ineguali.
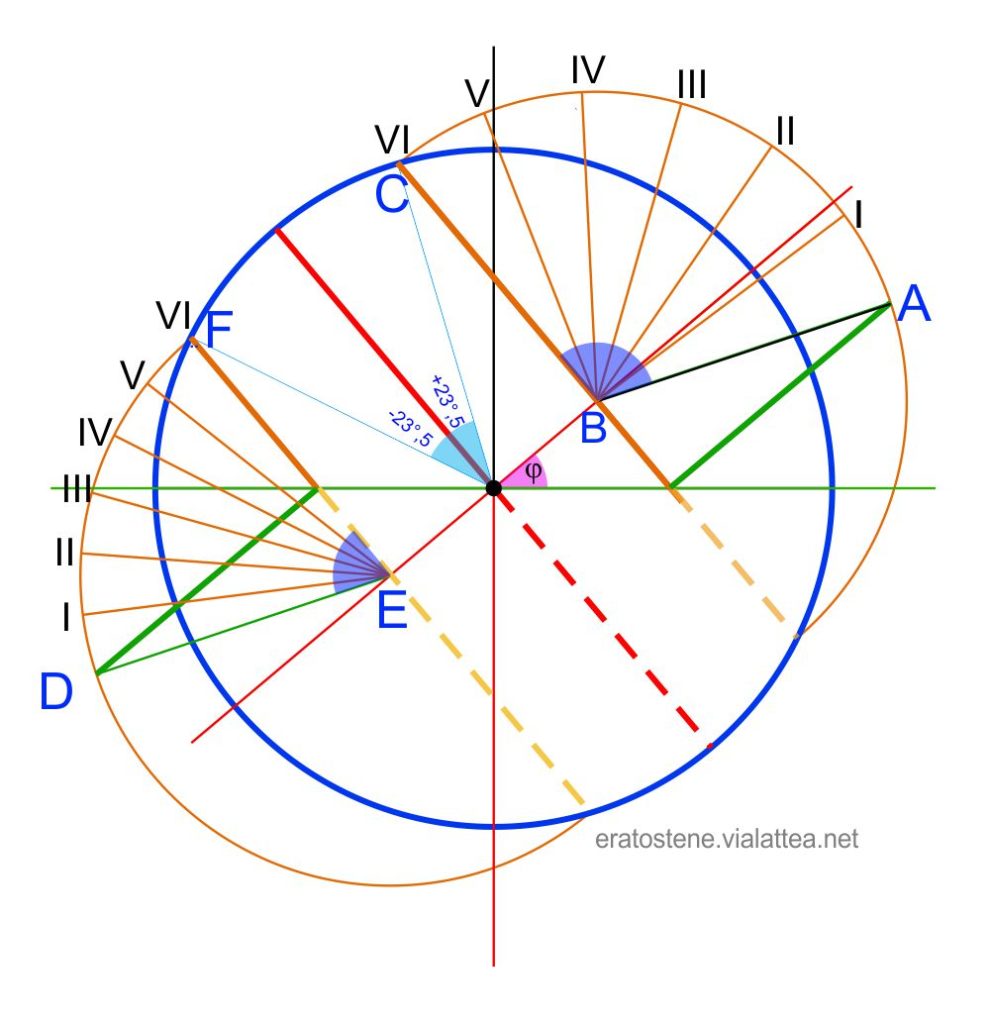
Prendiamo come esempio i paralleli di declinazione dei due solstizi. Al solstizio di giugno l’arco diurno del Sole è rappresentato dall’arco $AC$ sul circolo estivo. L’angolo $A\hat{B}C$ per questa latitudine misura $111^\circ\!,\!5$ e rappresenta la differenza di angolo orario tra l’alba (inizio del giorno) e il mezzogiorno (VI ora), oppure tra il mezzogiorno e il tramonto (XII ora). Se lo dividiamo in $6$ parti uguali otteniamo $6$ ore ineguali di $18^\circ\!,\!6$ ciascuna.
Analogamente, l’angolo $D\hat{E}F$ è la differenza di angolo orario tra l’alba e il mezzogiorno oppure tra il mezzogiorno e il tramonto nel giorno del solstizio di dicembre. Lo dividiamo in $6$ parti uguali e otteniamo le ore ineguali di $11^\circ\!,\!4$ ciascuna.
Utilizzando queste suddivisioni otteniamo un quadrante solare a ore ineguali.