La suddivisione dei circoli orari
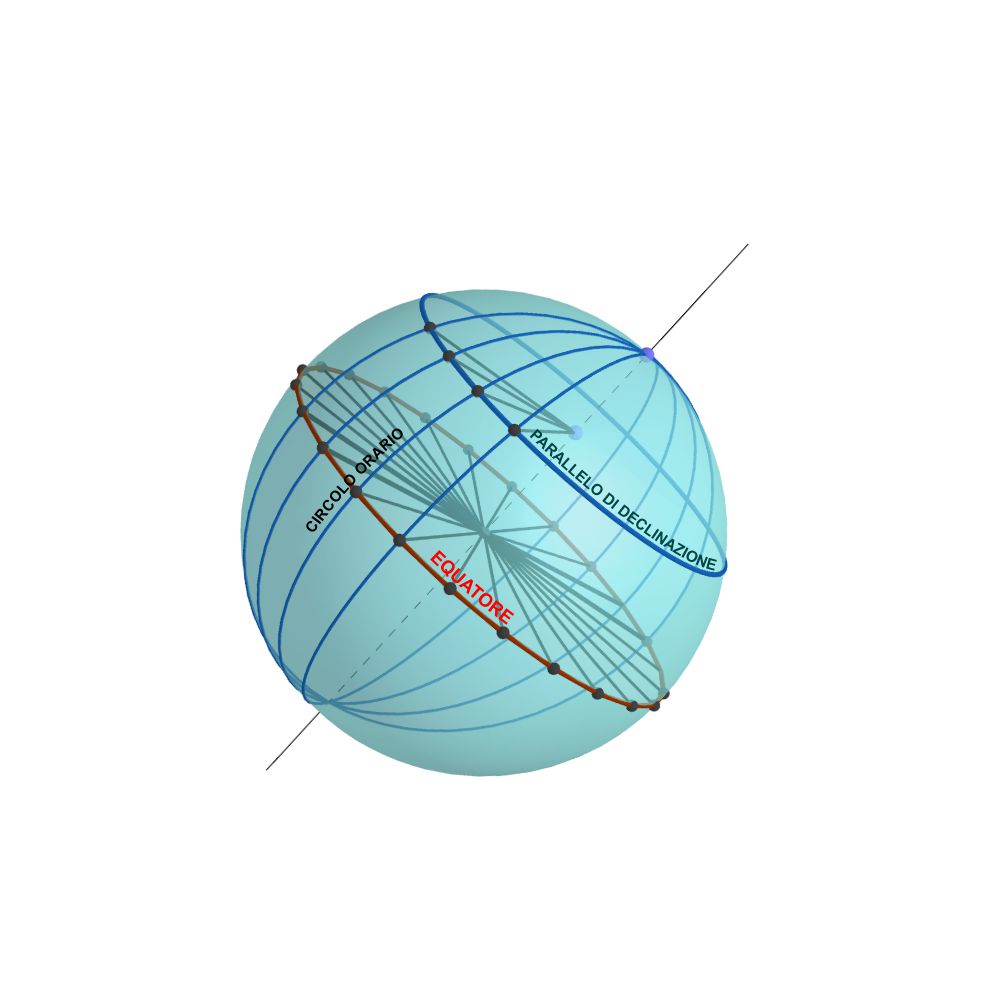
Immaginiamo di disegnare $12$ circoli orari distanziati di $15^\circ$. I piani di questi circoli orari suddividono sia l’equatore che un qualsiasi parallelo di declinazione in $24$ settori uguali di $15^\circ$ di ampiezza. Questa idea ci suggerisce la possibilità di suddividere un qualsiasi parallelo di declinazione del Sole in $24$ parti uguali che corrispondono a $24$ angoli orari di un’ora ciascuno e che rappresentano le posizioni del Sole per ogni ora del giorno.
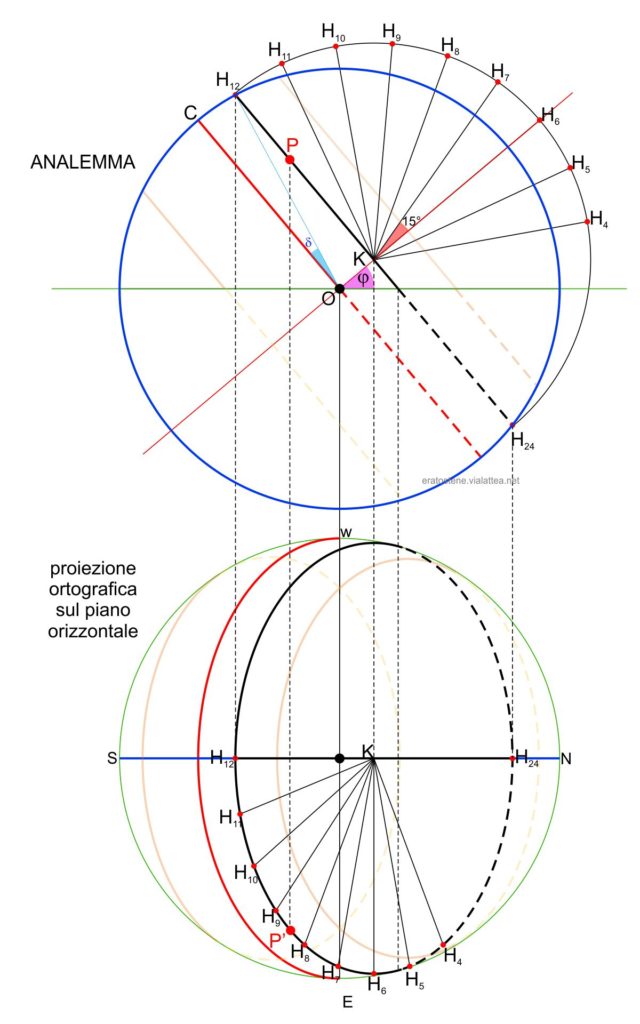
Il parallelo di declinazione che passa per il punto $P$ è il percorso apparente diurno del Sole in una certa data dell’anno, quando la sua declinazione è $\delta$. I due estremi del parallelo di declinazione $H_{12}$ e $H_{24}$ sull’analemma sono i punti in cui si trova il Sole rispettivamente al suo passaggio al meridiano superiore (mezzogiorno) e al suo passaggio al meridiano inferiore (mezzanotte).
Immaginiamo di ribaltare la semiconferenza orientale del parallelo di declinazione di $90^\1circ$ attorno al diametro $H_{12}H_{24}$ e la rappresentiamo disegnata sul piano dell’analemma. La suddividiamo in alcuni settori di $15^\circ$ ciascuno. I segmenti $KH_{12}$, $KH_{11}$, eccetera, sono archi di circoli orari: dato che il semicerchio del parallelo di declinazione è disegnato sul piano, essi sono rappresentati come segmenti. Ne disegniamo alcuni, corrispondenti alle ore del mattino, a cominciare dal cerchio orario delle ore $4$ fino a quello delle ore $12$. Questa scelta è dovuta al fatto che ci interessano le ore diurne a cominciare dall’alba. Non sappiamo ancora quando sorgerà il Sole, ma lo scopriremo presto. Nel frattempo, osservando la proiezione ortografica orizzontale, sarà facile intuire che l’alba avviene in qualche momento tra le $5$ e le $6$…
Osserviamo che il punto $P$, nella proiezione ortografica orizzontale, deve trovarsi in un punto $P’$ appartenente al parallelo di declinazione che in questo caso deve essere rappresentato come un’ellisse.

