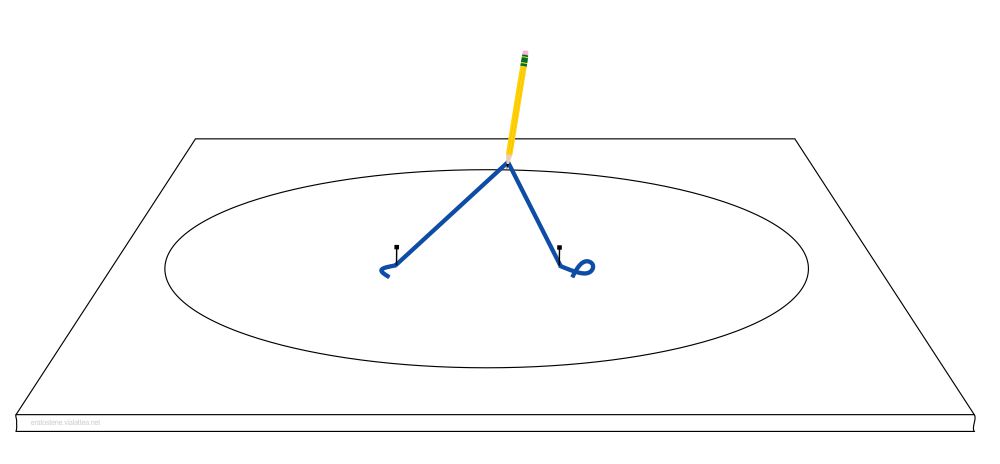
Si può facilmente disegnare un’ellisse usando una cordicella, due chiodini e una matita. Si stende il foglio su un piano di legno, si piantano i due chiodini e si legano ad essi i due capi della cordicella. Quindi si traccia una curva girando attorno ai chiodini, avendo cura di mantenere sempre in tensione la cordicella la quale limiterà il movimento della matita.
Questa costruzione dell’ellisse è interessante perché contiene la sua definizione.
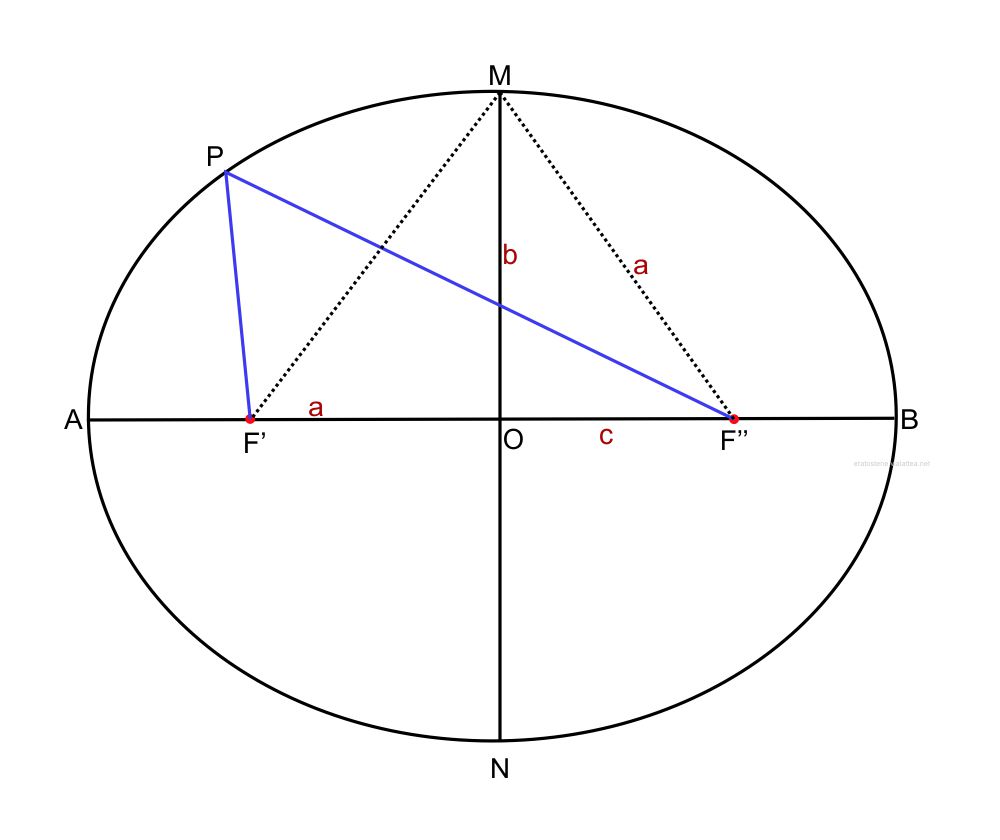
Infatti l’ellisse è una curva i cui punti rispettano la seguente legge: fissati due punti chiamati fuochi, la somma delle distanze tra un qualsiasi punto dell’ellisse e i fuochi è un valore costante (questa somma è la lunghezza della cordicella).
L’ellisse ha una forma di cerchio “schiacciato” e perciò non possiede un diametro ma un asse maggiore $AB$ e un asse minore $MN$. Chiameremo $a$ e $b$ le lunghezze del semiasse maggiore e del semiasse minore rispettivamente. L’intersezione degli assi è il punto $O$, chiamato centro dell’ellisse. I due fuochi $F’$ e $F^{”}$ si trovano sempre sull’asse maggiore e in posizioni simmetriche rispetto al centro. La lunghezza della cordicella corrisponde alla somma $PF’+PF ^{”}$ che per definizione deve essere costante. Tale lunghezza è uguale all’asse maggiore, $2a$, dell’ellisse. Lo si capisce facilmente portando la matita nel punto $A$; in questa posizione la cordicella è composta dai due tratti $AF^{”} $ e $AF’$ e quindi avremo:
$$AF^{”} +AF’=AF^{”} +BF^{”} =AB=2a$$
Se si porta la matita nel punto $M$ le due distanze $MF’$ e $MF^{”} $ diventano uguali tra loro e quindi uguali al semiasse maggiore $a$. Chiamiamo $c$ la distanza tra un fuoco e il centro dell’ellisse e costruiamo il triangolo rettangolo $MOF^{”} $ retto in $O$. L’ipotenusa è il semiasse maggiore $a$ e i cateti sono il semiasse minore $b$ e la distanza $c$.
Si definisce eccentricità dell’ellisse $e$ il rapporto:
$$e=\frac{c}{a}$$
Essendo $c=\sqrt{a^2-b^2}$, si può scrivere $e$ in funzione dei semiassi:
$$e=\frac{\sqrt{a^2-b^2}}{a}$$ oppure $$e=\sqrt{1- \left( \frac{b}{a} \right)^2}$$
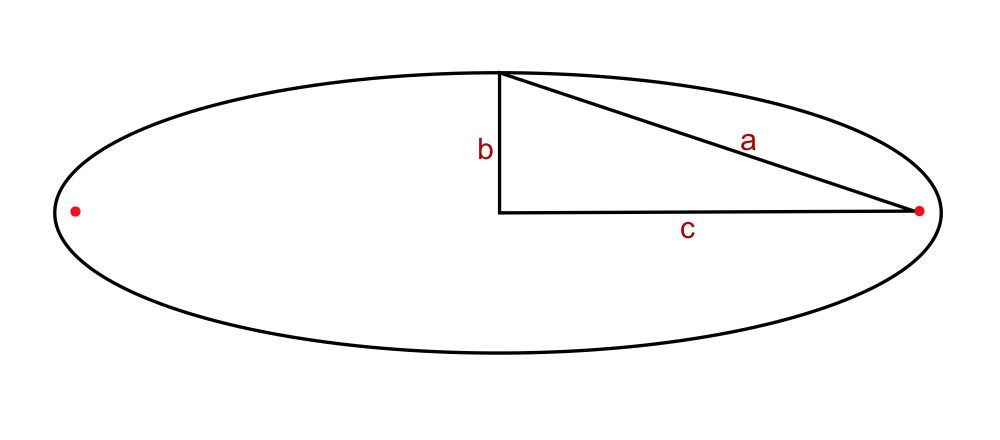
L’eccenticità $e$ è un valore compreso tra 0 e 1 e indica il “grado di schiacciamento” dell’ellisse. Il cateto $c$ non può mai essere maggiore dell’ipotenusa $a$ ma, se si allontanano tra loro i fuochi, tende ad essere uguale ad $a$.
Quindi, se la distanza tra i fuochi è di poco inferiore alla lunghezza della cordicella, l’ellisse è molto schiacciata e la sua eccentricità $e$ si avvicina al valore 1.
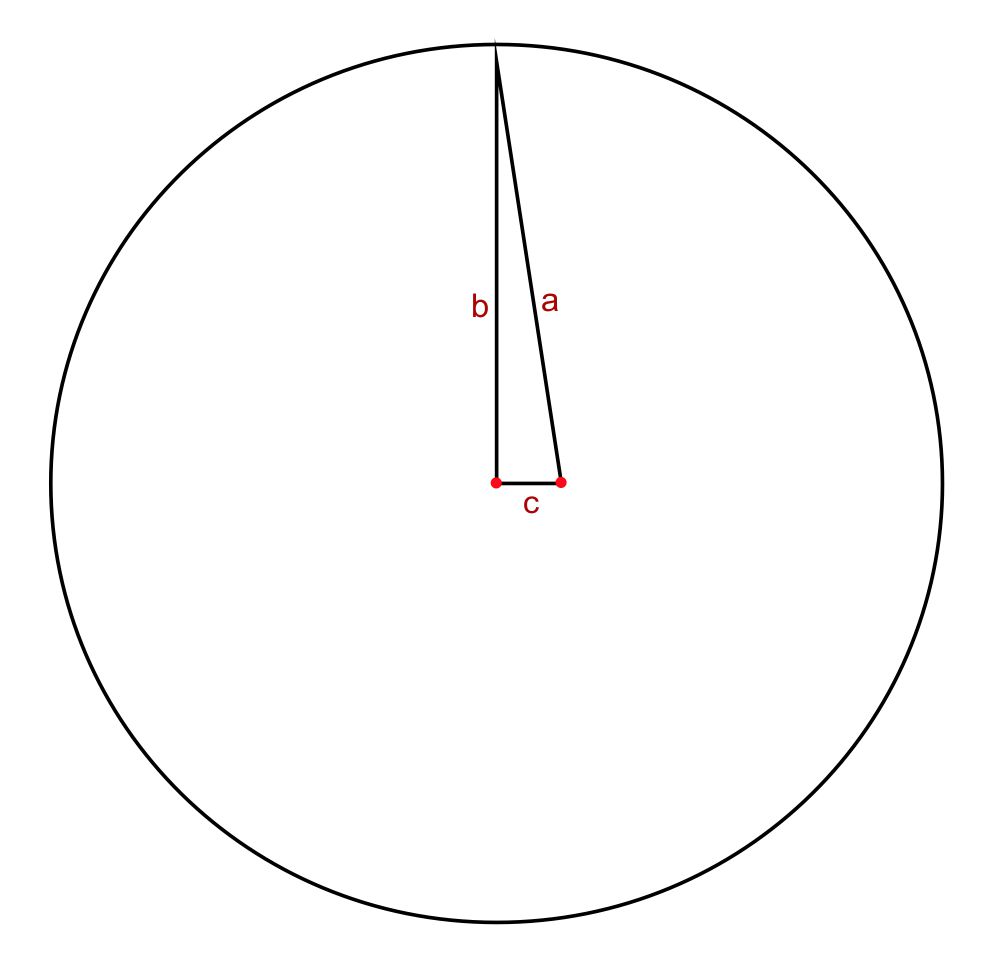
Se invece la distanza tra i fuochi è molto piccola rispetto alla lunghezza della cordicella, il semiasse maggiore $a$ è poco più grande del semiasse minore $b$; ne risulta un’ellisse molto poco schiacciata, che tende ad assomigliare ad un cerchio e il valore dell’eccentricità si avvicina allo zero.
L’eccentricità dell’orbita terrestre è attualmente 0,0167, relativamente piccola rispetto a quella degli altri pianeti. Il pianeta con maggiore eccentricità è Mercurio (0,2056) mentre Nettuno possiede il valore minimo (0,0097). L’eccentricità dei pianeti subisce piccole variazioni nel tempo, dovute all’attrazione gravitazionale reciproca.
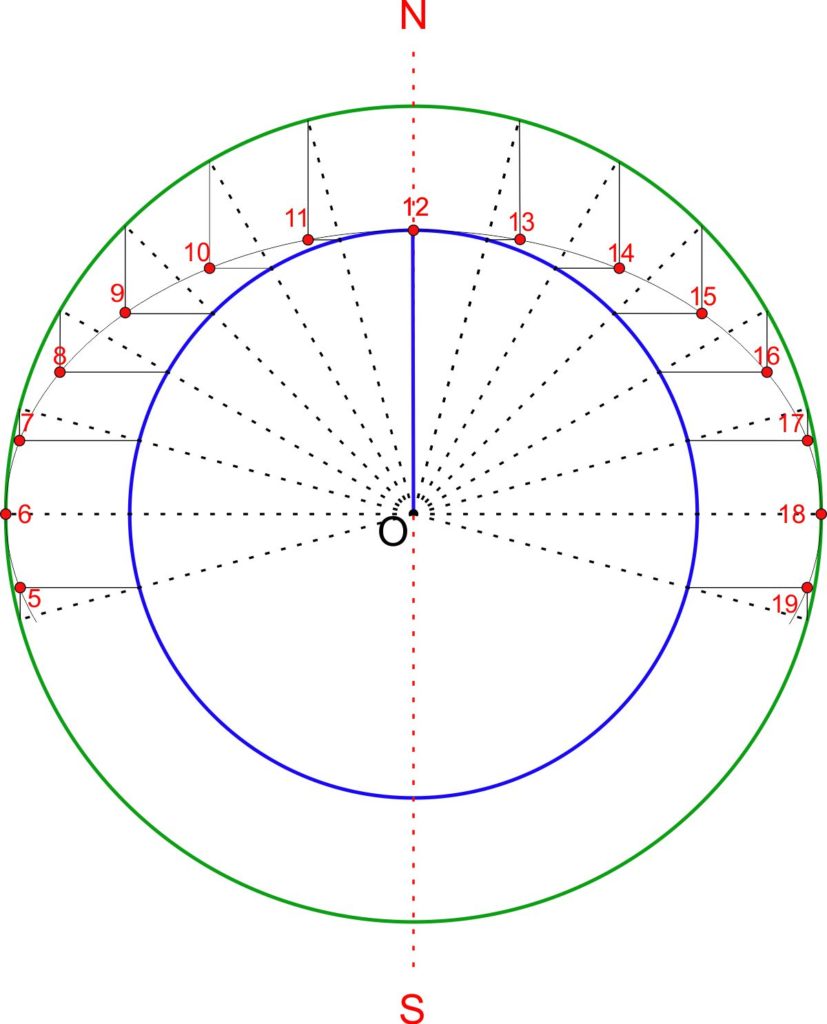
Un metodo grafico per disegnare un’ellisse è descritto nella pagina relativa alla costruzione di un orologio solare analemmatico. Si tratta di disegnare due cerchi concentrici i cui diametri sono uguali rispettivamente all’asse maggiore e all’asse minore dell’ellisse. Per trovare un punto dell’ellisse, si traccia un raggio e dai punti di intesezioni del raggio con le due circonferenze si disegnano una retta parallela all’asse maggiore dell’ellisse e un’altra perpendicolare. L’incrocio di queste due ultime rette è un punto dell’ellisse.
L’ellisse si ottiene anche come proiezione ortografica di un cerchio non parallelo al piano di proiezione. Ad esempio, nel diagramma orario, l’eclittica è rappresentata come un’ellisse.
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

