- Coordinate cartesiane o rettangolari
- Elementi di base delle coordinate sferiche
- Coordinate sferiche in astronomia
- Coordinate sferiche polari
- Coordinate sferiche ortogonali
- Conversione tra coordinate sferiche polari e rettangolari
- Trasformazione generale di coordinate sferiche
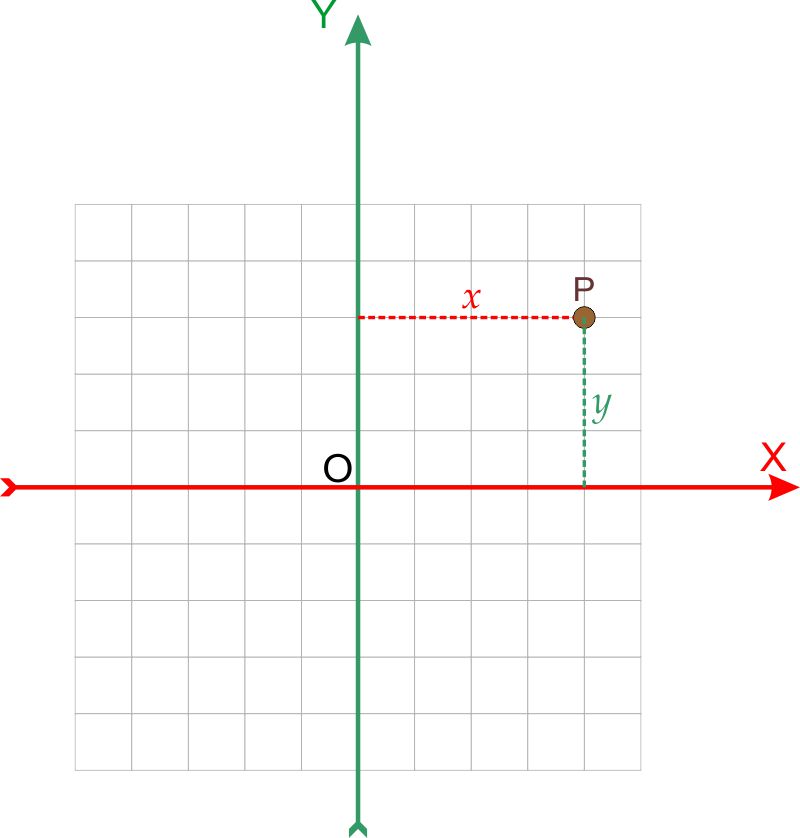
Il piano cartesiano è definito da due rette orientate e perpendicolari tra loro, chiamate assi cartesiani $X$ e $Y$ che si intersecano nel loro punto di origine $O$. La posizione di un punto $P$ nel piano può così essere identificata da due valori: l’ascissa $x$ che è la distanza tra il punto e l’asse Y e l’ordinata $y$ che è la distanza tra il punto e l’asse $X$. Per indicare la posizione di $P$ si scrive la coppia di coordinate:
$$P(x,y)$$
L’ascissa $x$ assume valori positivi se il punto $P$ si trova, come nell’esempio, a destra dell’asse $Y$ o negativi se il punto $P$ si trova a sinistra. L’ordinata $y$ assume valori positivi se il punto si trova al di sopra dell’asse $X$ e negativi se si trova al di sotto di esso.
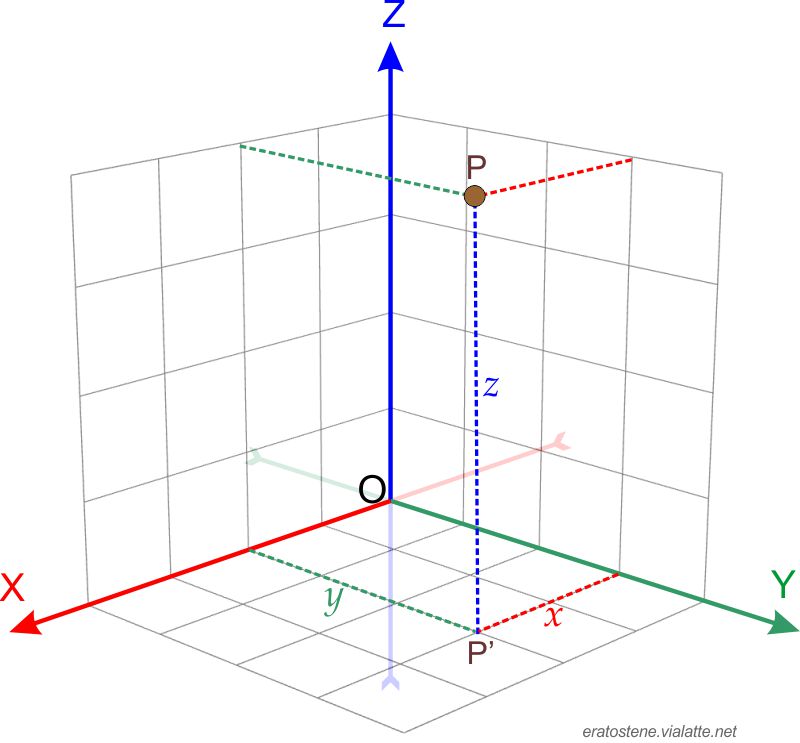
Le coordinate cartesiane nello spazio sono un’estensione del piano cartesiano per mezzo dell’aggiunta di un terzo asse $Z$ perpendicolare ad esso.
Per identificare la posizione di un punto $P$ nello spazio a tre dimensioni si misurano perciò tre distanze:
- coordinata $\boldsymbol{x}$, chiamata anche ascissa, che rappresenta la distanza tra il punto $P$ e il piano $YZ$;
- coordinata $\boldsymbol{y}$, chiamata anche ordinata, che è la distanza tra il punto $P$ e il piano $XZ$;
- coordinata $\boldsymbol{z}$, chiamata anche quota del punto $P$, che è la distanza tra il punto $P$ dal piano $XY$.
In questo modo la posizione del punto $P$ può essere definita così:
$P(x,y,z)$
In questa rappresentazione dello spazio cartesiano, per ragioni di semplicità, si sono trascurati i settori con valori negativi delle coordinate. Se il punto si trova “dietro” al piano $YZ$ della nostra rappresentazione, la coordinata $x$ è sempre negativa, “dietro” al piano $XZ$ la coordinata $y$ è negativa e “sotto” il piano $XY$ sono i valori di $z$ ad essere sempre negativi.
In astronomia, questo sistema di coordinate è spesso chiamato sistema di coordinate rettangolari, per distinguerlo dai sistemi di coordinate sferiche.

