In questa pagina si descrive uno dei metodi generici di trasformazione di coordinate sferiche di un astro da un sistema di riferimento ad un altro. L’esempio riguarda le coordinate polari, ma con un metodo analogo, che si basa sempre sull’applicazione delle leggi del triangolo sferico, si può ottenere la trasformazione di coordinate sferiche ortogonali. Nell’applicare questi metodi alle trasformazioni di coordinate astronomiche abbiamo il vantaggio di alcune semplificazioni dovute al fatto che i loro sistemi di riferimento sppesso condividono tra loro uno o più elementi. Ad esempio, il sistema orario e il sistema altazimutale condividono lo stesso cerchio fondamentale (il meridiano celeste). Un altro esempio è dato dai sistemi equatoriale ed eclittico che condividono il coluro dei solstizi.
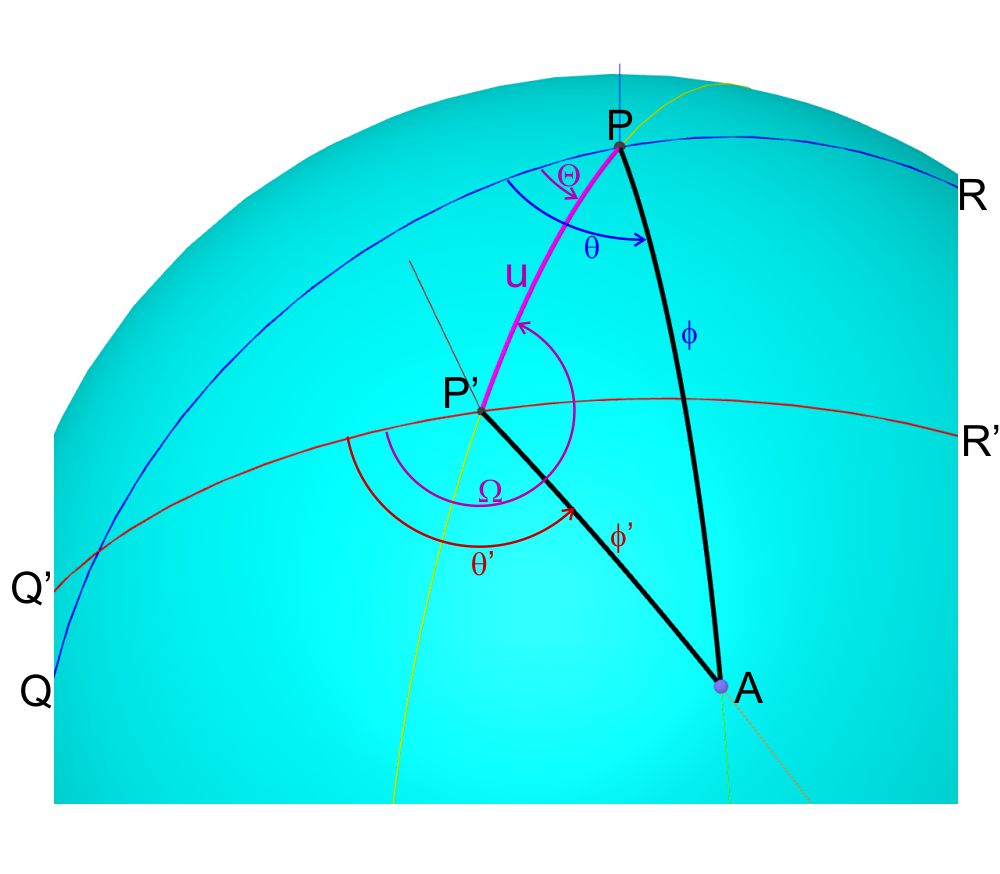
In questa immagine:
- $A$ è la posizione di un astro
- $P$ è il polo del sistema di riferimento originario di cui si conoscono le coordinate dell’astro $A$.
- $P’$ è il polo del nuovo sistema di cui si intende calcolare le coordinate.
- L’arco $QPR$ è il circolo fondamentale del primo sistema.
- L’arco $Q’P’R’$ è il circolo fondamentale del secondo sistema.
- L’angolo sferico $\theta=Q\hat PA$ e l’arco di cerchio massimo $\phi=PA$ sono le coordinate polari note dell’astro $A$, riferite al primo sistema.
- L’angolo sferico $\theta’=Q’\widehat{P’}A’$ e l’arco di cerchio massimo $\phi’=P’A’$ sono le coordinate polari dell’astro $A$, riferite al secondo sistema, quelle che intendiamo calcolare.
Gli elementi che mettono il relazione tra loro il primo e il secondo sistema di riferimento sono:
- L’angolo sferico $\Theta=Q\hat PP’$ e l’arco di cerchio massimo $u$ che sono le coordinate del polo $P’$ rispetto al primo sistema di riferimento che ha per polo il punto $P$.
- L’angolo sferico $\Omega$ definisce l’assetto del circolo fondamentale $Q’P’R’$ del secondo sistema. Ricordiamo che il circolo fondamentale definisce l’origine dell’azimut di sistema di riferimento polare.
Il triangolo $APP’$ è un triangolo sferico perché i suoi lati sono archi di cerchio massimo e perciò possiamo applicare ad esso le formule fondamentali di trigonometria sferica che riportiamo qui:
\begin{align*}
\cos{a}&=\cos{b}\cdot\cos{c}+\sin{b}\cdot\sin{c}\cdot\cos{\alpha} \\
\sin a\cdot\sin \beta &=\sin{\alpha}\cdot\sin{b}\\
\sin a \cdot \cos \beta &= \cos b \cdot \sin c – \sin b\cdot\cos c \cdot \cos \alpha
\end{align*}

Sostituiamo gli elementi delle formule generiche con i corrispondenti elementi delle coordinate definiti prima:
$a=\phi’$
$b=\phi$
$\alpha=\Theta-theta$
$\beta=\Omega-\theta’$
$c=u$
Si ottengono le seguenti uguaglianze:
\begin{equation}\tag{1}\label{eq1}
\cos{\phi’}=\cos{\phi}\cdot\cos{u}+\sin{\phi}\cdot\sin{u}\cdot\cos{(\Theta-\theta)}
\end{equation}
\begin{equation}\tag{2}\label{eq2}
\sin{\phi’}\cdot \sin{(\Omega-\theta’)}= \sin{\phi} \cdot \sin{(\Theta-\theta)}
\end{equation}
\begin{equation}\tag{3}\label{eq3}
\sin \phi’ \cdot \cos (\Omega-\theta’) = \cos \phi \cdot \sin u – \sin \phi\cdot\cos u \cdot \cos (\Theta-\theta)
\end{equation}
La (1) si può utilizzare tale e quale: essa permette di calcolare la nuova colatitudine $\phi’$ in base alle coordinate del primo sistema.
Ora dividiamo membro a membro la (2) e la (3) ottenendo:
$$\frac{\sin{\phi’}\cdot \sin{(\Omega-\theta’)}}{\sin \phi’ \cdot \cos (\Omega-\theta’)}=\frac{\cos \phi \cdot \sin u – \sin \phi\cdot\cos u \cdot \cos (\Theta-\theta)}{\sin{\phi} \cdot \sin{(\Theta-\theta)}}$$
da cui, semplificando:
$$\tan (\Omega-\theta’)=\frac{\cos \phi \cdot \sin u – \sin \phi\cdot\cos u \cdot \cos (\Theta-\theta)}{\sin{\phi} \cdot \sin{(\Theta-\theta)}}$$
che permette di calcolare il nuovo l’azimut $\theta’$ in funzione delle coordinate del primo sistema di riferimento.

