- Coordinate cartesiane o rettangolari
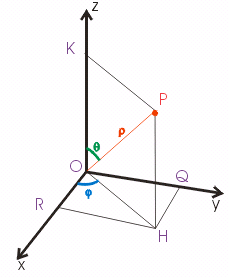
- Elementi di base delle coordinate sferiche
- Coordinate sferiche in astronomia
- Coordinate sferiche polari
- Coordinate sferiche ortogonali
- Conversione tra coordinate sferiche polari e rettangolari
- Trasformazione generale di coordinate sferiche
Un punto P è individuato dalla terna ![]() ,
, ![]() e
e ![]() dove:
dove:
![]() è chiamato raggio vettore (distanza PO)
è chiamato raggio vettore (distanza PO)
![]() è chiamato distanza zenitale o colatitudine (angolo formato da PO con l’asse z, dove O è l’origine degli assi)
è chiamato distanza zenitale o colatitudine (angolo formato da PO con l’asse z, dove O è l’origine degli assi)
![]() si chiama azimut o longitudine (angolo formato da OH con l’asse x dove H è la proiezione ortogonale del punto P sul piano xy).
si chiama azimut o longitudine (angolo formato da OH con l’asse x dove H è la proiezione ortogonale del punto P sul piano xy).
Lo stesso punto P si può individuare utilizzando anche una terna di coordinate cartesiane rettangolari (x, y e z).
Per passare dalle coordinate polari a quelle rettangolari, cioè da una terna (![]() ,
, ![]() ,
, ![]() ) alla corrispondente terna (
) alla corrispondente terna (![]() ,
, ![]() ,
, ![]() ) si utilizzano le seguenti relazioni:
) si utilizzano le seguenti relazioni:
(1) ![]()
(2) ![]()
(3) ![]()
Viceversa, per ottenere le coordinate polari dalle rettangolari:
(4) ![]()
(5) ![]()
(6) 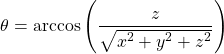


Può essere utile ricordare che mentre con le coordinate cartesiane ortogonali ogni punto dello spazio ha sempre una terna ordinata di coordinate e viceversa.
Altrettanto non succede le coordinata polari nello spazio. I punti sull’asse polare (abbinato usualmente con l’asse Z nel cambio coordinate) non hanno definita l’angolo azimut o longitudine o giacitura o attitude (anglofoni) tali punti hanno solo due coordinate ro, distanza da origine, e teta, distanza zenitale. Tranne il Polo O, che corrisonde con l’origine coordinate cartesiane che ha una sola coordinata polare ro=0. Questo di solito non crea problemi particolari a noi umani che intuiamo e gestiamo al volo le eccezioni, salvo si volesse scrivere un codice per calcolatore che sappia in ogni caso eseguire passaggj di coordinate e collocare cirrettamente i punti sulla sfera di rappresentazione.