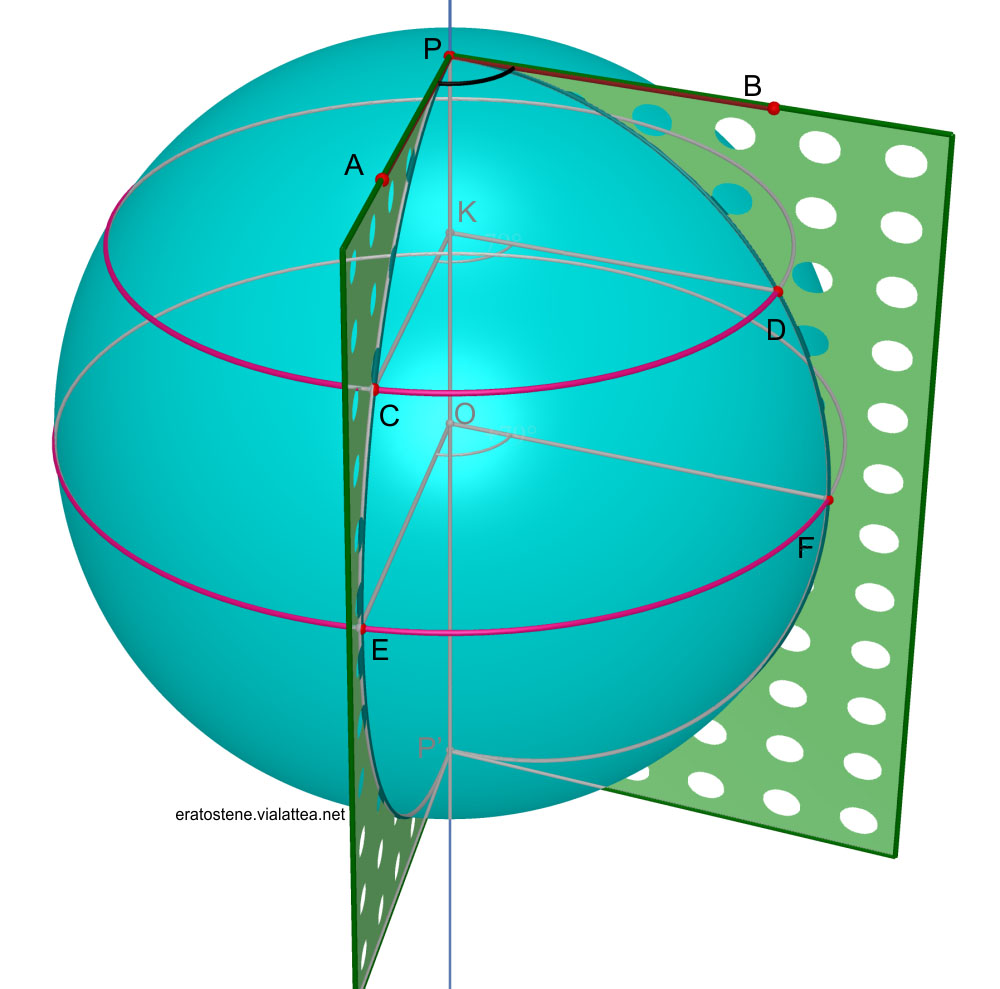
La sfera qui rappresentata ha il centro in $O$ e il segmento $PP’$ è un suo diametro. I due semicerchi $PCEP’$ e $PDFP’$ sono parti di cerchi massimi e appartengono a due semipiani che hanno come origine comune l’asse $PP’$. L’angolo sferico compreso tra i due semicerchi è l’angolo diedro (cioè l’angolo solido) compreso tra questi due semipiani.
Il diametro $PP’$ si chiama spigolo dell’angolo sferico. Il punto $P$ si chiama vertice dell’angolo sferico.
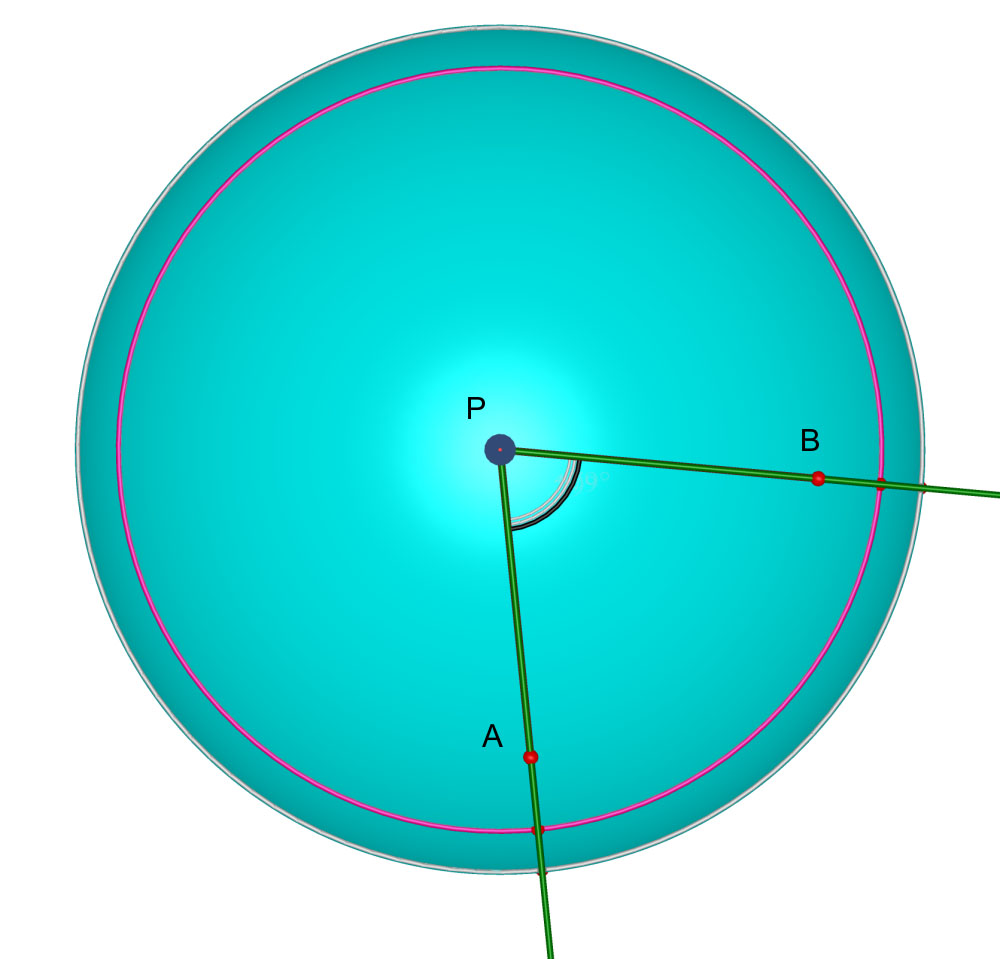
L’ampiezza dell’angolo sferico si misura attraverso l’angolo piano $\hat{APB}$ le cui semirette $AP$ e $BP$ sono tangenti ai rispettivi semicerchi nel loro punto in comune $P$.
L’angolo sferico qui definito e la sua ampiezza possono essere descritti in vari modi equivalenti:
- angolo $CPD$, i cui lati sono archi di cerchio massimo e il cui vertice è il punto $P$;
- angolo al centro $\hat{EOF}$ dove $O$ è il centro della sfera;
- arco di cerchio massimo $\overset{\frown}{EF}$.
- angolo $\hat{CKD}$, dove i lati $CK$ e $DK$ sono perpendicolari allo spigolo. E’ da notare che la lunghezza dell’arco $\overset{\frown}{CD}$ rappresentato in figura non è l’ampiezza dell’angolo sferico perché il cerchio cui appartiene è un cerchio minore.
~~~GLOSSARIO~~~

