I triangoli sferici rettangoli e rettilateri godono di particolari vantaggi essendo sempre nota una delle sei variabili. In questi casi sono utili le regole di Nepero che producono dieci formule per ciascun tipo di triangolo e che permettono di calcolare uno qualsiasi degli elementi del triangolo quando ne sono noti altri due. La difficoltà di consultare una tabella di dieci formule o, peggio ancora, di impararle a memoria, si risolve con dei trucchi mnemonici che descriviamo qui, basati su una sola regola e su due schemi grafici.

Triangolo sferico rettangolo

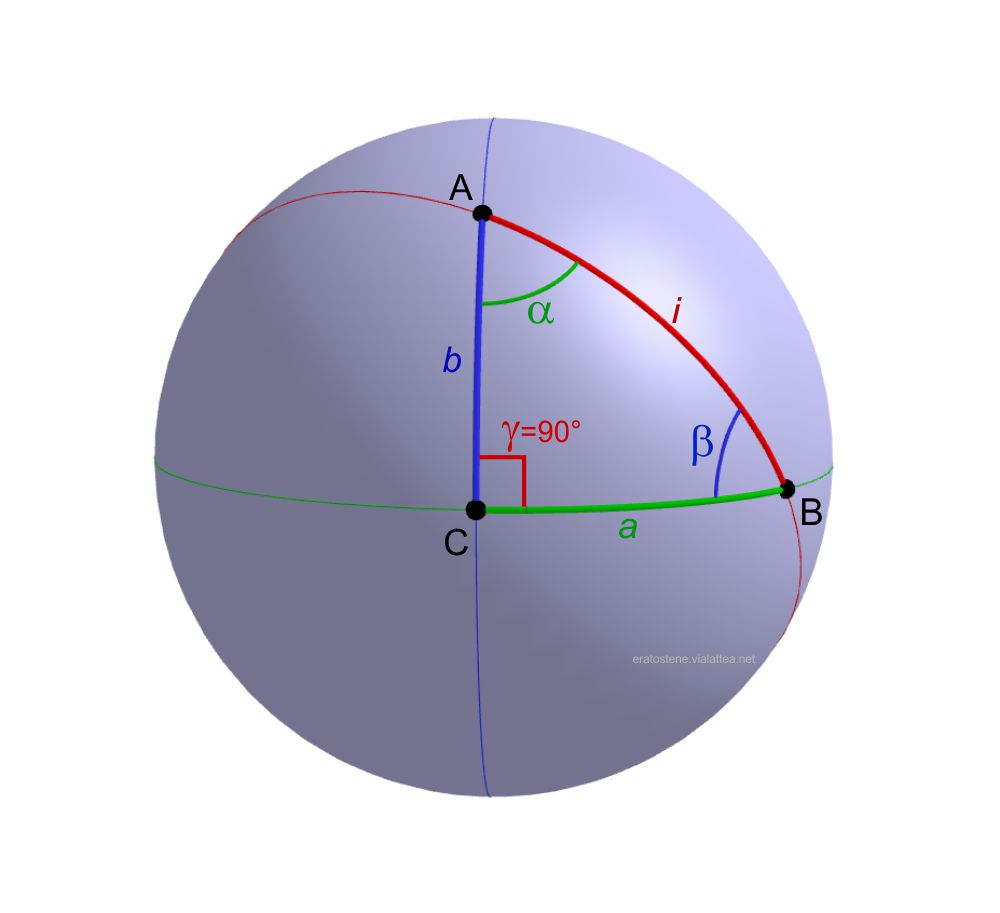
Il triangolo sferico rettangolo ha un angolo retto, in questo disegno $\gamma=90^\circ$. Chiamiamo $a$ e $b$ i due cateti, l’ipotenusa è il terzo lato $i$. Gli angoli $\alpha$ e $\beta$ sono i due angoli opposti rispettivamente al cateto $a$ e al cateto $b$.

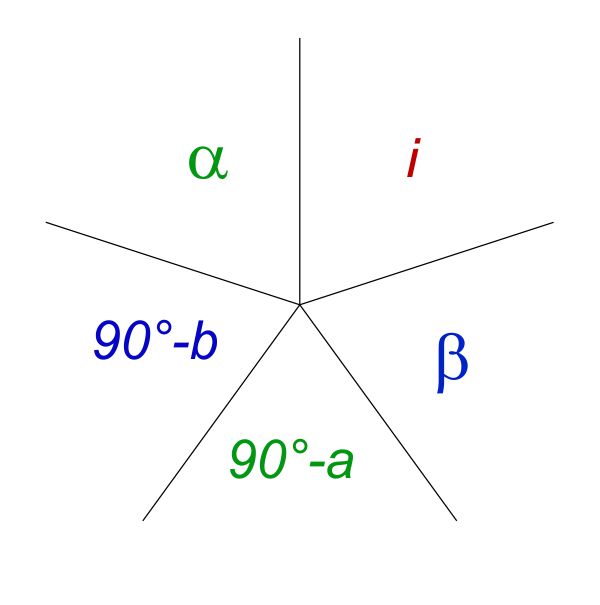
La regola di Nepero è facilmente memorizzabile. Si disegnano cinque settori a stella e si dispongono in senso orario o antiorario i cinque elementi del triangolo rettangolo sferico escludendo l’angolo $\gamma=90^\circ$. In questo caso sono stati disposti in senso orario. Bisogna però mettere al posto dei cateti i loro complementi.

La regola è la seguente: il coseno di uno dei cinque elementi è uguale al prodotto delle cotangenti degli elementi adiacenti oppure al prodotto dei seni degli elementi più lontani.

Come esempio, immaginiamo di dover calcolare l’angolo $\beta$.

Seguendo la prima parte della regola mnemonica si ottiene:

$$\cos{\beta}=\cot{i}\cdot\cot{(90^\circ-a)}$$

da cui si può scrivere (vedi trigonometria utile):

$$\boxed{\cos{\beta}=\cot{i}\cdot\tan{a}}$$

Seguendo la seconda parte della regola:

$$\cos{\beta}=\sin{\alpha}\cdot\sin{(90^\circ-b)}$$

che può essere trasformata in:

$$\boxed{\cos{\beta}=\sin{\alpha}\cdot\cos{b}}$$

Come secondo esempio immaginiamo di dover calcolare il lato $b$. Anche in questo caso abbiamo due possibilità:

$$\cos(90^\circ-b)=\cot\alpha\cdot\cot(90^\circ-a)$$

che si può scrivere:

$$\boxed{\sin b = \cot\alpha\cdot \tan a}$$

oppure:

$$\cos(90^\circ-b)=\sin i\cdot\sin \beta$$

che si può scrivere:

$$\boxed{\sin b = \sin i\cdot\sin \beta}$$

Triangolo sferico rettilatero

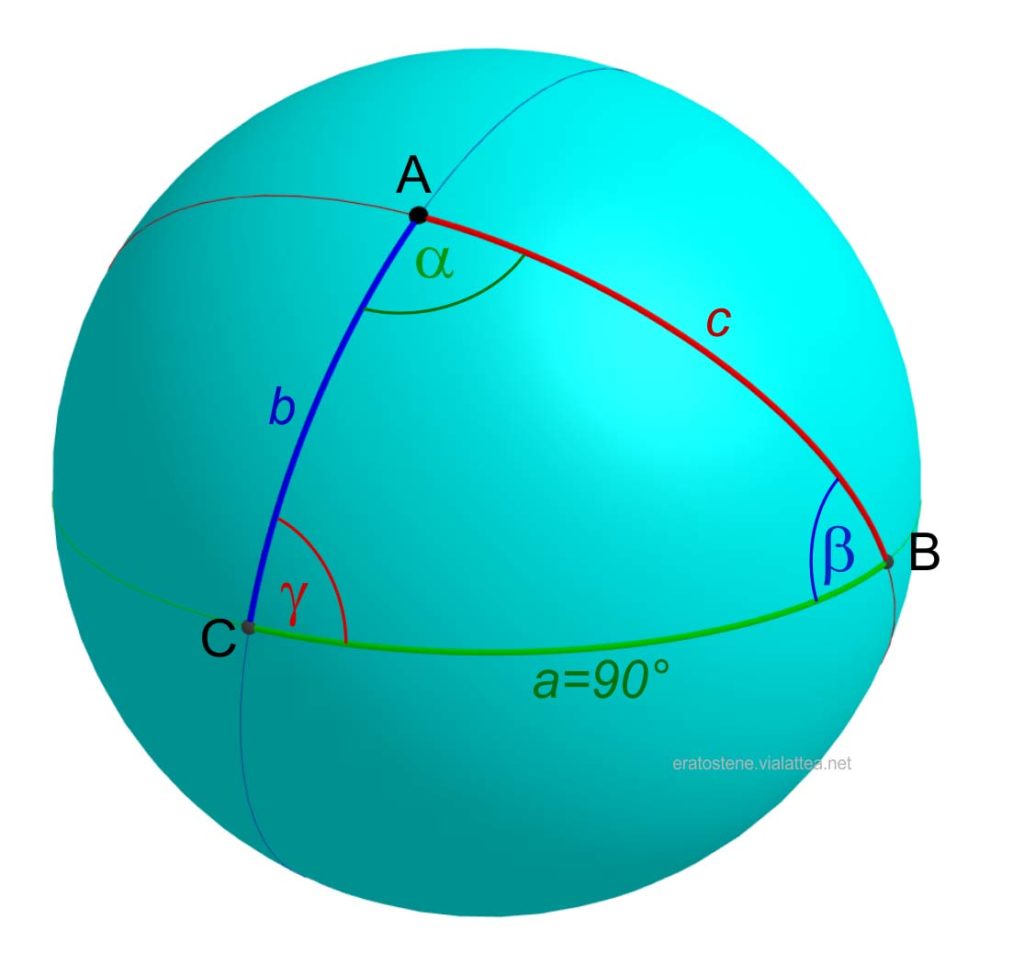
Il triangolo sferico rettilatero ha un lato di $90^\circ$. Nel disegno a fianco il lato $a=90^\circ$.

Anche in questo caso una regola mnemonica ci viene in aiuto se prima disponiamo i cinque elementi in ordine orario o antiorario, escludendo il lato retto, e mettendo al posto degli angoli adiacenti al lato retto ($\beta$ e $\gamma$) i loro complementari, e al posto dell’angolo opposto al lato retto ($\alpha$) il suo supplementare.

La regola è identica alla precedente: il coseno di uno dei cinque elementi è uguale al prodotto delle cotangenti degli elementi adiacenti oppure al prodotto dei seni degli elementi più lontani.

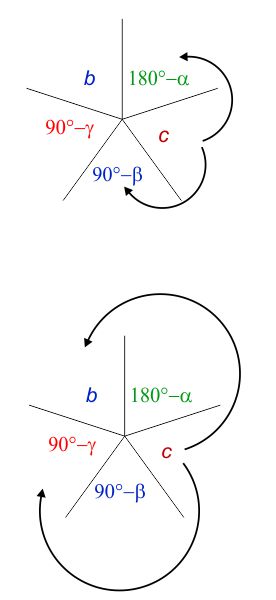
Come esempio applichiamo la regola per calcolare $\cos c$:

$$\cos c= \cot (180^\circ-\alpha)\cdot\cot(90^\circ-\beta)$$

che diventa (vedi trigonometria utile):

$$\boxed{\cos c= -\cot \alpha\cdot\tan\beta}$$

oppure:

$$\cos c = \sin b\cdot\sin(90^\circ-\gamma)$$

che si trasforma in:

$$\boxed{\cos c = \sin b\cdot\cos\gamma}$$