Seno, coseno e tangente

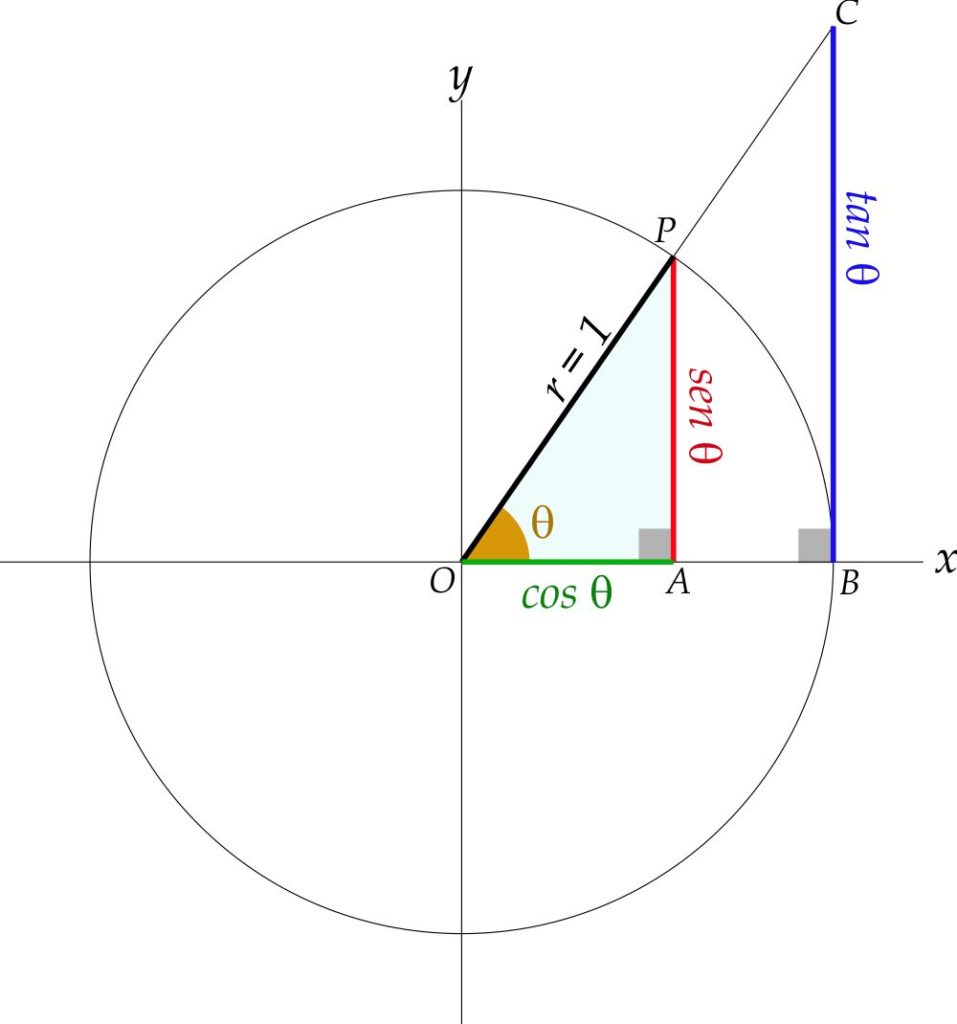
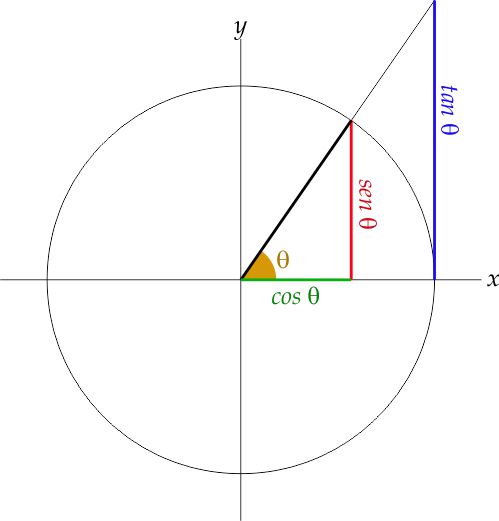
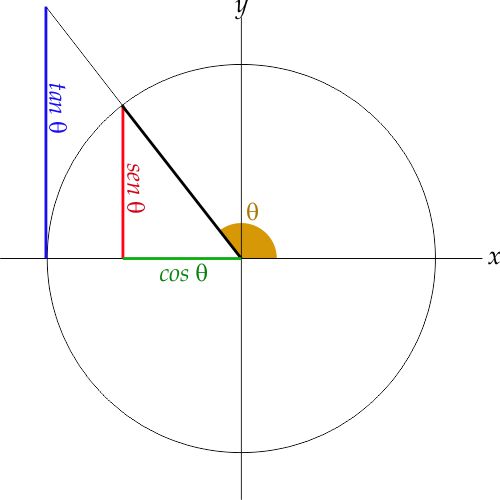
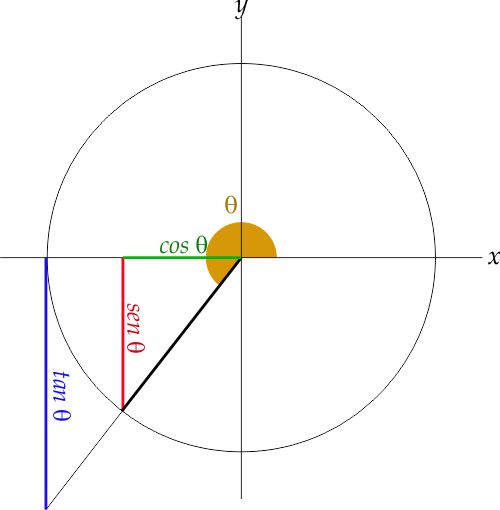
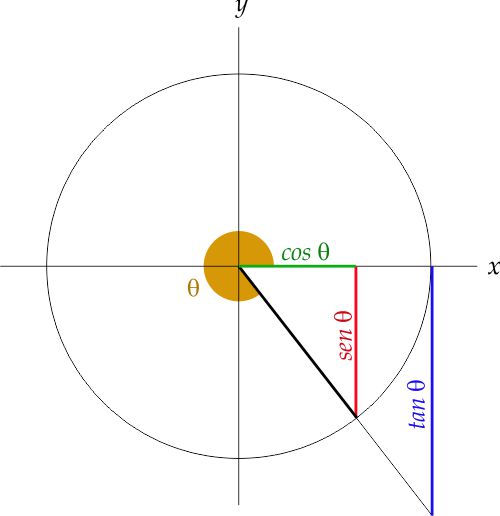
Le funzioni trigonometriche mettono in relazione le misure dei lati di un triangolo rettangolo con le ampiezze dei suoi angoli. Una circonferenza di raggio unitario $(OP=r=1)$ è disegnata con il suo centro $O$ all’origine degli assi cartesiani $x$ e $y$. Il punto P si trova su questa circonferenza e il raggio $OP$ forma l’angolo $\theta$ con l’asse $x$. Si consideri il triangolo rettangolo $OAP$, retto in $A$. Il cateto $OA$, adiacente all’angolo $\theta$, è il coseno di $\theta$ e la sua misura rappresenta anche l’ascissa del punto $P$. Il cateto $AP$, opposto all’angolo $\theta$ è il seno dello stesso angolo e la sua lunghezza è anche l’ordinata del punto $P$. Si consideri ora il triangolo rettangolo $OBC$, simile al triangolo $OAP$ retto in $B$. Il suo cateto $OB$ che si trova sull’asse $x$ è uguale al raggio $r$. Il cateto $BC$ è tangente alla circonferenza nel punto $B$. Per questo motivo la sua lunghezza è chiamata tangente dell’angolo $\theta$.

Le tre funzioni $\sin$ (o sen), $\cos$ e $\tan$ (o tg) sono chiamate funzioni dirette: dato il valore dell’angolo $\theta$ esse forniscono la lunghezza del loro segmento.

Le funzioni seno e coseno forniscono valori compresi tra $-1$ e $+1$ mentre la tangente fornisce valori compresi tra $-\infty$ e $+\infty$. Il segno dipende dall’ampiezza di $\theta$ che determina la posizione del punto $P$ nei vari quadranti:
QUADRANTE I
Coseno: $\LARGE+$
Seno: $\LARGE+$
Tangente: $\LARGE+$
QUADRANTE II
Coseno: $\LARGE-$
Seno: $\LARGE+$
Tangente: $\LARGE+$
QUADRANTE III
Coseno: $\LARGE-$
Seno: $\LARGE-$
Tangente: $\LARGE-$
QUADRANTE IV
Coseno: $\LARGE+$
Seno: $\LARGE-$
Tangente: $\LARGE-$

Arcoseno, arcocoseno e arcotangente

Le funzioni inverse, arcoseno, arcocoseno e arcotangente indicate rispettivamente con $\arcsin$, $\arccos$ e $\arctan$ oppure $\sin^{-1}$, $\cos^{-1}$ e $\tan^{-1}$,  restituiscono invece l’ampiezza dell’angolo $\theta$ se si conosce la lunghezza del segmento corrispondente.

Ad esempio:
$\sin 32^\circ = \text{0.5299}$
$\arcsin \text{0,5299}=32^\circ$

Secante, cosecante e cotangente

Accenniamo inoltre a tre funzione reciproche: la cotangente $(\cot)$ reciproca della tangente, la secante $(\sec)$ reciproca del coseno e la cosecante $(\csc)$ reciproca del seno:

$$\cot{\theta}=\frac{1}{\tan{\theta}}$$

$$\sec{\theta}=\frac{1}{\cos{\theta}}$$

$$\csc{\theta}=\frac{1}{\sin{\theta}}$$

Alcune formule utili

$$\sin{(90^\circ-\alpha)}=\cos{\alpha}$$

$$\cos{(90^\circ-\alpha)}=\sin{\alpha}$$

$$\tan{(90^\circ-\alpha)}=\cot{\alpha}$$

$$\cot{(90^\circ-\alpha)}=\tan{\alpha}$$

Il termine “seno” ha una curiosa storia etimologica. L’origine va cercata nella parola sanscrita jiva che significa corda. In realtà, jiva era una semplificazione di jiva-ardha, cioè mezza corda. La traslitterazione araba fujiba o jb che, essendo priva di significato , fu trasformata in jaib che vuol dire baia o rada. Infine, nel XII secolo, Gherardo da Cremona tradusse dall’arabo con il termine latino sinus (petto, cavità, insenatura).
Il termine “coseno” deriva dal latino co(mplementi) sinus, cioè seno dell’angolo complementare. Infatti, il coseno di $\alpha$ è uguale al seno di $90^\circ-\alpha$.