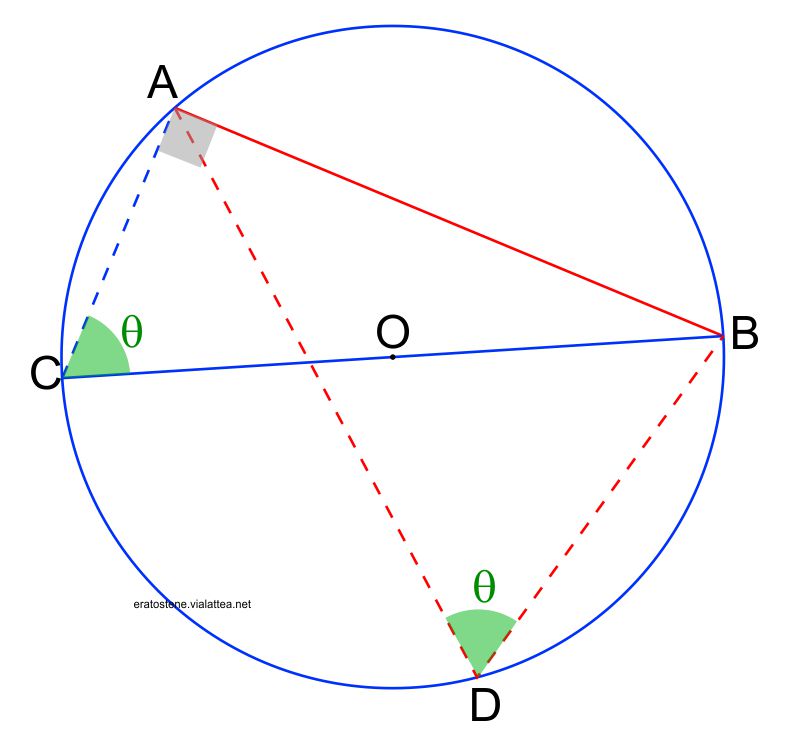
Il teorema della corda afferma che la lunghezza di una corda $AB$ è uguale alla lunghezza del diametro $2r$ per il seno dell’angolo alla circonferenza che insiste sulla quella corda:
$$\boxed{AB=2r\cdot\sin\theta}$$
Lo si dimostra costruendo un triangolo rettangolo $CAB$ inscritto nella stessa circonferenza che abbia la corda $AB$ come uno dei suoi cateti. Un qualsiasi triangolo rettangolo inscritto in una circonferenza si dispone necessariamente in un certo modo: la sua ipotenusa $CB$ coincide con il diametro. Ne consegue che:
$$AB=CB\cdot\sin\theta$$
e, dato che $CB=2r$:
$$AB=2r\cdot\sin\theta$$
come volevamo dimostrare.
Per mezzo del teorema della corda, si dimostra facilmente il teorema dei seni.
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

