La proiezione stereografica è una funzione che proietta la superficie di una sfera su un piano in cui il punto di proiezione è un punto stesso della sfera. Tutti i punti della sfera hanno una loro immagine nel piano di proiezione, a parte uno: il punto di proiezione stesso. Tutte le circonferenze sulla sfera si proiettano come circonferenze sul piano e questo è un primo grande vantaggio che permette di disegnare la proiezione usando soltanto la riga e il compasso ed evitando la necessità di costruire curve più complesse come ad esempio le ellissi che richiedono un tracciamento “punto per punto”. Il secondo grande vantaggio è la conservazione degli angoli che fornisce strategie semplici per risolvere alcuni problemi di proiezione apparentemente complessi come si incontrano ad esempio nella costruzione dell’astrolabio e nelle operazioni di localizzazione nautica. Attualmente questa proiezione è impiegata nei software astronomici per la visualizzazione grafica del cielo (vedi ad esempio Stellarium).

Ci sono molte versioni di proiezioni stereografiche ma qui esamineremo, come primo esempio, la versione tradizionalmente utilizzata per la costruzione degli astrolabi.
Si sceglie come punto di proiezione il polo sud celeste $P_S$. Il piano di proiezione è quello dell’equatore celeste. L’equatore celeste coincide con la sua proiezione e il centro, il punto $P$, corrisponde al centro della sfera celeste. Ad esso si sovrappone la proiezione del polo nord celeste.
Seguiamo le fasi della proiezione di un punto qualsiasi della sfera, come ad esempio la stella $S$. La retta che congiunge $P_S$ con la stella $S$ interseca il piano di proiezione nel punto $S’$. L’arco $P_N\,S\,P_S$ è l’orario della stella $S$. Esso si proietta nel piano come una semiretta che origine in $P$ e passa per $S’$. Analogamente, la stella $T$ appartenente allo stesso orario di $S$, si proietta nel punto $T’$.
Tutti i circoli orari sono rappresentati come semirette con l’origine comune in $P$.
Si può notare qui uno dei grandi vantaggi della proiezione stereografica rispetto alla proiezione ortografica: tutte le stelle, di entambi gli emisferi, si possono rappresentare teoricamente sul piano senza sovrapposizioni. Nella proiezione ortografica invece è necessario scegliere un solo emisfero da rappresentare. L’unica difficoltà pratica di cui tener conto consiste nella distanza della stella proiettata rispetto al centro $P$: più la stella è vicina al polo sud celeste $P_S$, più la sua proiezione sarà lontana da $P$. Per disegnare tutte le stelle sarebbe necessario un foglio di dimensioni infinite. L’unico punto teoricamente non proiettabile è il polo sud celeste, ma una scelta deve essere comunque fatta per mettere in evidenza l’emisfero di cielo che ci interessa rappresentare. In questo caso, con la scelta del punto di proiezione nel polo sud celeste, l’area è quella dell’emisfero nord, centrata nel polo nord celeste. Per rappresentare una buona parte di stelle anticircumpolari ci vorrebbe un foglio troppo grande.
In modo molto simile alla proiezione ortografica, anche qui i cerchi paralleli all’equatore (i paralleli di declinazione) si rappresentano come cerchi concentrici a $P$. Il secondo grande vantaggio, e forse il principale, rispetto alla proiezione ortografica, l’abbiamo già accennato all’inizio: ogni cerc hio, massimo o minore che siano, parallelo o non parallelo al piano di proiezione, conserva la forma di cerchio anche se il suo raggio subisce delle modifiche. La proiezione di un cerchio massimo avrà il raggio maggiore del raggio dell’equatore e sarà tanto più grande quanto maggiore sarà la sua inclinazione rispetto all’equatore.
Osserviamo in questo esempio l’orizzonte: il centro della sua proiezione si può trovare anche graficamente, segnando le proiezioni $C’$ e $D’$ di due suoi punti diametrali ($C$ e $D$). Il punto medio $O$ del segmento $C’D’$ è il centro dove puntare il compasso per disegnare la proiezione dell’orizzonte. Il raggio è uguale a $C’O$.
Notiamo qui che è immediata anche la comprensione delle posizioni delle stelle rispetto all’equatore e all’orizzonte: la stella $S’$ è all’interno del circolo dell’orizzonte e quindi la sua altezza è positiva. Inoltre essa è interna anche al circolo dell’equatore e perciò anche la sua declinazione è positiva. Al contrario, la stella proiettata in $T’$ si trova nell’emisfero celeste sud e nell’emisfero invisibile, al di sotto dell’orizzonte, perché è esterna a entrambi i cerchi.
Proiezione di un punto
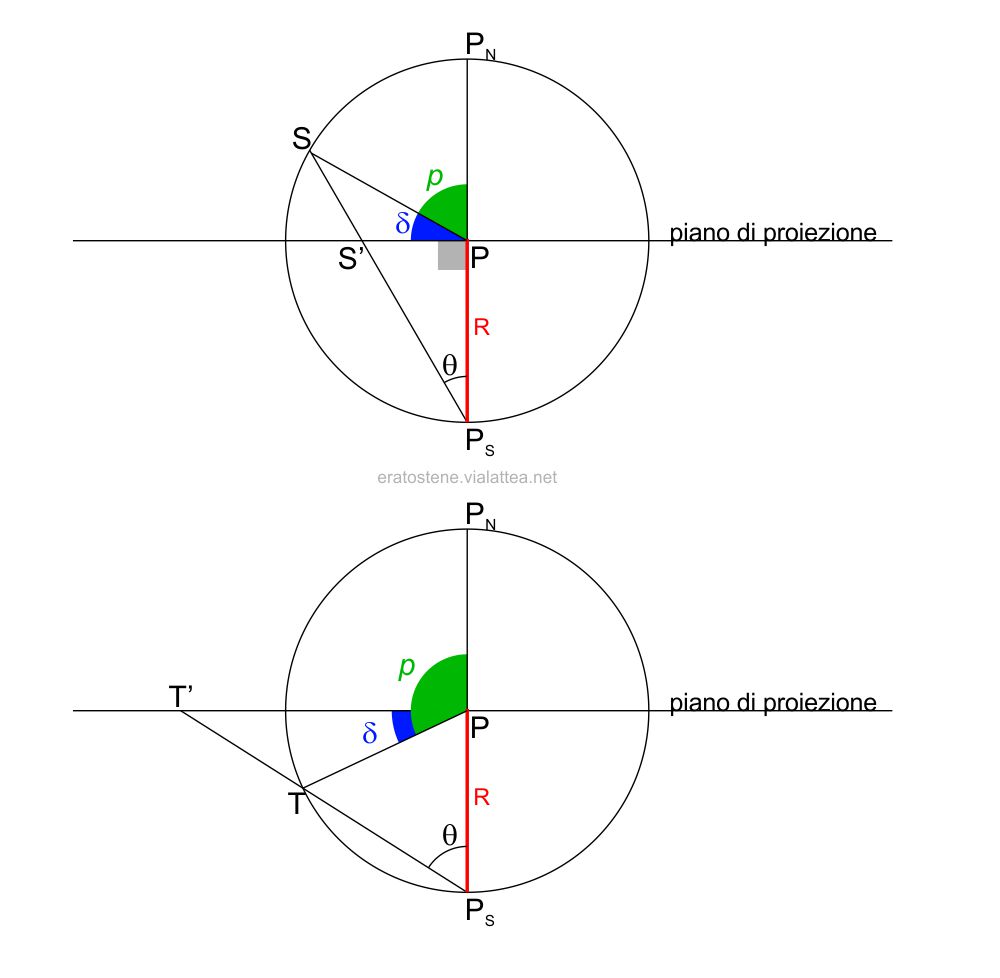
Un punto $S$ sulla sfera celeste, di declinazione $\delta$, ha la sua proiezione in $S’$ sul piano di proiezione.
La distanza $PS’$ può essere calcolata facilmente in funzione del raggio della sfera $R$ e della declinazione $\delta$, oppure della distanza polare $p=90^1circ-\delta$.
Si noti infatti il triangolo rettangolo $S’PP_s$ retto in $P$ di cui è noto il cateto $PP_S=R$. L’angolo $\theta$ è la metà della distanza polare $p$ perché $p$ è l’angolo al centro che sottende l’arco $P_N S$ e l’angolo $\theta$ è il corrispondente angolo alla circonferenza. Perciò:
$$\theta = \frac{p}{2} = \frac{90^\circ-\delta}{2}$$
A questo punto il triangolo $S’PP_s$ può essere risolto per via trigonometrica. Il segmento che ci interessa è il cateto $PS’$:
$$\boxed{PS’ = R\tan\theta= R\tan\frac{p}{2} = R\tan\frac{90^\circ-\delta}{2}}$$
La funzione produce il risultato corretto anche nel caso di una stella $T$ appartenente all’emisfero sud con $\delta<0$.
Proiezione di una circonferenza

Immaginiamo ora di dover disegnare la proiezione di un cerchio massimo, come ad esempio l’eclittica $AB$ inclinata dell’angolo $\epsilon$ rispetto all’equatore celeste (quest’ultimo coincide con il piano di proiezione). La costruzione grafica è semplice ed è rappresentata nella figura a fianco. Si disegna innanzitutto il diametro $AB$ inclinato di $\epsilon$ gradi rispetto al piano. Si trovano le proiezioni $A’$ e $B’$ come si è fatto nell’esempio precedente per la proiezione dei punti. Quindi si trova il punto medio $O$ del segmento $A’B’$, centro della circonferenza proiettata. Il raggio è $r=OA’$ e il punto $O$ dove puntare il compasso si trova alla distanza $d=OP$ dal centro $P$ dell’equatore.
Le posizioni di $A’$ e di $B’$ rispetto a $P$ si calcolano in questo modo:
$$PB’=R\tan\frac{90^\circ-\epsilon}{2}$$
$$PA’=R\tan\frac{90^\circ+\epsilon}{2}$$
Il raggio $r=OA’$ si trova:
$$r=\frac{PB’+PA’}{2}$$
La distanza $d=OP$ si trova:
$$d =r-PB’$$
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

