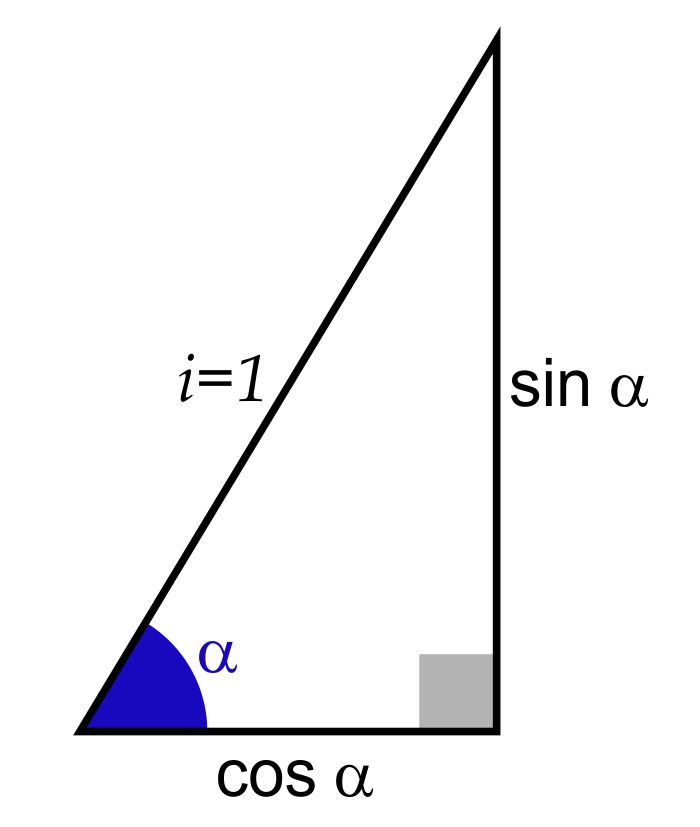
L’identità fondamentale mette in relazione il seno e il coseno e ci permette di ricavare l’uno conoscendo l’altro. Deriva essenzialmente dalla definizione delle funzioni trigonometriche e dal teorema di Pitagora:
$$\boxed{\sin^2\alpha+\cos^2\alpha=1}$$
$$\sin\alpha=\pm\sqrt{1-\cos^2\alpha}$$
$$\cos\alpha=\pm\sqrt{1-\sin^2\alpha}$$
(Il segno da attribuire alle ultime due uguaglianze non è arbitrario: il seno è positivo se si trova nel primo o nel secondo quadrante e il coseno è positivo se si trova nel primo o nel quarto quadrante. In tutti gli altri casi il segno è negativo).
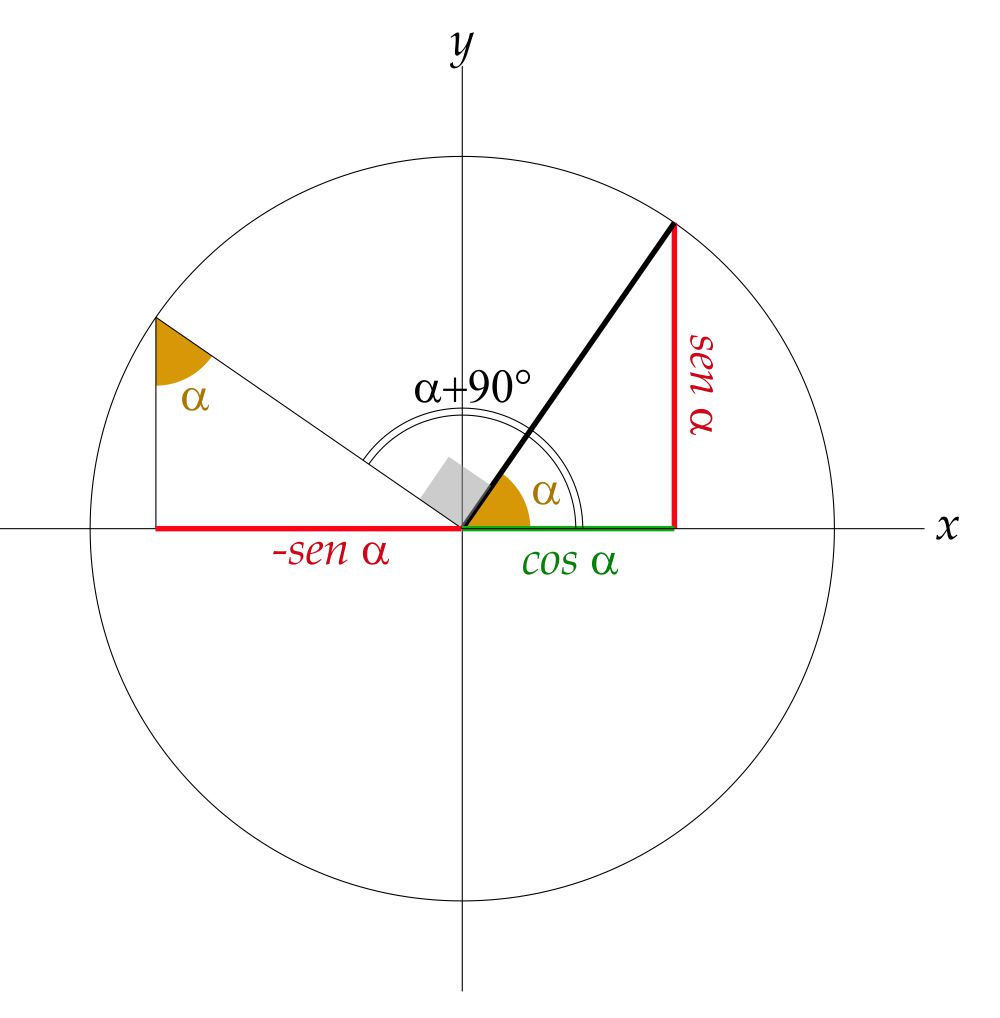
Le seguenti uguaglianze si possono facilmente verificare per via grafica, aggiungendo o togliendo angoli retti all’angolo $\alpha$ disegnato nel cerchio trigonometrico. Altre formule analoghe a queste si ottengono aggiungendo o togliendo angoli piatti. Ad esempio, lo schema qui a fianco aiuta a dimostrare la seconda uguaglianza di questo elenco; si basa sulla congruenza dei due triangoli rettangoli disegnati nel cerchio trigonometrico.
$$\sin{(\alpha\pm90^\circ)}=\pm\cos{\alpha}$$
$$\cos{(\alpha\pm90^\circ)}=\mp\sin{\alpha}$$
$$\tan{(\alpha\pm90^\circ)}=-\cot{\alpha}$$
$$\cot{(\alpha\pm90^\circ)}=-\tan{\alpha}$$
$$\cos(180^\circ\pm\alpha)=-\cos\alpha$$
$$\sin(180^\circ\pm\alpha)=\mp\sin\alpha$$
$$\tan(180^\circ\pm\alpha)=\pm\tan\alpha$$
$$\cot(180^\circ\pm\alpha)=\pm\cot\alpha$$

Le funzioni trigonometriche di angoli complementari si intuiscono e dimostrano facilmente costruendo degli schemi grafici analoghi a quello rappresentato qui a fianco riguardante il seno e il coseno.
$$\cos(90^\circ-\alpha)=\sin\alpha$$
$$\sin(90^\circ-\alpha)=\cos\alpha$$
$$\tan(90^\circ-\alpha)=\cot\alpha$$
$$\cot(90^\circ-\alpha)=\tan\alpha$$
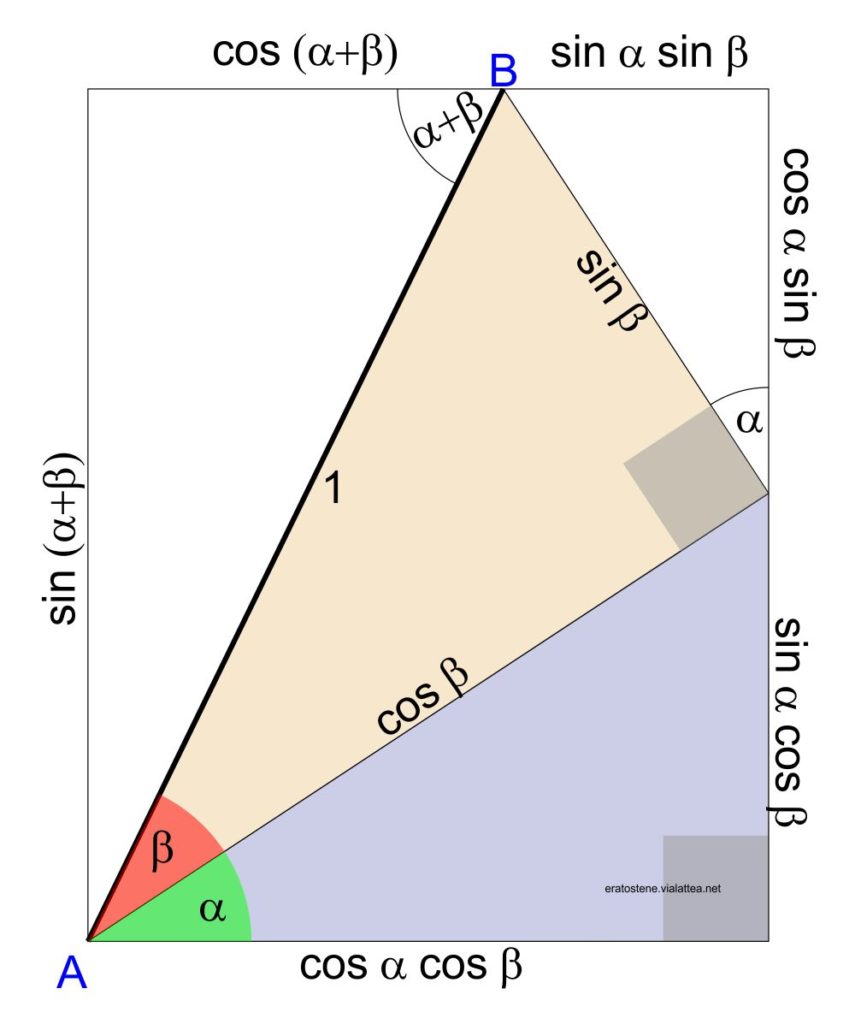
Da questo schema grafico, costruito sulla condizione che il segmento $AB$ sia il raggio unitario del cerchio trigonometrico, si possono dimostrare facilmente le formule di addizione:
$$\sin{(\alpha+\beta)} = \cos\alpha\cdot\sin\beta+\sin\alpha\cdot\cos\beta$$
$$\cos{(\alpha+\beta)} =\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta$$

Apportando una variazione nella collocazione dell’angolo $\alpha$, si possono dimostrare con lo stesso sistema le formule di sottrazione:
$$\cos{(\alpha-\beta})=\sin\alpha\cdot\sin\beta+\cos\alpha\cdot\cos\beta$$
$$\sin{(\alpha-\beta)}=\sin\alpha\cdot\cos\beta-\cos\alpha\cdot\sin\beta$$
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

