Chi si diverte a realizzare i nostri piccoli esperimenti si imbatte spesso nella necessità di dover disegnare un angolo di una certa misura, con la massima precisione possibile. In questi casi il goniometro è decisamente lo strumento meno indicato: pur prestando molta attenzione si sbaglia facilmente di $\pm1^\circ$. La tecnica migliore è quella di usare un po’ di trigonometria costruendo sempre dei triangoli rettangoli.
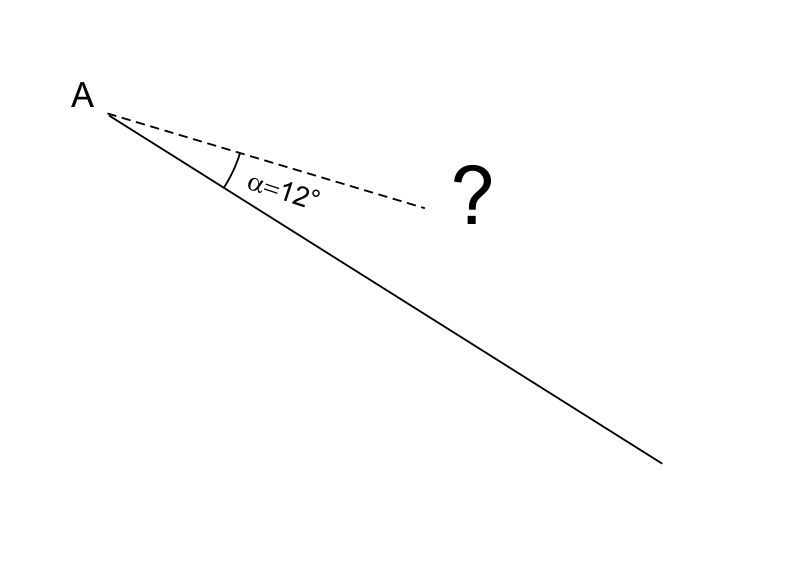
Ad esempio, come disegnare un angolo $\alpha$ di $12^\circ$ antiorario con vertice in $A$ senza usare il goniometro?

Ecco il metodo:
- prolungare il lato il più possibile fino ad un punto $B$. La lunghezza massima dipende dalle dimensioni del foglio e dall’ampiezza dell’angolo da disegnare
- Tracciare una retta perpendicolare ad $AB$ che passi per $B$
- Misurare la lunghezza del lato $\overline{AB}$
- Fissare un punto $C$ sulla perpendicolare in modo che la distanza $\overline{BC}$ risulti dal seguente calcolo:
$\overline{BC}=\overline{AB}\cdot\tan\alpha$ - Tracciare il lato $AC$ per ottenere l’angolo desiderato.
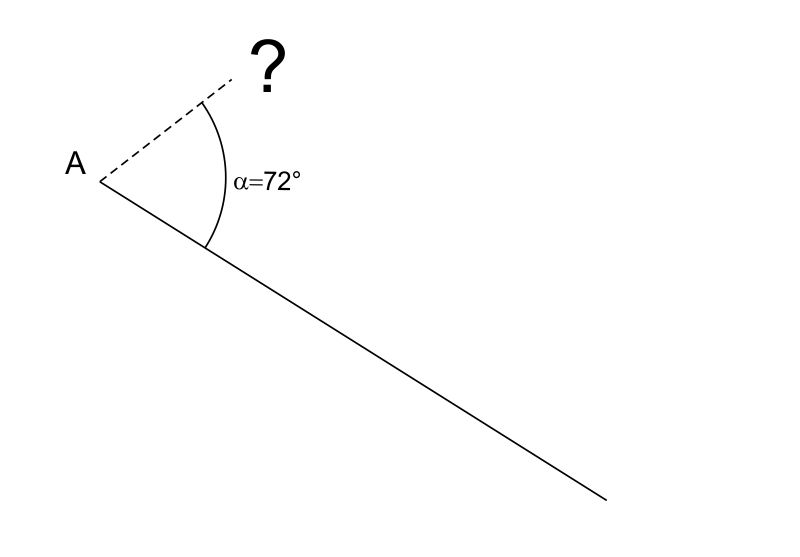
L’operazione funziona bene per angoli acuti inferiori ai $45^\circ$. Se l’ampiezza dell’angolo è maggiore di $45^\circ$ conviene lavorare con il suo complementare.

- calcolare $\beta=90^\circ-\alpha$
- tracciare la perpendicolare al lato che passa per il vertice $A$ e che raggiunga un punto $B$ più lontano possibile.
- tracciare la perpendicolare ad $AB$ che passa per $B$
- misurare la lunghezza di $\overline{AB}$
- segnare su quest’ultima un punto $C$ in modo tale che la lunghezza di $\overline{BC}$ sia quella ottenuta dal seguente calcolo:
$\overline{BC}=\overline{AB}\cdot\tan\beta$ - tracciare il lato $AC$ per ottenere l’angolo desiderato.
Nel caso di angoli maggiori di $90^\circ$ si usano vari “trucchi” che si scoprono con la pratica, togliendo dall’angolo parti di $90^\circ$ o di $180^\circ$, oppure prolungando il lato oltre il vertice, in modo da lavorare sempre con angoli acuti.
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

