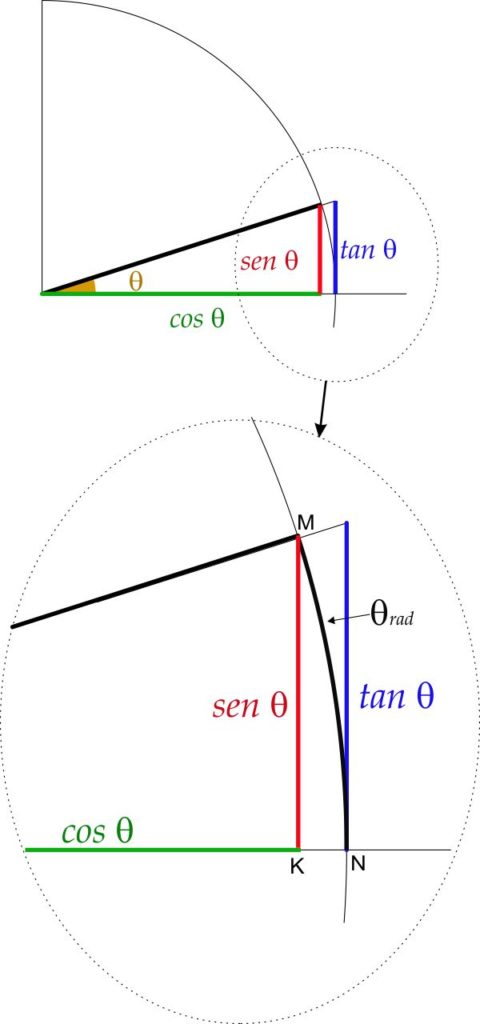
Se un angolo $\theta$ è abbastanza piccolo, si ricorre spesso ad un’approssimazione utile sia per semplificare i calcoli che per semplificare le equazioni.
Si nota facilmente che l’arco di cerchio $\overset{\frown}{MN}$ ha una lunghezza intermedia tra il valore di $\sin \theta$ e il valore di $\tan \theta$ e che la differenza tra queste tre lunghezze diventa sempre più piccola diminuendo l’ampiezza di $\theta$.
D’altra parte, nel cerchio a raggio unitario, la lunghezza dell’arco $\overset{\frown}{MN}$ è uguale al valore dell’ampiezza dell’angolo $\theta$ espresso in radianti.
Perciò, quando lo si ritiene utile, si può scrivere:
$$\sin\theta \simeq \tan\theta \simeq \theta$$
La differenza $\overline{KN}$ tra il valore del coseno di $\theta$ e il valore $1$ del raggio unitario invece è un po’ più grande della precedente differenza. Il coseno è approssimabile con la seguente funzione:
$$cos \theta \simeq 1-\frac{\theta^2}{2}$$
sempre se il valore di $\theta$ è espresso in radianti.
Nella pratica, talvolta è utile esprimere l’angolo $\theta$ in gradi, primi, ma più spesso in arcosecondi. Sapendo che :
$$1^{rad}=\text{57,3}^\circ=3438’=206\,265”$$
basterà moltiplicare l’angolo $\theta$ per il fattore di conversione desiderato.
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

