La proiezione ortografica permette di raffigurare un emisfero della sfera celeste (normalmente l’emisfero celeste nord o sud, oppure l’emisfero visibile) su un piano. I segmenti che congiungono i punti della sfera con le loro proiezioni sul piano sono tutti paralleli tra loro e perpendicolari al piano di proiezione. Detto in altre parole, il punto di proiezione è a distanza infinita.
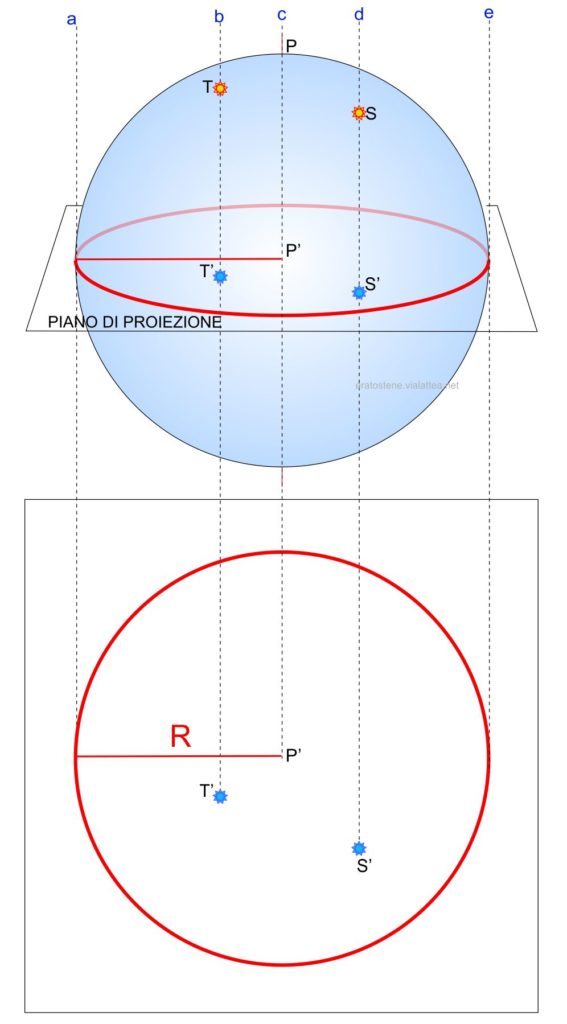
Le rette di proiezione ($a, b, c, d$ ed $e$) sono tutte parallele tra loro. Il bordo della sfera celeste si proietta nel piano di proiezione come un cerchio. La stella $S$ si proietta nel punto $S’$ e la stella $T$ nel punto $T’$. Il punto $P$ che è uno dei poli del cerchio massimo che giace sul piano di proiezione, si proietta nel centro $P’$ che è il centro del cerchio di raggio $R$ uguale al raggio della sfera.
Normalmente si sceglie come piano di proiezione l’equatore e come punto di proiezione il polo celeste nord o sud. In questo modo si ottiene la proiezione dell’emisfero nord o sud. Un’altra tipica proiezione ortografica della sfera celeste è quella sul piano dell’orizzonte. In questo caso il punto di proiezione coincide con lo zenit.
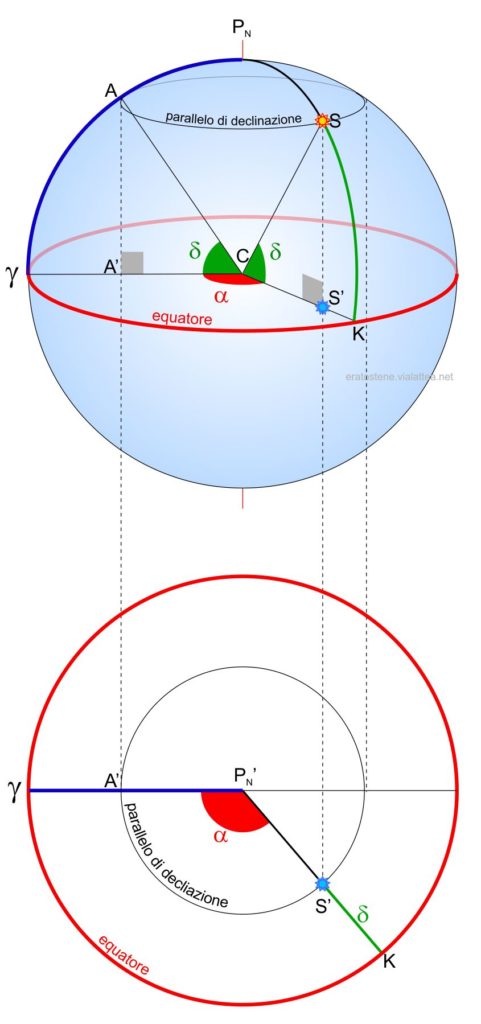
Come esempio, si raffigura qui una proiezione sul piano equatoriale dell’emisfero celeste nord. Il polo celeste nord $P_N$ si proietta nel centro del cerchio di proiezione, che coincide anche con il centro $C$ della sfera celeste. I semicircoli orari si proiettano sul piano come dei raggi. Ad esempio, il semicerchio orario della stella $S$ si proietta come il segmento $P_N’K$. Il punto $\gamma$ è il punto vernale. Il suo semicerchio circolo orario $P_N A \gamma$ si proietta sul piano nel segmento $P_N’\gamma$.
I paralleli di declinazione, che sono cerchi minori paralleli al piano equatoriale, si proiettano sul piano come cerchi concentrici e il loro raggio dipende dalla declinazione dei loro punti.
Si calcola facilmente il raggio di un parallelo di declinazione considerando il triangolo $CAA’$, retto in $A’$. L’angolo in $C$ è la sua declinazione $\delta$. Se $R=CA$ è il raggio della sfera, il segmento $CA’=P_N’A’$ si calcola con l’espressione:
$$CA’=R\cos\delta$$
E’ molto semplice disegnare il punto $S’$ che è la proiezione della stella $S$ appartenente allo stesso parallelo di declinazione e la cui ascensione retta è $\alpha$. La sua distanza dal centro $P_N’S’$ si calcola con la formula precedente in base al valore di $\delta$ e la sua ascensione retta decide l’angolo da misurare rispetto alla direzione del punto vernale $\gamma$, contato in senso antiorario.
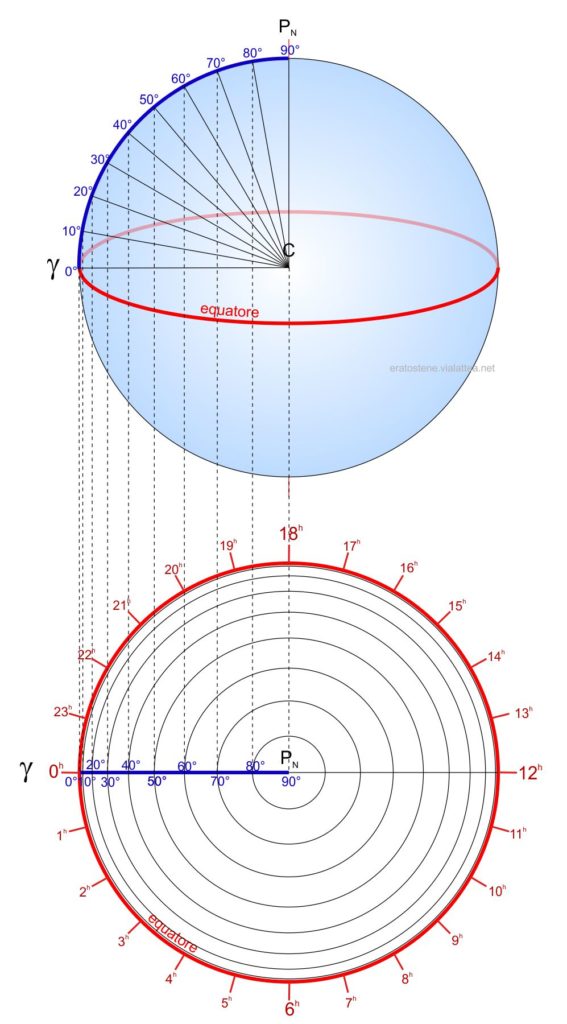
Le due coordinate equatoriali, ascensione retta $\alpha$ e declinazione $\delta$, sono perciò facilmente riproducibili. Le coordinate orarie sono quasi identiche: cambia solo la rappresentazione dell’angolo orario che, a differenza dell’ascensione retta, ha come origine il mezzocielo superiore al posto del punto vernale e si conta in senso orario. Il diagramma orario è un’utile applicazione della proiezione ortografica equatoriale che permette di visualizzare le relazioni tra ascensione retta, tempi e longitudine (vedi ad esempio Il tempo e l’ascensione retta e Il tempo e le differenze di longitudine).
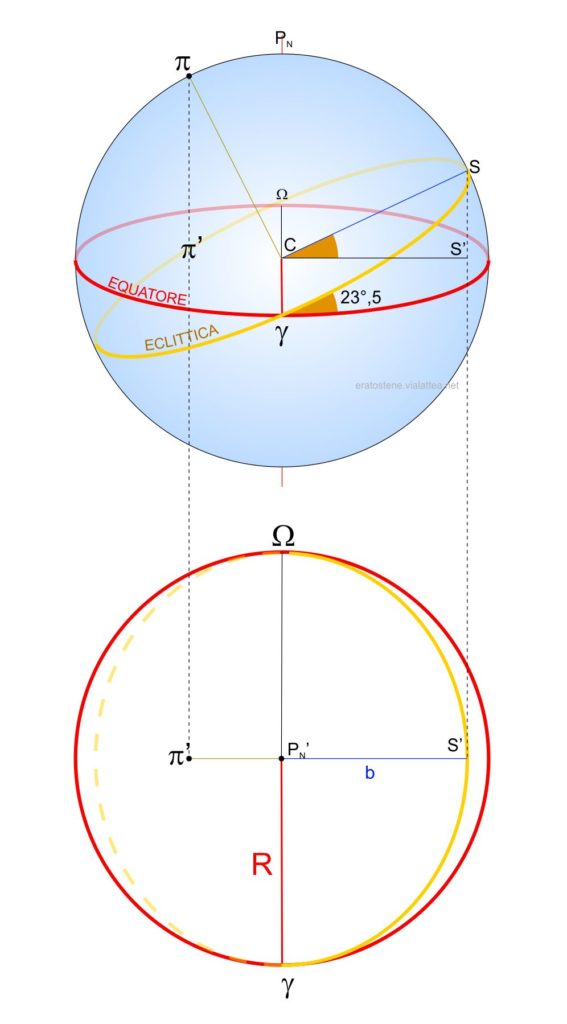
Nelle proiezioni ortografiche, tutti i cerchi non paralleli al piano di proiezione assumono l’aspetto di ellissi. In questo esempio si rappresenta l’eclittica inclinata di $23.4^\circ$ rispetto all’equatore. Nell’emisfero nord compare solo l’arco di eclittica con declinazione positiva. L’ellisse dell’eclittica ha come semiasse maggiore il raggio $R$ della sfera e come semiasse minore il segmento $P_N’S’=b$ che si calcola:
$$b=R\cos{23.4^\circ}$$
I nodi dell’eclittica sono il punto vernale $\gamma$ e il primo punto della Bilancia $\Omega$. Il punto $S’$ rappresenta il punto dell’eclittica con declinazione massima, cioè il punto solstiziale di giugno.
Allo stesso modo si può rappresentare l’orizzonte: esso si proietterà come un’ellisse che ha per semiasse maggiore sempre $R$ e come semiasse minore $R\cos(90^\circ-\varphi)$ dove $\varphi$ è la latitudine dell’osservatore.
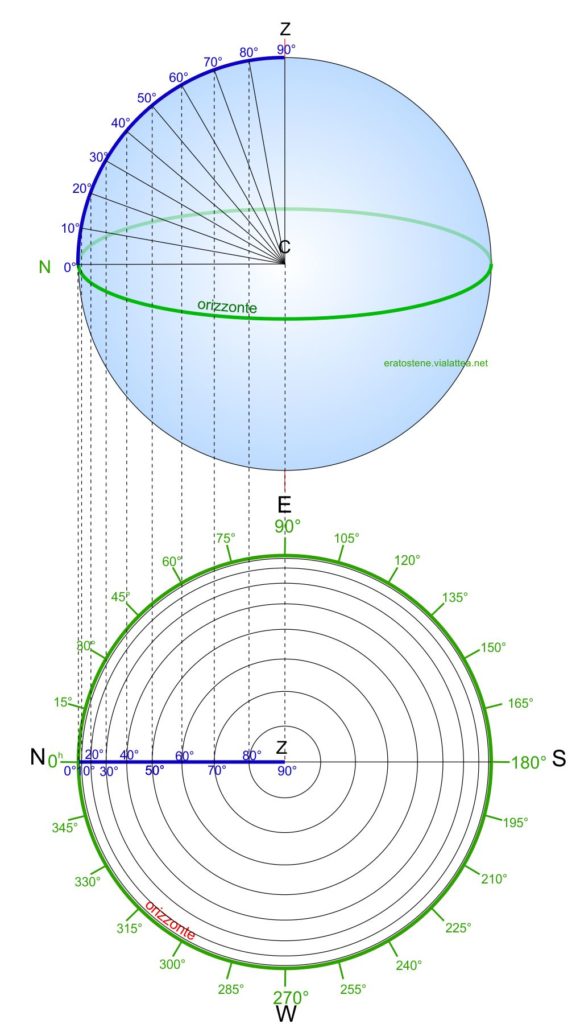
Molto simile alla proiezione ortografica equatoriale è la proiezione ortografica orizzontale che proietta sul piano dell’orizzonte astronomico. Il punto di proiezione, al centro del grafico, in questo caso sarà lo zenit $Z$; gli almucantarat saranno proiettati come dei centri concentrici i cui raggi sono funzione della loro altezza; la scala dell’azimut parte dal punto cardinale nord $N$ ed è contata in senso orario.
L’equatore e l’eclittica si proietteranno sul piano dell’orizzonte in forma di ellissi.
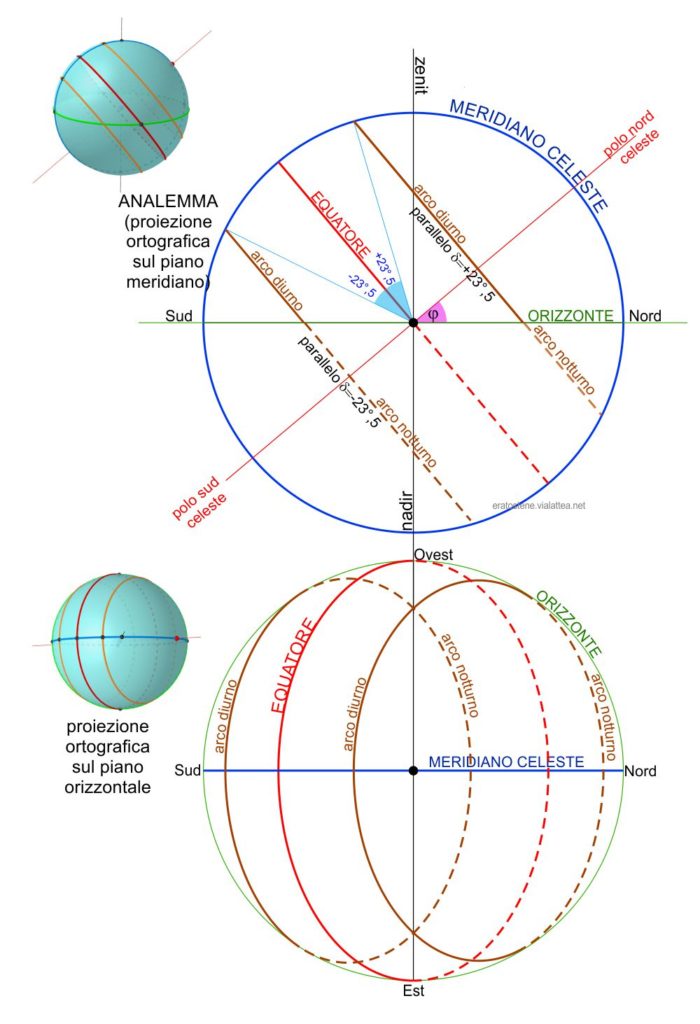
Ultimo ma non meno interessante tipo di proiezione ortografica è l’analemma: una proiezione sul piano meridiano. Per una descrizione dettagliata vedi L’analemma di Vitruvio.
- Angoli
- Le principali funzioni trigonometriche
- Risolvere un triangolo rettangolo
- Trigonometria utile
- Risolvere un triangolo qualsiasi
- Il teorema della corda
- Approssimazione per angoli piccoli
- Triangolo sferico
- Il triangolo sferico rettangolo e rettilatero
- L’ellisse
- Disegnare un angolo con la calcolatrice
- Proiezione ortografica
- Proiezione stereografica
- Coordinate nel piano e nello spazio

