La longitudine di un luogo è in semplice e stretta relazione con la misura del tempo. Il tempo di un astro è un angolo e sono angoli pure le differenze di longitudine tra due luoghi di osservazione. Prima ancora di affrontare le questioni del meridiano di riferimento per le longitudini, esaminiamo un concetto generale.
Consideriamo due osservatori, $A$ e $B$ che si trovano in due diverse località della Terra. Le loro longitudini sono diverse, rispettivamente $\lambda_A$ e $\lambda_B$. Ognuno degli osservatori ha il proprio meridiano celeste.
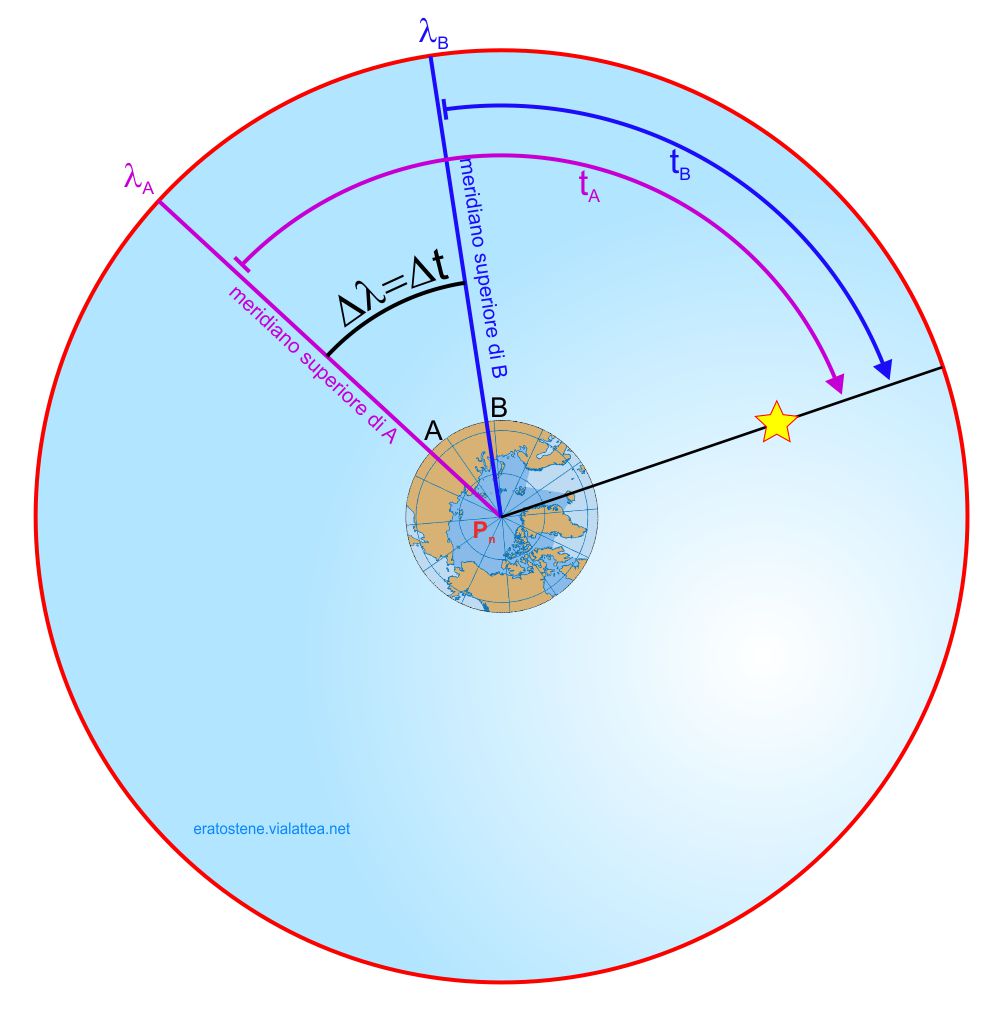
Essi misurano simultaneamente l’angolo orario di uno stesso astro. L’osservatore $A$ misura l’angolo orario $t_A$ e l’osservatore $B$ misura l’angolo orario $t_B$.
Lo schema qui a fianco è un diagramma orario:, cioè una proiezione della sfera celeste sul piano dell’equatore. Il polo nord celeste è al centro (dove si trova la Terra) e il circolo di contorno è l’equatore celeste.
La longitudine dell’osservatore $A$ è, per convenzione, maggiore della longitudine dell’osservartore $B$ perché il primo si trova ad est del secondo. Risulta evidente che la differenza tra i due angoli orari misurati simultanei è uguale alla differenza di longitudine dei due osservatori:
$$\boxed{t_A-t_B=\lambda_A-\lambda_B}$$
Due osservatori possono così misurare la loro differenza di longitudine accordandosi e misurando simultaneamente l’angolo orario di una stessa stella, visibile a entrambi.
E’ importante notare qui che il sistema funziona solo se l’astro osservato è abbastanza lontano dalla Terra da non presentare un angolo di parallasse rilevabile tra i due osservatori. Il Sole o una stella, ad esempio, sono oggetti adatti allo scopo mentre la Luna porterebbe a notevoli errori di misurazione di longitudine.
Questa relazione fondamentale tra angolo orario e longitudine ha numerose e interessanti conseguenza. Aiutandoci con le immagini, ne vedremo alcuni risvolti.
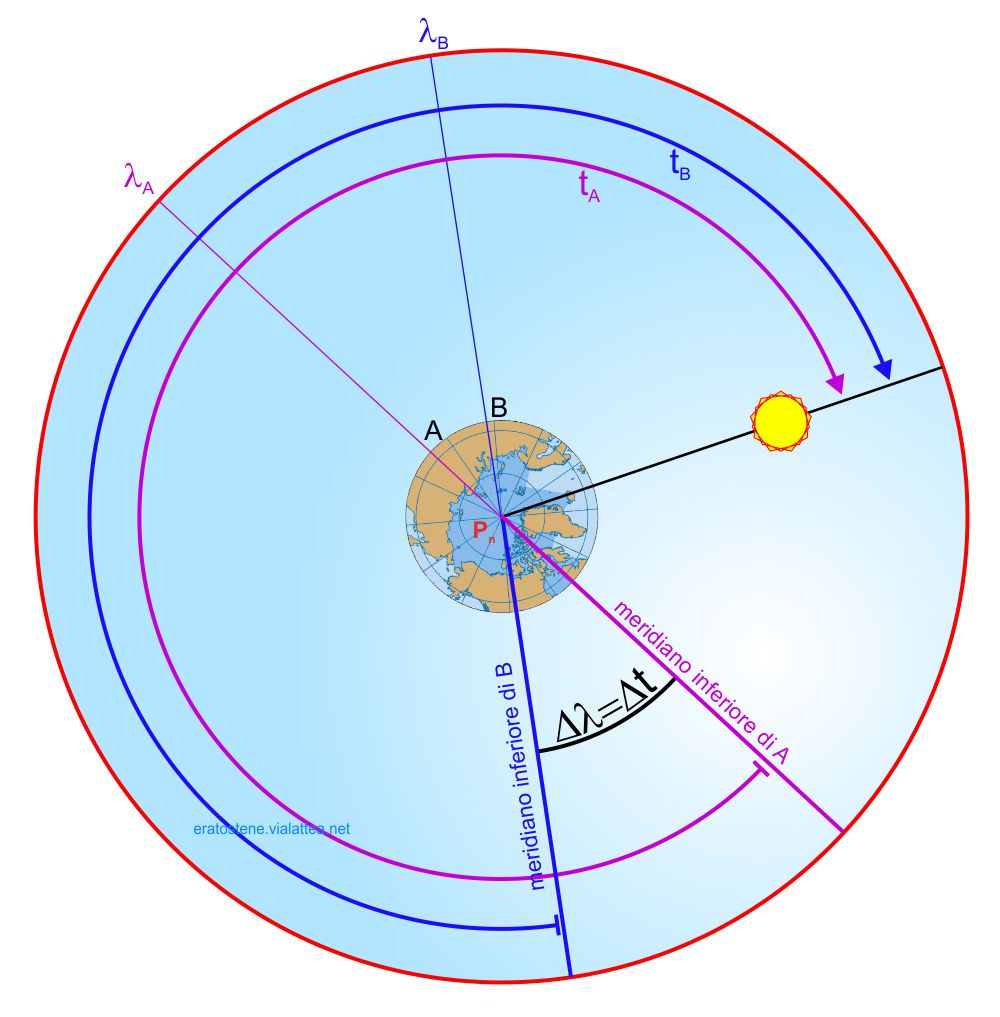
La differenza di longitudine è legata in modo analogo anche ai tempi solari simultanei di due luoghi, pur essendo misurati nella variante di tempi solari civili, cioè misurando l’angolo del Sole rispetto al meridiano inferiore. La relazione si applica ugualmente ai tempi solari veri come pure ai tempi solari medi.
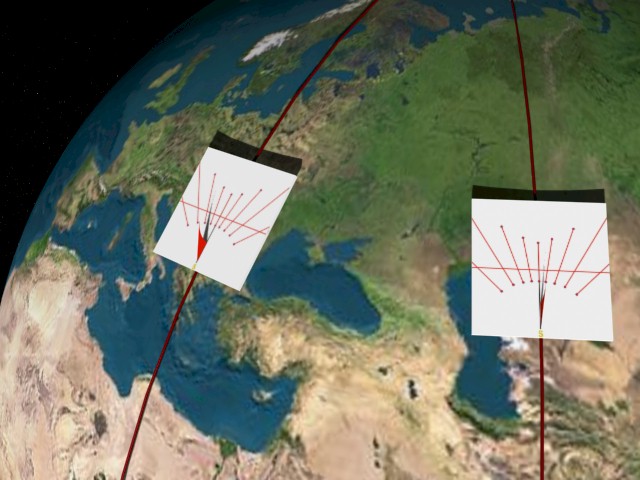
Ne consegue, ad esempio, che due osservatori posti in due luoghi diversi possono misurare la differenza di longitudine semplicemente eseguendo una lettura simultanea dei loro orologi solari. La differenza di ora solare vera è uguale alla differenza tra le longitudini delle due località.
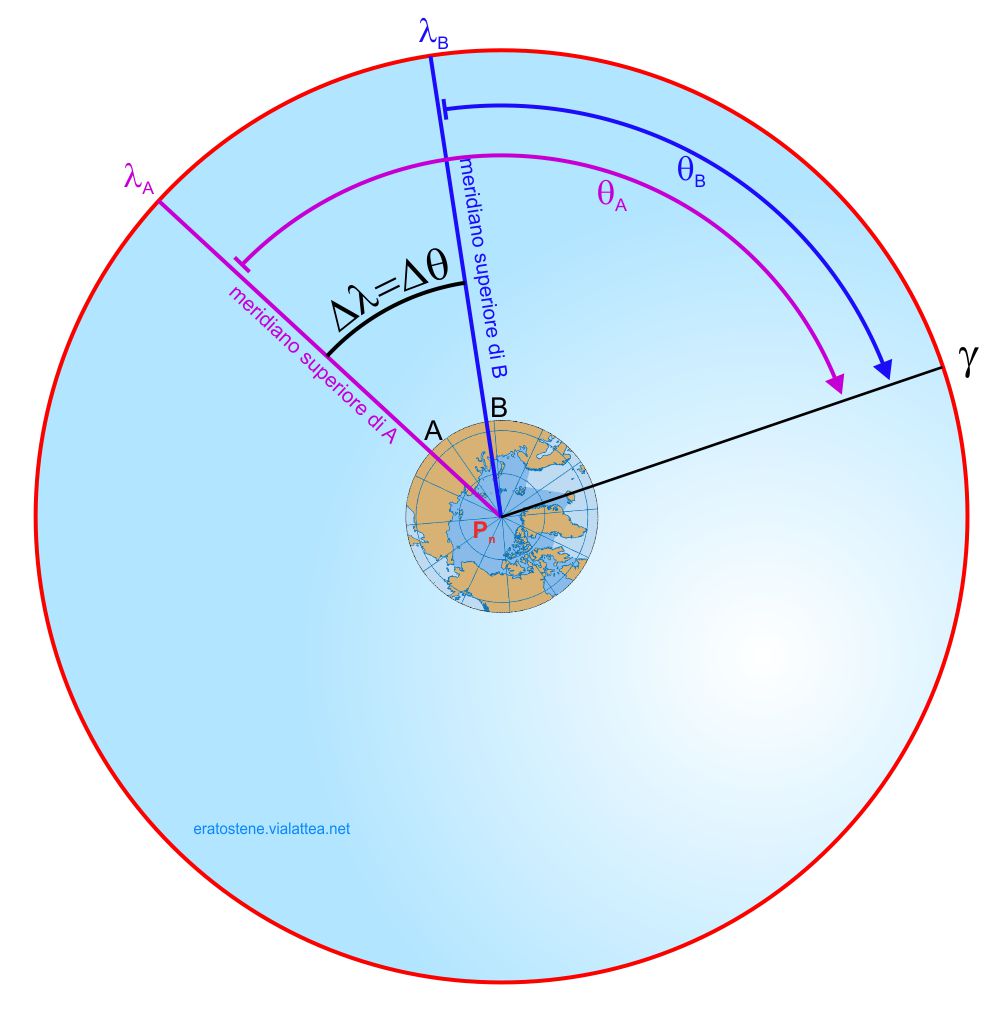
Il tempo siderale, in quanto angolo orario del punto vernale $\gamma$, è soggetto alla stessa semplice relazione. Possiamo dire perciò che la differenza dei tempi siderali locali simultanei di due osservatori è uguale alla loro differenza di longitudine.
- La misura del tempo: una introduzione
- Il diagramma orario
- Giorni e tempi
- Il giorno siderale e il tempo siderale
- Giorno siderale e giorno solare
- Il giorno solare non è un intervallo costante
- L’anno tropico e l’anno siderale
- L’introduzione del giorno solare medio: un intervallo di tempo costante
- L’equazione del tempo
- Giorno astronomico e giorno civile
- Il tempo e le differenze di longitudine
- Il tempo e l’ascensione retta
- Tempi locali e tempi del meridiano fondamentale
- Tempo meccanico e tempo dell’orologio solare
- Tempo medio, tempo siderale e conversioni
- L’irregolarità della rotazione terrestre e i tempi atomici
- Sole medio e Sole vero

