La suddivisione della superficie terrestre in 24 fusi orari di $15^\circ$ ciascuno è una comoda convenzione per regolare il tempo civile. Qui è interessante notare come sia possibile determinare in modo veloce e pratico il tempo medio locale in base alla longitudine del luogo e al fuso orario di appartenenza. E’ un operazione che può essere utile a chi si diletta di orologi solari. E’ importante innanzitutto capirsi sui termini.
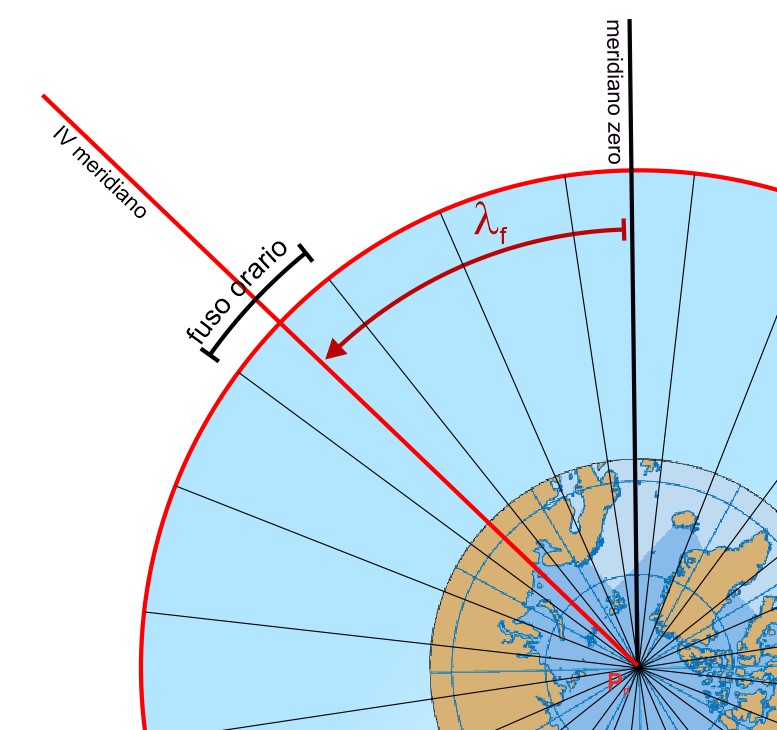
Qui ha fianco è rappresentata schematicamente una parte della suddivisione in fusi orari. Il quarto meridiano si trova a est del meridiano zero e dista $4\times15^\circ=60^\circ$ di longitudine da esso. Si vede dalla figura che ogni fuso orario è bisecato dal proprio meridiano che per questo motivo è chiamato meridiano centrale del fuso. Quello rappresentato in figura è il meridiano centrale del quarto fuso orario. Il meridiano centrale dista $\text{7,5}^\circ$ di longitudine ciascuno dei due bordi del fuso.
La longitudine del quarto meridiano centrale è $\lambda_f=60^\circ=4^h$. Tutti i meridiani centrali distano un’ora di longitudine tra loro.
Come si è visto nella pagina riguardante Il tempo e le differenze di longitudine, la differenza di longitudine tra il meridiano di un qualsiasi luogo e il meridiano zero corrisponde anche ad una differenza di tempo solare medio simultaneo misurato ai due meridiani.
La longitudine $\lambda_f$ corrisponde alla differenza di $4^h$ tra il tempo solare medio misurato al quarto meridiano centrale e il tempo solare medio misurato al meridiano zero.
Gli abitanti delle località che si trova all’interno del quarto fuso orario regolano l’orologio sul tempo medio del meridiano centrale del fuso. Però il tempo medio locale di un qualsiasi punto all’interno del fuso non coincide con il tempo medio del fuso a meno che il punto non si trovi esattamente sul meridiano centrale.
Per determinare agevolmente il tempo medio locale di un luogo di osservazione, si applica una correzione al tempo medio del fuso chiamata correzione del fuso o costante locale $C$ che equivale alla differenza espressa in ore tra la longitudine $\lambda$ dell’osservatore e la longitudine $\lambda_f$ del meridiano centrale del fuso.
$$\boxed{C=\lambda-\lambda_f}$$
Ad esempio, se il luogo si trova $6^\circ$ ad est del meridiano centrale del quarto fuso, la costante locale è $+6^\circ = 6\times\left(\frac{1}{15}\right)^h=+0,4^h=+24^m$.
Il tempo medio locale $t_L$ sarà perciò uguale al simultaneo tempo medio al meridiano centrale del fuso $t_F$ sommato alla costante locale $C$:
$$\boxed{t_L=t_F+C}$$
Una seconda correzione con l’equazione del tempo $E_t$ ci permette infine di calcolare il tempo solare vero locale $t_V$, cioè il tempo che segnerà un orologio solare posizionato a quella longitudine.
Come abbiamo visto, l’equazione del tempo è la differenza tra il tempo vero e il tempo medio. Perciò:
$$\boxed{t_V = t_F + C + Et}$$
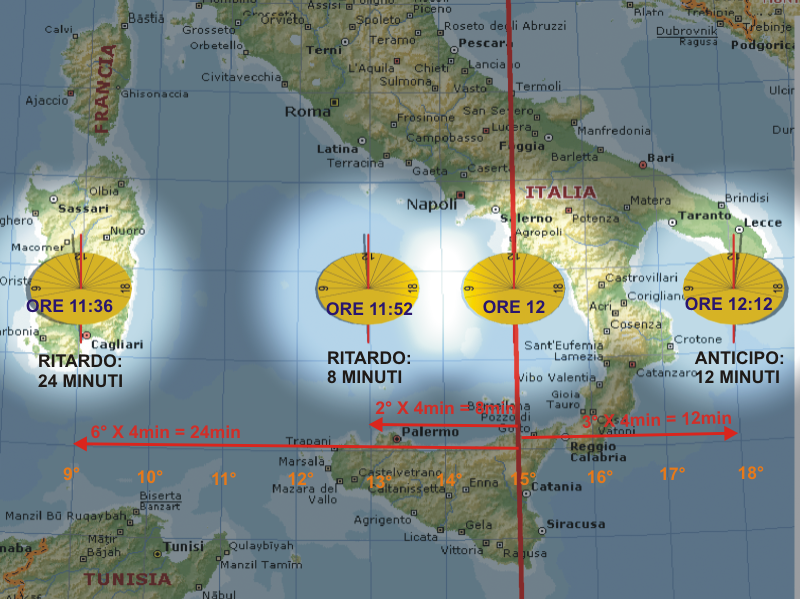
In questa immagine presenta alcuni esempi di ore solari vere locali misurate simultaneamente da alcuni orologi solari in base alla loro costante di longitudine (si trascura per semplicità la correzione dell’equazione del tempo).
Ad esempio, il primo orologio solare a sinistra ha una distanza in longitudine di $15^\circ-9^\circ=6^\circ$ a ovest dal meridiano centrale del fuso che passa per Catania. La costante di longitudine è perciò:
$C=-6^\circ = -24^m$
Se l’orologio solare posto sul meridiano centrale del fuso segna le ore $12$, questo segnerà simultaneamente le ore $12^h-24^m =11^h36^m$
In conclusione, la trasformazione del tempo segnato dai nostri orologi da polso nel tempo vero solare segnato da un orologio solare, e viceversa, comporta due correzioni: la correzione del fuso che è dovuta esclusivamente alla nostra posizione sulla Terra, in particolare alla nostra longitudine, e la correzione dell’equazione del tempo dovuta esclusivamente alla data.
- La misura del tempo: una introduzione
- Il diagramma orario
- Giorni e tempi
- Il giorno siderale e il tempo siderale
- Giorno siderale e giorno solare
- Il giorno solare non è un intervallo costante
- L’anno tropico e l’anno siderale
- L’introduzione del giorno solare medio: un intervallo di tempo costante
- L’equazione del tempo
- Giorno astronomico e giorno civile
- Il tempo e le differenze di longitudine
- Il tempo e l’ascensione retta
- Tempi locali e tempi del meridiano fondamentale
- Tempo meccanico e tempo dell’orologio solare
- Tempo medio, tempo siderale e conversioni
- L’irregolarità della rotazione terrestre e i tempi atomici
- Sole medio e Sole vero

