Riassumento ciò che si è detto nella pagina precedente, la differenza tra il tempo del Sole vero e il tempo del Sole medio è dovuta a due fattori:
- La Terra percorre un’orbita ellittica attorno al Sole. La Terra ha un moto non uniforme e il Sole non occupa il centro dell’ellisse ma uno dei fuochi; di conseguenza anche il moto apparente annuo del Sole lungo l’eclittica (che è la proiezione circolare del suo percorso sulla sfera celeste) non è uniforme.
- L’eclittica è inclinata di circa $\text{23,4}^\circ$ rispetto all’equatore celeste per cui, anche se il Sole avesse un moto apparente uniforme lungo l’eclittica, per percorrere tratti uguali di eclittica impiegherebbe comunque intervalli di tempo solare diversi (vedi Archi di eclittica e archi di equatore).
Il conteggio del tempo medio si discosta perciò da quello del tempo vero con una variazione ciclica annuale che accumula di giorno in giorno le differenze tra l’intervallo variabile del giorno vero e quello del giorno medio.
L’equazione del tempo ($E_t$), rappresenta questo “accumulo quotidiano di differenze” ed è definita come la differenza tra il tempo solare vero ($t_v$) e il simultaneo tempo solare medio ($t_m$), entrambi misurati a partire dal meridiano superiore.
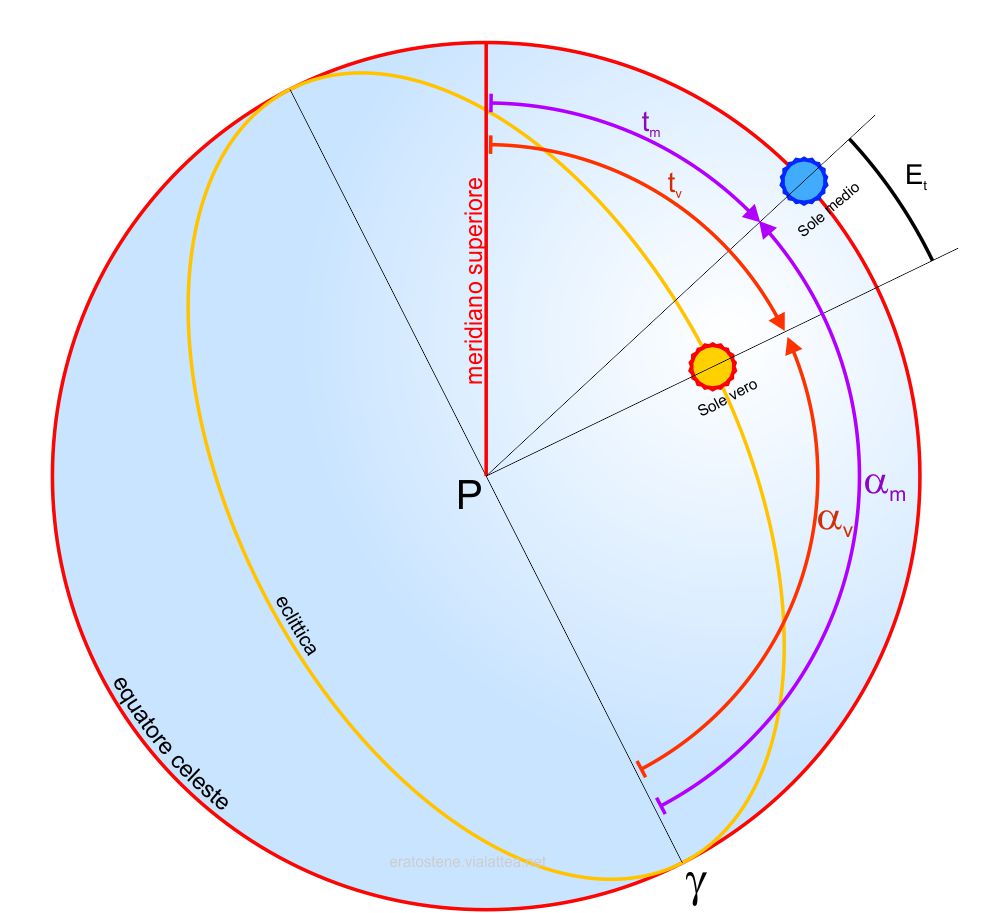
Lo schema qui a fianco rappresenta un diagramma orario dove $P$ è il polo nord celeste e $\gamma$ è il punto vernale. L’equazione del tempo $E_t$ può essere vista sia come la differenza tra gli angoli orari del Sole vero e del Sole medio, sia come la differenza tra l’ascensione retta del Sole medio ($\alpha_m$) e l’ascensione retta del Sole vero ($\alpha_v$).
$$E_t = t_v-t_m$$
e anche:
$$E_t = \alpha_m-\alpha_v$$
L’equazione del tempo, che si misura tradizionalmente in minuti, si annulla quattro volte l’anno: intorno alle date del 15 aprile, 15 giugno, 1° settembre e 25 dicembre. Assume valori estremi verso il 12 febbraio ($-14^m25^s$), il 15 maggio ($+3^m8^s$), il 27 luglio ($-6^m20^s$) e il 3 novembre ($+16^m24^s$).
In molti testi l’equazione del tempo è definita come $E_t = t_m-t_v$. In questo caso cambia solo il segno. Ogni tabella o grafico dovrebbe essere associato alla corretta definizione. Questa “doppia definizione” che potrebbe confondere, deriva dalla storia dell’uso che si è fatto di questo valore: quando non esistevano gli orologi meccanici l’equazione del tempo era la correzione da apportare alla lettura del tempo vero segnato dell’orologio solare per ottenere il tempo medio ($t_m=t_v+E_t$). A quest’ultimo erano interessati principalmente gli astronomi perché la vita civile era regolata dal tempo solare vero. Con il diffondersi degli orologi meccanici, i ruoli si sono invertiti: l’equazione del tempo è diventata la correzione da apportare al tempo medio per trovare la posizione simultanea del Sole vero ($t_v=t_m+E_t$).
Vedi: Tabella e grafici dell’equazione del tempo; come si calcola l’equazione del tempo.
- La misura del tempo: una introduzione
- Il diagramma orario
- Giorni e tempi
- Il giorno siderale e il tempo siderale
- Giorno siderale e giorno solare
- Il giorno solare non è un intervallo costante
- L’anno tropico e l’anno siderale
- L’introduzione del giorno solare medio: un intervallo di tempo costante
- L’equazione del tempo
- Giorno astronomico e giorno civile
- Il tempo e le differenze di longitudine
- Il tempo e l’ascensione retta
- Tempi locali e tempi del meridiano fondamentale
- Tempo meccanico e tempo dell’orologio solare
- Tempo medio, tempo siderale e conversioni
- L’irregolarità della rotazione terrestre e i tempi atomici
- Sole medio e Sole vero

