Si è visto nella pagina precedente che il tempo siderale, in qualche modo ci permette di misurare le differenze di longitudine tra gli osservatori. Le numerose applicazioni pratiche di questo fatto, sono dovute anche ad un’altra semplice e speciale relazione aritmetica che il tempo siderale $\theta$ ha con l’ascensione retta $\alpha$ e con il tempo $t$ di un astro.
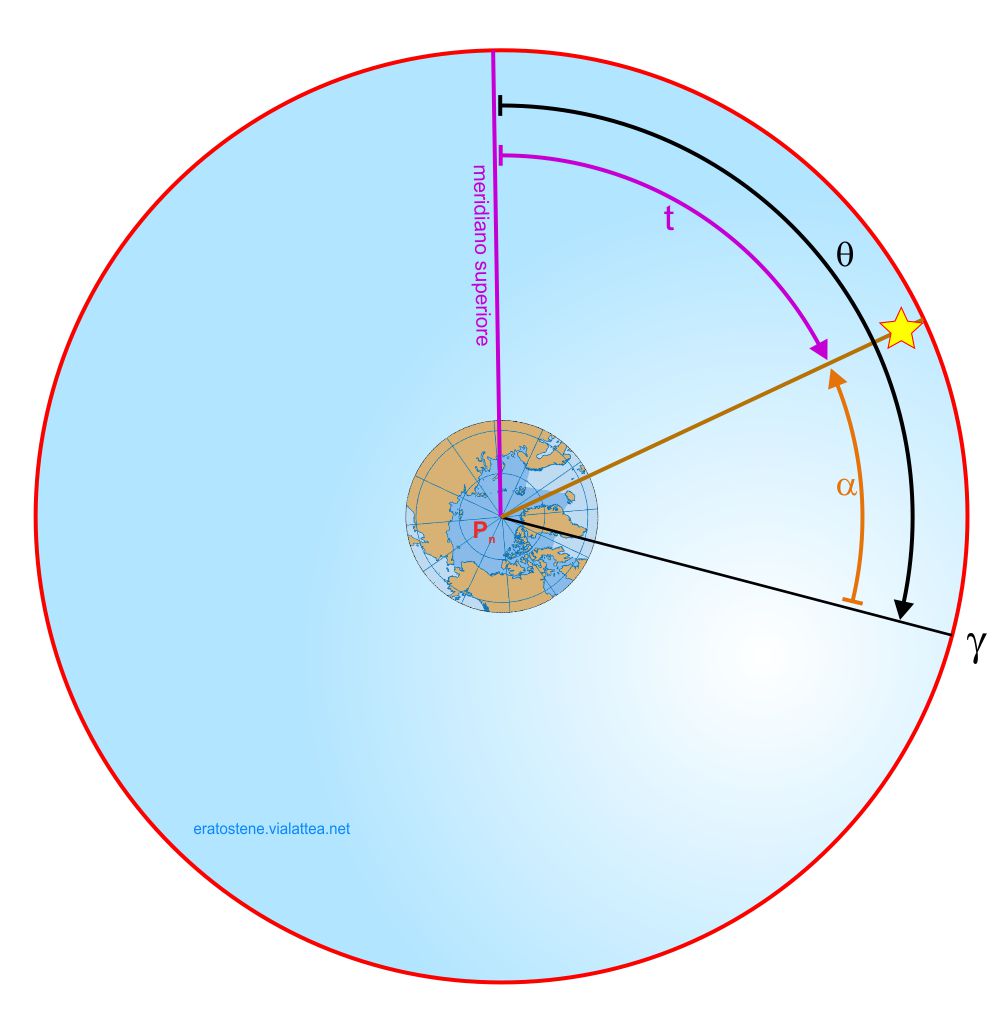
Osservando questo diagramma orario, si capisce facilmente come queste tre variabili sono legate tra loro; se dall’orario di una stella si aggiunge la sua ascensione retta, si ottiene il tempo siderale:
$$\boxed{\theta = t + \alpha}$$
Per rendere intuibile la rappresentazione di queste somme algebriche angolari sul diagramma orario, basta disegnare gli angoli (che sono sempre positivi) dotandoli di una freccia che indica in quale senso essi crescono. In questo caso l’ascensione retta cresce in senso antiorario, mentre il tempo dell’astro cresce in senso orario, come pure il tempo siderale.
Così, se un osservatore misura l’orario $t$ di una stella e se ne conosce l’ascensione retta $\alpha$ ricavandola da un almanacco, può calcolare il tempo siderale $\theta$.
Viceversa, se egli conosce il tempo siderale $\theta$ dell’istante dell’osservazione e l’ascensione retta $\alpha$ di una stella, potrà calcolarne l’angolo orario $t$ e quindi inclinare il suo telescopio nella direzione corretta per poterla osservare:
$$t=\theta – \alpha$$
Una terza possibilità è quella di calcolare l’ascensione retta $\alpha$ di un astro, conoscendo il tempo siderale $\theta$ dell’osservazione in cui ha misurato l’orario $t$ della stella:
$$\alpha =\theta-t$$
Per finire, quando una stella passa al meridiano superiore il suo tempo $t$ è zero, perciò la sua ascensione retta $\alpha$ diventa anche la misura del tempo siderale $\theta$:
$$\alpha = \theta$$
- La misura del tempo: una introduzione
- Il diagramma orario
- Giorni e tempi
- Il giorno siderale e il tempo siderale
- Giorno siderale e giorno solare
- Il giorno solare non è un intervallo costante
- L’anno tropico e l’anno siderale
- L’introduzione del giorno solare medio: un intervallo di tempo costante
- L’equazione del tempo
- Giorno astronomico e giorno civile
- Il tempo e le differenze di longitudine
- Il tempo e l’ascensione retta
- Tempi locali e tempi del meridiano fondamentale
- Tempo meccanico e tempo dell’orologio solare
- Tempo medio, tempo siderale e conversioni
- L’irregolarità della rotazione terrestre e i tempi atomici
- Sole medio e Sole vero

