Nella vita quotidiana chiamiamo giorno l’intervallo di tempo compreso tra una mezzanotte e la successiva e sappiamo che esso ha a che fare in qualche modo con il sorgere e il tramontare del Sole. In astronomia il giorno ha un significato molto più ampio e articolato. Il moto apparente diurno della sfera celeste, dovuto alla rotazione della Terra attorno al suo asse, fa sì che non solo il Sole ma tutti gli astri attraversino quotidianamente il cielo da oriente a occidente percorrendo degli archi circolari. Alcuni di essi sorgono e tramontano, altri troppo vicini al polo celeste elevato non tramontano mai e ruotano attorno ad esso lungo percorsi circolari compresi completamente nell’emisfero visibile. In ogni caso, tutti gli astri attraversano il meridiano superiore “regolarmente” una volta al giorno.
Il giorno dell’astro
l giorno in astronomia è un intervallo di tempo compreso tra due successivi passaggi di un astro allo stesso meridiano. Si parla quindi genericamente di astro, non di Sole. E l’espressione corretta è giorno dell’astro. Perciò ogni astro ha il suo giorno.
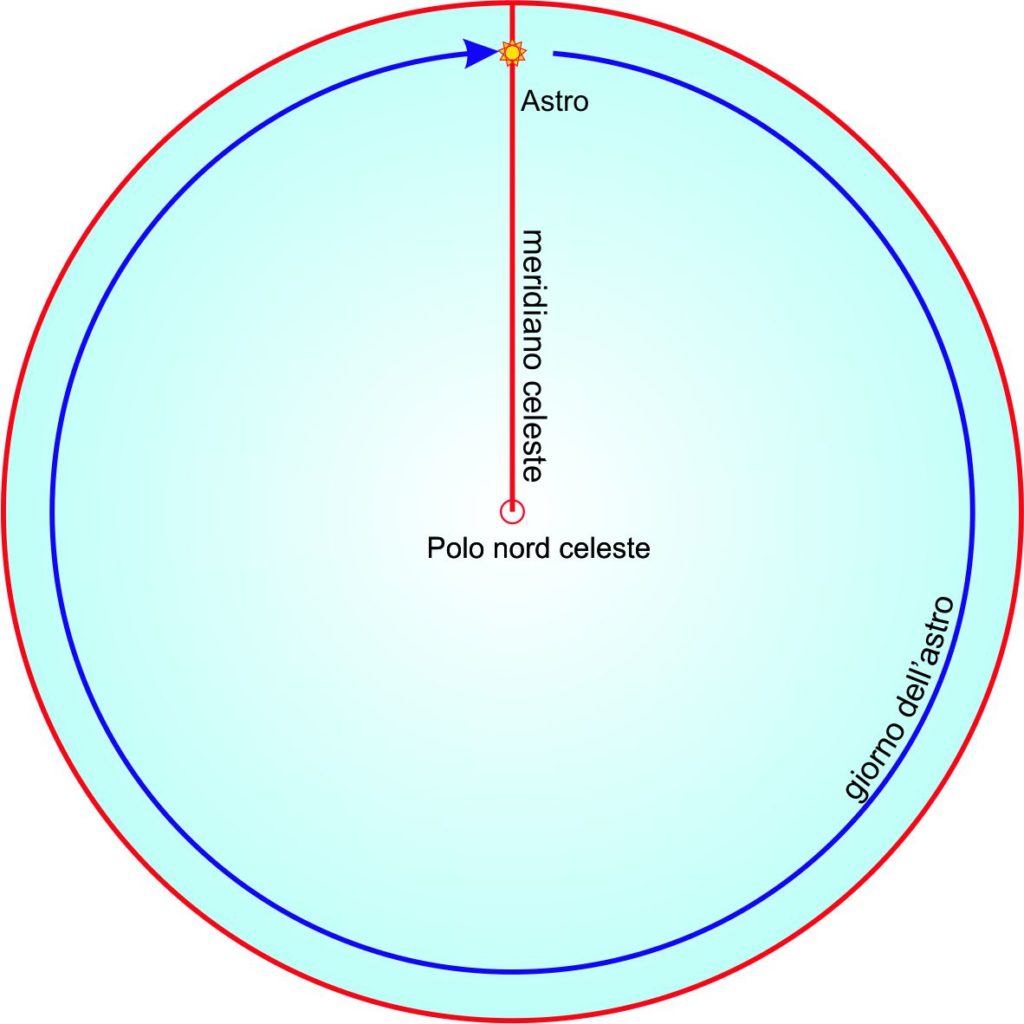
Così, ogni stella ha il suo giorno stellare; il giorno lunare è l’intervallo compreso tra due passaggi del centro del disco lunare al meridiano. L’intervallo tra due passaggi del centro del Sole è chiamato giorno solare vero. L’oggetto celeste che esegue una rivoluzione apparente attorno alla Terra può anche non essere un oggetto fisico bensì un punto astratto come ad esempio il punto vernale che è uno dei due nodi dell’eclittica. In particolare, l’intervallo tra due successivi passaggi al meridiano del punto vernale è chiamato giorno siderale.
In questo diagramma orario, è indicato con la freccia blu il percorso del moto diurno apparente di un astro tra due successivi passaggi al meridiano superiore. Il tempo impiegato per coprire questo percorso è il giorno dell’astro.
Perché così tanti tipi di giorni?
Se tutti gli astri ruotassero in modo solidale con il moto apparente della sfera celeste, i loro giorni sarebbero intervalli di tempo tutti identici tra loro. Esisterebbe un solo giorno: quello della sfera celeste stessa. Invece, come sappiamo, molti astri, in particolare il Sole, la Luna e i pianeti hanno un loro moto proprio più o meno evidente rispetto alla sfera celeste. La componente in ascensione retta del moto proprio di un astro determina la lunghezza del suo giorno. Così, il giorno di un astro con moto proprio talmente piccolo da essere trascurabile o addirittura irrilevabile agli strumenti, come ad esempio quello delle stelle molto lontane e delle galassie è un intervallo di tempo costante. Gli astri più vicini, in particolare il Sole, la Luna e i pianeti, hanno un rapido moto in ascensione retta e non si tratta mai di un moto uniforme: la velocità di cambiamento di ascensione retta varia continuamente. Di conseguenza il loro giorno non è un intervallo costante di tempo.
Il tempo di un astro
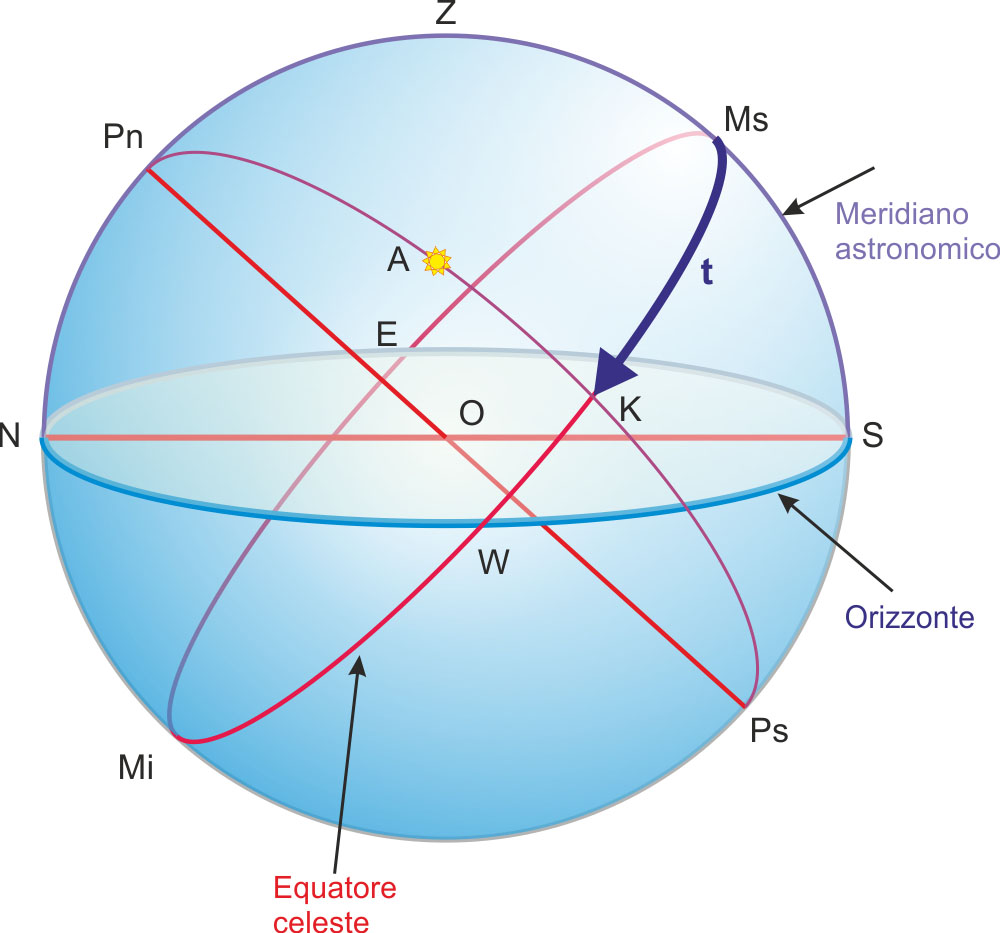
Un concetto strettamente legato al giorno è il tempo. Come esiste il giorno di un astro, così è stato definito il tempo di un astro in modo semplice e preciso: il tempo di un astro è il suo angolo orario (arco $t$ dell’immagine a fianco). Troviamo a questo proposito una serie di espressioni con significato uguale o molto simile: angolo orario dell’astro, ora dell’astro, tempo dell’astro, orario dell’astro. Quest’ultima espressione ha soprattutto un significato geometrico: l’orario è il semicircolo orario che passa per l’astro (nell’immagine qui a fianco $P_nAKP_s$). L’espressione orario dell’astro però è usata anche per intendere la misura del suo angolo orario.
Quando l’astro passa al meridiano inferiore, il suo tempo è $12^h$. Il tempo di un astro aumenta continuamente per ritornare a zero nell’istante in cui raggiunge le $24^h$, cioè al passaggio successivo al meridiano superiore. Così esiste il tempo solare vero o ora solare vera che è l’angolo orario del centro del disco solare, il tempo lunare, il tempo stellare. L’orario del punto vernale è chiamato tempo siderale o ora siderale.
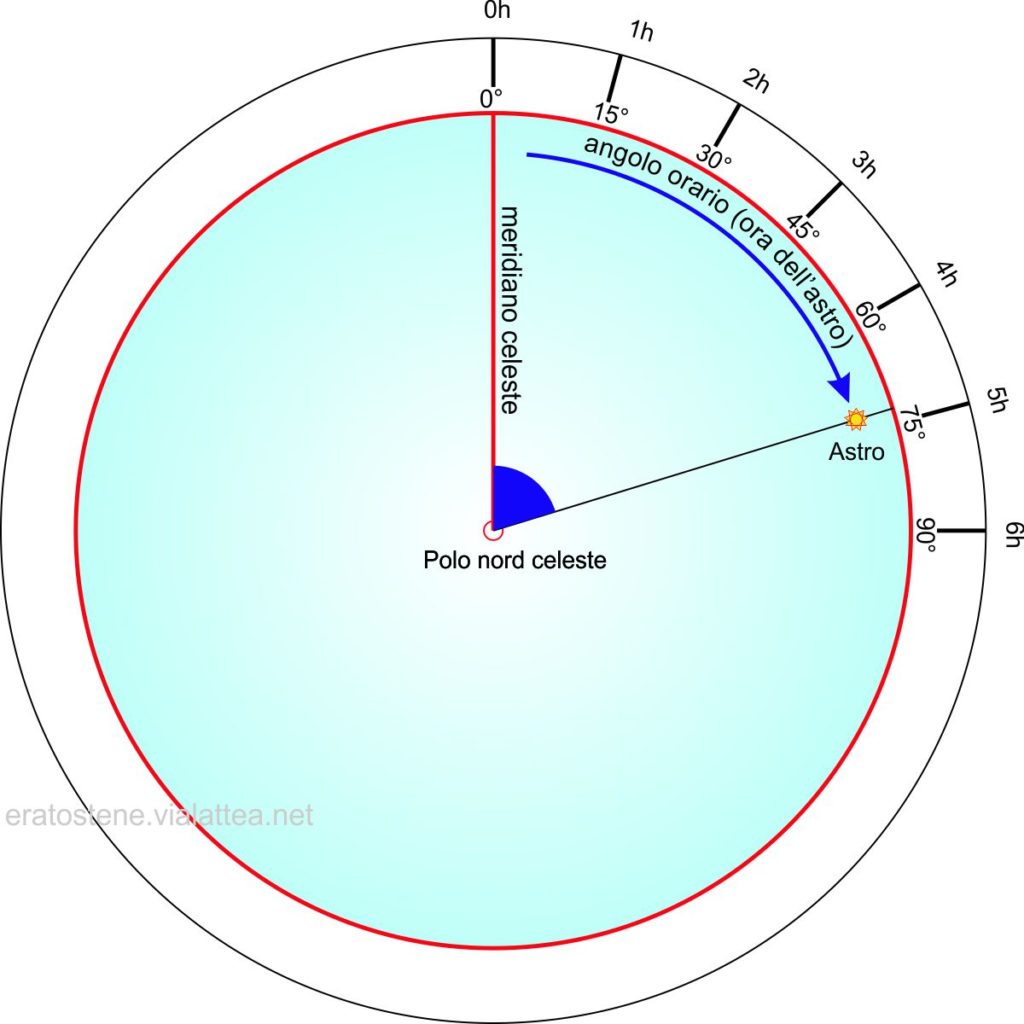
Un modo pratico per rappresentare il tempo di un astro è il diagramma orario. Il lettore capirà che la somiglianza tra lo schema del diagramma orario e il quadrante di un qualsiasi orologio meccanico non è così strana. Il diagramma orario è una rappresentazione della sfera celeste “appiattita” sul piano dell’equatore, quest’ultimo rappresentato dal cerchio rosso che fa da bordo. La lancetta di questo “orologio astrale” ha come perno il polo celeste elevato. Essa non è altro che la proiezione sul piano del semicircolo orario dell’astro e quindi assume la forma di un raggio del cerchio equatoriale. L’unica differenza sostanziale tra il diagramma orario e il nostro orologio da polso è la scala dei tempi che qui va da $0^h$ $24^h$ (o da $0^\circ$ a $360^circ$).
Giorni e scale di tempi
Il giorno di un astro qualsiasi può essere usato come unità di misura per costruire una scala di tempo. Il giorno siderale, ad esempio, può essere diviso in $24$ ore siderali, $1\,440$ minuti siderali e $86\,400$ secondi siderali. Queste unità hanno ampiezza diversa dalle unità corrispondenti ricavate ad esempio dal giorno solare vero. In ogni caso si può costruire una scala di tempo scegliendo il giorno di un astro e un’epoca di origine e contando quanti giorni e quante frazioni di giorno sono trascorse da essa. Si può costruire così un orologio meccanico che sia sincronizzato con il giorno dell’astro, un orologio in grado di imitare l’evento astronomico e riprodurlo fedelmente. Prendendo come esempio il giorno siderale, un orologio siderale ben costruiro segnerebbe sempre il tempo siderale indicando per ogni istante l’angolo orario effettivo del punto vernale. Ho volutamente ignorato di citare come esempio il giorno solare vero: la sua complessità sarà spiegata più avanti.
La scelta dell’astro adatto per costruire un sistema di misurazione dello scorrere del tempo dipende da alcune importanti considerazioni.
Primo: la durata del giorno dipende dalla velocità di rotazione apparente della sfera celeste ma anche dal moto proprio dell’astro nella sua componente in ascensione retta. Ad esempio, il Sole si muove in senso diretto rispetto alle stelle (moto apparente annuo) percorrendo poco meno di un grado di ascensione retta al giorno. Di conseguenza, se si confronta il giorno solare con il giorno di una lontana stella “fissa” il cui moto proprio è trascurabile rispetto al moto apparente annuo del Sole, scopriamo che il primo è di circa 4 minuti più lungo del secondo ($1^circ=4^m$). Il giorno lunare è ancora più lungo di quello solare perché l’ascensione retta della Luna aumenta di circa 50 minuti al giorno (corrispondenti a circa $13^\gradi$).
Secondo: se si trattasse solo di una questione di lunghezza del giorno dell’astro da scegliere, non sarebbe un grosso problema. La questione principale sta nella sua “costanza”. Se la componente in ascensione retta di un astro aumentasse uniformemente, il suo giorno avrebbe comunque una lunghezza costante. Nella realtà nessuno dei principali corpi celesti dotati di moto proprio varia uniformemente la propria ascensione retta. Né il Sole, né tantomeno la Luna e i pianeti si muovono di moto proprio costante.
Il dilemma della misura del tempo è sempre stato quello di cercare in natura o costruire uno strumento che possa produrre un fenomeno ciclico ripetibile, il cui periodo possa essere considerato come un intervallo di tempo “costante”. Gli intervalli scanditi da questo strumento possono così essere usati per misurare altri intervalli. Si è sempre immaginata l’esistenza di un “tempo assoluto” che scorre uniformemente e indipendente da qualsiasi fenomeno ciclico. Trovare in natura un fenomeno ciclico che possa imitare questo tempo assoluto, o meglio, costruire uno strumento in grado di sincronizzarsi con esso è stato lo scopo di millenni di ricerche astronomiche e meccaniche. Nel secolo scorso la Teoria della Relatività di Einstein dimostra che questo tempo assoluto non esiste. Attualmente la scala di tempo più affidabile che siamo stati in grado di produrre è quella del tempo atomico TAI.
Come si può valutare l’uniformità o meno del moto in ascensione retta di un astro? L’unico modo è quello di confrontarne la variazione nel tempo usando un sistema di misurazione del tempo che si ritenga valido, come ad esempio l’uso di un buon orologio meccanico o il confronto con la scala di tempo di un astro che si ritenga più affidabile. Sembra di avere a che fare con un gatto che si morde la coda, ma ci sono buone ragioni che ci fanno propendere verso la scelta “meno sbagliata”.
Ad esempio, lo scenario della sfera celeste è composto da due principali popolazioni di oggetti: ci sono da una parte le cosiddette “stelle fisse” che, ad una prima approssimazione, mantengono una configurazione stabile tra di loro, e dall’altra i corpi “vaganti” (come il Sole, la Luna e i pianeti) che invece presentano una estrema varietà di moti propri rispetto alle stelle fisse. Se si ha idea di costruire una scala di tempo affidabile, la scelta cade necessariamente sugli oggetti della popolazione stellare: il giorno di una stella è sicuramente un’unità di tempo più affidabile del giorno del Sole o di un pianeta. Se si analizza con maggiore accuratezza la popolazione di stelle fisse però, si scopre che le stelle più vicine a noi hanno un moto proprio più evidente rispetto a quelle lontane: è una questione di parallasse. Quali sono perciò i corpi celesti più “immobili”? La risposta è immediata: i più lontani da noi. Così, se dovessi scegliere un astro che mi garantisca la massima costanza del suo giorno sceglierei una galassia molto lontana come ad esempio MACS_1149-JD che dista $13\text{,2}$ milioni di anni luce dalla Terra. Questa galassia è sicuramente “immobile” e il suo giorno è un intervallo costante molto affidabile. Di fatto una sorta di controllo astronomico del tempo è effettivamente in atto. Il sistema di radiotelescopi del Very Long Base Interferometry (VLBI) è utilizzato per osservare costantemente la posizione di una serie di radiosorgenti molto lontane (quasar), tanto lontane e “immobili” da permetterci di misurare le minime variazioni nella velocità stessa di rotazione della Terra.
Tornando sulla Terra per riprendere i fili del nostro discorso pratico attorno al giorno dell’astro, si capirà che, nonostante la citata irregolarità del moto prioprio del Sole, una scala di tempo solare, basata sul giorno solare dovrebbe essere comunque la più adatta agli scopi pratici quotidiani, visto che sarebbe sincronizzata con quello che chiamiamo comunemente “giorno” e che scandisce le nostre attività. Sappiamo tutti che di fatto è così: i nostri orologi da polso sono ben sincronizzati con il susseguirsi dei giorni. Ma arrivare a questo non è stato né facile né rapido. Si affronteranno più avanti alcuni aspetti interessanti dell’elaborazione che ha subito nella storia il tempo solare.
Si affronteranno nella prossima pagina il giorno siderale e il tempo siderale, considerati tra i più affidabili in astronomia e utili per orientarsi nella “geografia” celeste.
Astro | giorno (unità di tempo) | angolo orario (scala di tempo) | lunghezza del giorno in secondi SI |
|---|---|---|---|
Sole vero | giorno solare vero | tempo solare vero | minima $86\,379^s$, massima $86\,430^s$ |
Sole medio | giorno solare medio | tempo solare medio | $86\,400^s$ |
Punto vernale | giorno siderale | tempo siderale | $\approx86\,164\text{,1}^s$ |
Luna | giorno lunare | tempo lunare | $\approx89\,400^s$ |
una galassia lontana | giorno stellare | tempo stellare | $86\,164\text{,0989}^s$ |
- La misura del tempo: una introduzione
- Il diagramma orario
- Giorni e tempi
- Il giorno siderale e il tempo siderale
- Giorno siderale e giorno solare
- Il giorno solare non è un intervallo costante
- L’anno tropico e l’anno siderale
- L’introduzione del giorno solare medio: un intervallo di tempo costante
- L’equazione del tempo
- Giorno astronomico e giorno civile
- Il tempo e le differenze di longitudine
- Il tempo e l’ascensione retta
- Tempi locali e tempi del meridiano fondamentale
- Tempo meccanico e tempo dell’orologio solare
- Tempo medio, tempo siderale e conversioni
- L’irregolarità della rotazione terrestre e i tempi atomici
- Sole medio e Sole vero

