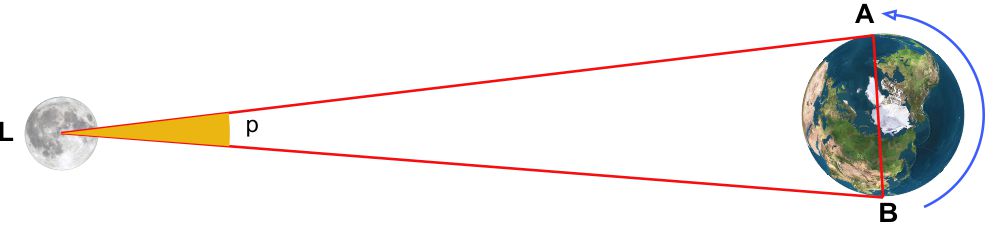
Questo schema rappresenta la Terra e la Luna non proporzionate per evidenti motivi (*). Due osservatori $A$ e $B$ si trovano alla massima distanza possibile tra loro in due punti diametralmente opposti del pianeta. Se confrontano le loro osservazioni simultanee scopriranno una sensibile differenza di posizione della Luna rispetto alle stelle di sfondo, pari all’angolo $p$.

La notevole base del triangolo parallattico $AB$ è tale da produrre un effetto di parallasse nell’osservazione dei corpi celesti più vicini come la Luna, i pianeti interni e il Sole. Essi presentano un angolo di parallasse misurabile anche con strumenti non molto sofisticati. Le stelle invece, a causa della loro grande distanza rispetto alla base $AB$, non subiscono alcun effetto di parallasse. Gli esempi riportati in questa pagina si riferiscono alla Luna per il semplice fatto che il nostro satellite naturale è il corpo celeste più vicino, quello che subisce un effetto di parallasse molto evidente, che potrebbe essere verificato anche confrontando tra loro due osservazioni ad occhio nudo.

Analizziamo ora la situazione geometrica e definiamo alcuni nuovi termini.

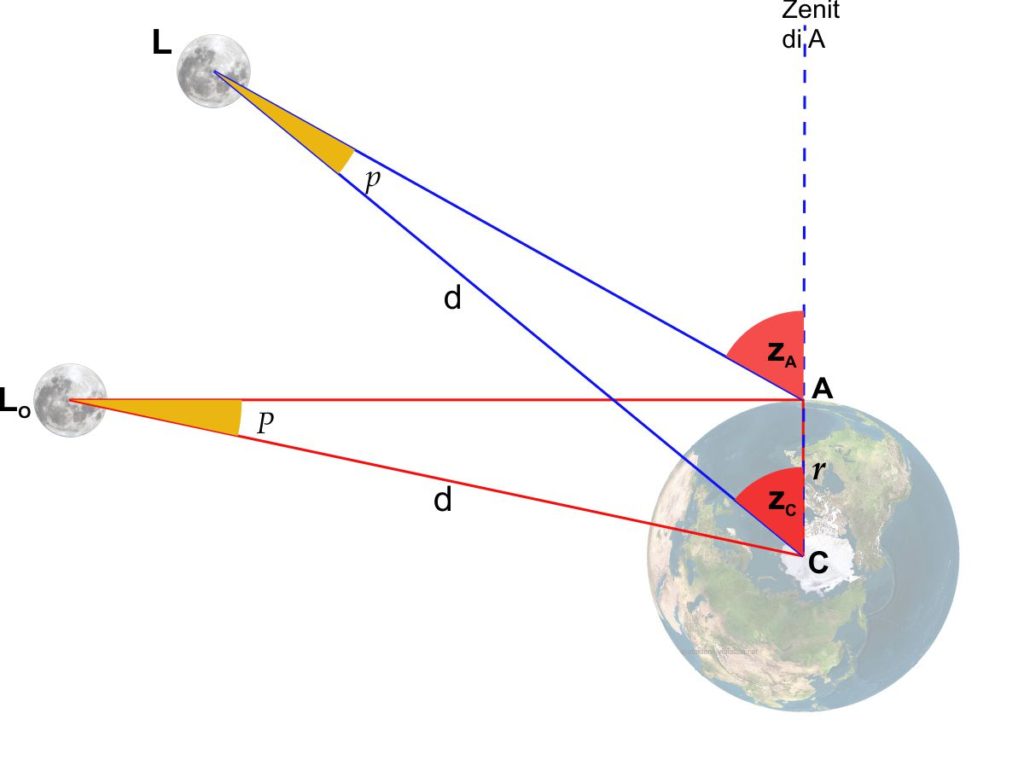
L’osservatore $A$ misura la distanza zenitale $z_A$ della Luna che si trova in posizione $L$. Un ipotetico osservatore al centro della Terra misurerebbe la distanza zenitale $z_C$ della Luna relativa allo stesso zenit di $A$. L’angolo$z_A$ è chiamato distanza zenitale topocentrica mentre l’angolo $z_C$ è la distanza zenitale geocentrica. La distanza zenitale topocentrica è anche detta apparente, mentre quella geocentrica è chiamata anche vera. Questi due valori corrispondono rispettivamente alla distanza zenitale che si misura su una sfera celeste centrata sull’osservatore $(z_A)$ e a quella misurata su una sfera celeste che ha per centro il centro della Terra $(z_C)$. L’angolo $z_A$ è sempre maggiore dell’angolo $z_C$ e la loro differenza $p$ è chiamata parallasse diurna.

\begin{equation}\tag{1}\label{eq1}
p = z_A – z_C
\end{equation}

(Osserviamo infatti che l’angolo $z_A$ è uno degli angoli esterni del triangolo $LAC$ per cui $p+z_C=z_A$ e quindi $p = z_A – z_C$).

Il nome parallasse diurna deriva dal fatto che, a causa della rotazione terrestre,  il suo valore varia con periodo uguale al periodo di rotazione, oscillando da un valore minimo a un valore massimo in funzione dell’altezza della Luna. Quando la Luna si trova al meridiano superiore, essa raggiunge la sua massima altezza e quindi la sua parallasse diurna è minima. Al contrario, quando l’astro sorge o tramonta è all’orizzonte e l’entità della parallasse diurna è massima. Se per un certo osservatore la Luna transita allo zenit, in quell’istante la sua parallasse diurna è nulla.

Consideriamo ora il triangolo $\widehat{L_{o}AC}$. La Luna in questo caso si trova in posizione $L_o$, cioè all’orizzonte dell’osservatore $A$. Un ipotetico osservatore che si trovasse al centro della Luna, vedrebbe il raggio terrestre sotteso dall’angolo $P$. Questo angolo di parallasse, chiamato parallasse orizzontale, è maggiore di $p$ e maggiore di qualsiasi altro valore di parallasse diurna corrispondente ad altre distanze zenitali della Luna diverse da $90^\circ$. Dato che il raggio equatoriale della Terra è leggermente maggiore del raggio polare, la situazione ottimale ideale sarebbe quella in cui sia la Luna che l’osservatore $A$ si trovassero sul piano dell’equatore. In questo caso si misurerebbe un angolo di parallasse chiamato parallasse orizzontale equatoriale.

Quest’ultimo valore rappresenta un termine di confronto per tutti i valori di parallasse misurabili da osservatori posti in qualsiasi altra località. E’ anche un termine di paragone per le parallassi di altri corpi del Sistema Solare. La parallasse orizzontale equatoriale media della Luna è notevole: $3\,422,7\text{”}$, corrispondente a circa $57$ primi d’arco, cioè quasi un grado. Per confronto, quella del Sole vale solo $\text{8,8”}$.

Relazioni tra parallasse diurna e orizzontale

Si consideri il triangolo $LAC$. Chiamiamo $r$ il raggio terrestre $AC$. Applicando il teorema dei seni e sapendo che il seno dell’angolo $z_A$ è uguale al seno del suo angolo supplementare $\widehat{LAC}$  possiamo scrivere:

\begin{equation}\tag{2}\label{eq2}
\frac{r}{\sin p} = \frac{d}{\sin z_A}
\end{equation}

Da questa equazione possiamo ricavare $\sin p$:

\begin{equation}\tag{3}\label{eq3}
\sin p = \frac{r}{d}\cdot\sin z_A
\end{equation}

D’altra parte il rapporto $\frac{r}{d}$ è anche uguale al seno dell’angolo $P$, cioè della parallasse orizzontale. Quindi l’equazione (3) può essere riscritta così:

\begin{equation}\tag{4}\label{eq4}
\sin p = \sin P\cdot\sin z_A
\end{equation}

Dato che i valori degli angoli di parallasse degli astri sono generalmente molto piccoli, si può applicare la regola dell’approssimazione degli angoli piccoli e scrivere:

\begin{equation}\tag{5}\label{eq5}
\boxed{p = P\cdot \sin z_A}
\end{equation}

dove sia $p$ che $P$ sono espressi in radianti.

Il valore della parallasse orizzontale $P$ è di circa $1^\circ$ e non è costante. La Luna, infatti, percorre un’orbita ellittica attorno alla Terra per cui la sua distanza varia da un valore minimo (al perigeo) di $56$ raggi terrestri, ad un valore massimo (all’apogeo) di $64$ raggi. I valori quotidiani di parallasse orizzontale della Luna e dei pianeti sono abitualmente tabulati negli almanacchi. Conoscendo il valore di $P$ e misurando $z_A$ si può determinare il valore della parallasse diurna $p$ dall’equazione (5) e quindi la distanza zenitale geocentrica $z_C$  dall’equazione (1). Conoscere $p$ significa sapere di quanto la Luna appaia “abbassata” rispetto alla sua altezza geocentrica vera. E’ da notare che l’effetto di parallasse è opposto all’effetto di rifrazione atmosferica il quale invece “alza” l’immagine dei corpi celesti che si trovano verso l’orizzonte. Nel caso della Luna, comunque, l’effetto di parallasse supera quello di rifrazione.

(*)

Se si dovessero rappresentare in proporzione la distanza Terra-Luna e i loro diametri, il risultato sarebbe questo:

L’angolo sotteso dal diametro della Terra, per un ipotetico osservatore lunare, è di $1^\circ54\text{‘}$ circa e la distanza Terra-Luna è uguale a circa $30$ diametri terrestri.