- Parallasse del viaggiatore
- Visione stereoscopica
- Il triangolo parallattico
- Uno stratagemma per misurare le distanze
- Parallasse diurna e orizzontale
- Misurare la distanza della Luna
- Un curioso fenomeno di parallasse
- Parallasse annua
- Diametri angolari degli astri
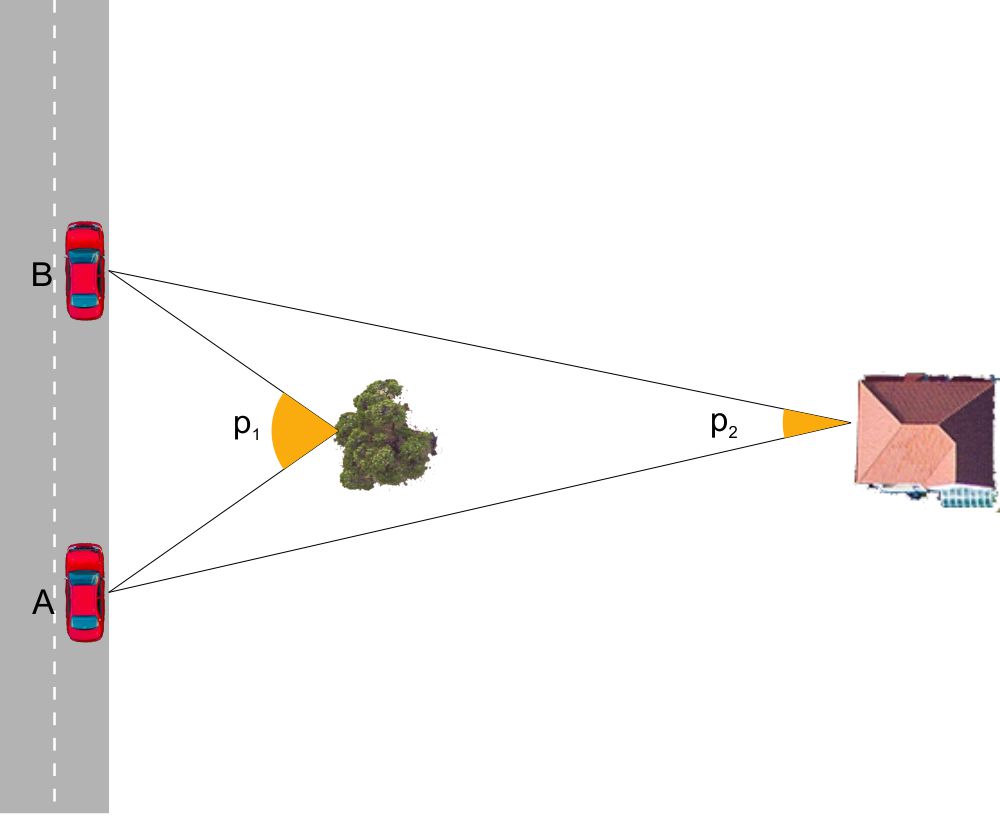 Durante un viaggio in automobile è esperienza comune quella di osservare dal finestrino in che modo gli elementi del paesaggio “si muovono” rispetto a noi e gli uni rispetto agli altri. Un albero che si trovano a poca distanza dalla strada passa rapidamente in senso opposto al moto dell’automobile. Un edificio più lontano sembra “passare” più lentamente. Le colline e i rilievi in lontananza sembrano quasi immobili. Solo dopo una osservazione prolungata ci accorgiamo che anch’essi si muovono rispetto a noi. Gli astri invece sembrano inseguirci: se l’auto ha un percorso rettilineo essi sono “fermi” davanti a noi, la linea di visuale conserva sempre la stessa direzione. Quando l’automobile passa dalla posizione A alla posizione B, la linea di visuale dell’albero cambia di direzione di un angolo $p_1$. La linea di visuale della casa, più lontana, cambia di direzione di un angolo minore $p_2$.
Durante un viaggio in automobile è esperienza comune quella di osservare dal finestrino in che modo gli elementi del paesaggio “si muovono” rispetto a noi e gli uni rispetto agli altri. Un albero che si trovano a poca distanza dalla strada passa rapidamente in senso opposto al moto dell’automobile. Un edificio più lontano sembra “passare” più lentamente. Le colline e i rilievi in lontananza sembrano quasi immobili. Solo dopo una osservazione prolungata ci accorgiamo che anch’essi si muovono rispetto a noi. Gli astri invece sembrano inseguirci: se l’auto ha un percorso rettilineo essi sono “fermi” davanti a noi, la linea di visuale conserva sempre la stessa direzione. Quando l’automobile passa dalla posizione A alla posizione B, la linea di visuale dell’albero cambia di direzione di un angolo $p_1$. La linea di visuale della casa, più lontana, cambia di direzione di un angolo minore $p_2$.
La velocità degli oggetti è tanto più piccola quanto maggiore è la loro distanza. La nostra stessa percezione istintiva della distanza degli oggetti dipende in parte da come ci appare il loro movimento, sia esso reale o relativo al nostro moto.
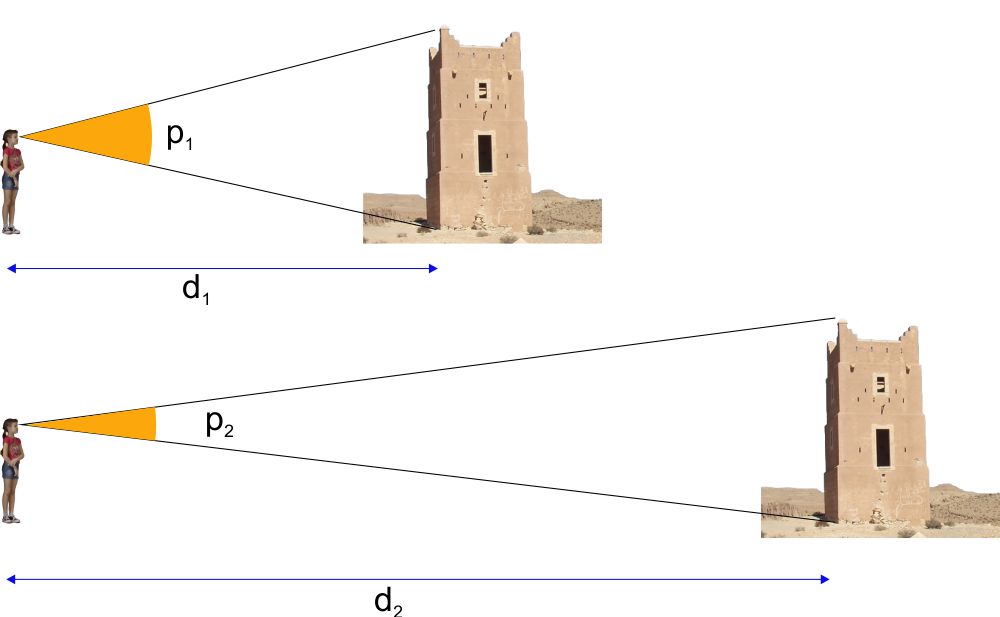 Un altro contributo alla nostra percezione delle distanze è dato dalle dimensioni angolari con cui ci appaiono gli oggetti. Ad esempio, l'”altezza angolare” di una torre è l’angolo compreso tra la direzione di visuale della sua base e quella della sua sommità. Questo angolo sarà tanto più piccolo quanto maggiore è la distanza tra noi e la torre. La nostra esperienza delle dimensioni reali delle torri in confronto alla loro altezza angolare ci suggerisce una stima istintiva della loro distanza.
Un altro contributo alla nostra percezione delle distanze è dato dalle dimensioni angolari con cui ci appaiono gli oggetti. Ad esempio, l'”altezza angolare” di una torre è l’angolo compreso tra la direzione di visuale della sua base e quella della sua sommità. Questo angolo sarà tanto più piccolo quanto maggiore è la distanza tra noi e la torre. La nostra esperienza delle dimensioni reali delle torri in confronto alla loro altezza angolare ci suggerisce una stima istintiva della loro distanza.

