In una notte di plenilunio si può fare il seguente esperimento: distendiamo il braccio verso la Luna e confrontiamo il suo diametro angolare con la larghezza del nostro indice. Si vedrà che la larghezza angolare del nostro dito (all’incirca $1^\circ)$ è il doppio del diametro angolare della Luna $(\simeq0.5^\circ)$. Ovviamente il diametro lineare della Luna è molto più grande della larghezza delle nostre dita, ma la Luna è anche molto più lontana.

Un esempio significativo di confronto tra i diametri angolari riguarda il Sole e la Luna. Il Sole ci appare con lo stesso diametro angolare della Luna. Questa coincidenza si osserva bene durante le eclissi di Sole, quando il disco della Luna copre più o meno esattamente il disco del Sole. Esso è in realtà quattrocento volte più grande del nostro satellite ma è anche quattrocento volte più lontano.
Nello schema a fianco, si rappresentano (in false proporzioni) l’occhio dell’osservatore $O$, la Luna e il Sole con i loro rispettivi diametri lineari $AB$ e $A’B’$. L’angolo $\theta$ rappresenta il diametro angolare dei due corpi celesti.
Possiamo notare che i due triangoli $OAB$ e $OA’B’$ sono simili tra loro perché sono isosceli e hanno l’angolo $\theta$ in comune. Perciò:
$$\frac{A’B’}{AB}=\frac{OA’}{OA}$$
In altre parole, il rapporto tra i diametri lineari del Sole e della Luna è uguale al rapporto tra le loro distanze dall’osservatore.
Sfruttando questo gioco di triangoli simili si possono stimare i diametri degli oggetti lontani di cui si conosca la loro distanza da noi. Gli astronomi, che misurano i diametri angolari generalmente molto piccoli dei corpi celesti, utilizzano una semplice formula che mette in relazione i seguenti parametri:
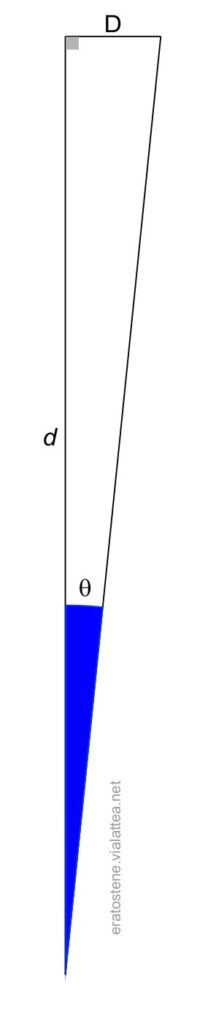
$D$: diametro lineare di un oggetto
$d$: distanza dell’oggetto (nella stessa unità di misura del diametro lineare $D$)
$\theta$: diametro angolare dell’oggetto, in secondi d’arco
$$\boxed{D = \frac{\theta \cdot d} {206\,265}}$$
La formula fa uso della regola dell’approssimazione dei piccoli angoli e funziona bene con oggetti molto piccoli o molto lontani. Osservando lo schema a fianco che rappresenta un triangolo rettangolo, la relazione trigonometrica fra $d$, $D$ e $\theta$ (espresso in radianti) è la seguente:
$\frac{D}{d}=tan\theta\simeq\theta$
Per esprimere $\theta$ in secondi d’arco, basta usare il fattore di conversione appropriato: $\text{1”}=1^{rad}/206\,265$. Ed ecco spiegata la formula.
Semidiametri
Spesso le dimensioni apparenti della Luna, del Sole e dei pianeti sono espresse utilizzando un parametro chiamato semidiametro ad $1$ unità astronomica di distanza ($s_0$). E’ il loro raggio angolare, espresso in secondi d’arco, così come ci apparirebbe alla distanza di una unità astronomica.
Semidiametro equatoriale | Semidiametro polare |
|
|---|---|---|
Sole | 959.63" | |
Luna | 2.396" | |
Mercurio | 3.36" | |
Venere | 8.34" (8.41")* | |
Marte | 4.68" | |
Giove | 98.44" | 92.06" |
Saturno | 82.73" | 73.82" |
Urano | 35.02" | |
Nettuno | 33.50" | |
Plutone | 2.05" |
Il vantaggio di questi parametri è che con una semplice divisione si possono prevedere le dimensioni con cui ci appariranno questi astri ($s$ in secondi d’arco) in base alla loro distanza ($\Delta$ in unità astronomiche).
$$s=\frac{s_0}{\Delta}$$

