- Parallasse del viaggiatore
- Visione stereoscopica
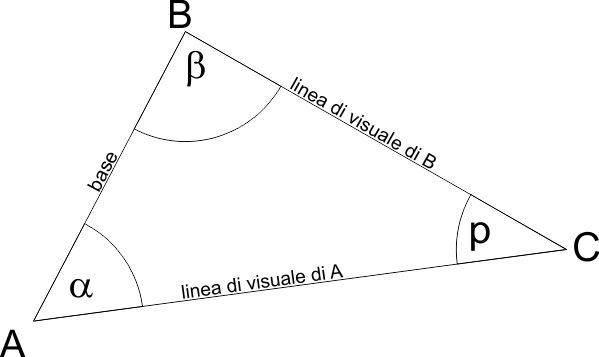
- Il triangolo parallattico
- Uno stratagemma per misurare le distanze
- Parallasse diurna e orizzontale
- Misurare la distanza della Luna
- Un curioso fenomeno di parallasse
- Parallasse annua
- Diametri angolari degli astri
$A$ e $B$ sono le posizioni di due osservatori e $C$ è l’oggetto osservato, l’angolo di parallasse $p$ è l’angolo \(\widehat{ACB}\) compreso tra le due linee di visuale. Il triangolo \(ABC\) è chiamato triangolo parallattico. I due osservatori possono misurare facilmente la distanza tra loro (chiamata base) e i due angoli \(\alpha\) e \(\beta\) compresi tra le linee di visuale e la base. Con questi tre elementi si può risolvere completamente il triangolo. Infatti, l’angolo di parallasse \(p\) si calcola per sottrazione da 180° (ricordiamo che gli angoli interni di qualsiasi triangolo sono supplementari):
$$p=180°-(\alpha+\beta)$$
Applicando poi il teorema dei seni si può calcolare sia la distanza \(\overline{AC}\) che la distanza \(\overline{BC}\):
$$\overline{AC} = \frac {\overline{AB}\sin \beta}{\sin p}$$
$$\overline{BC} = \frac {\overline{AB}\sin \alpha}{\sin p}$$