- Parallasse del viaggiatore
- Visione stereoscopica
- Il triangolo parallattico
- Uno stratagemma per misurare le distanze
- Parallasse diurna e orizzontale
- Misurare la distanza della Luna
- Un curioso fenomeno di parallasse
- Parallasse annua
- Diametri angolari degli astri
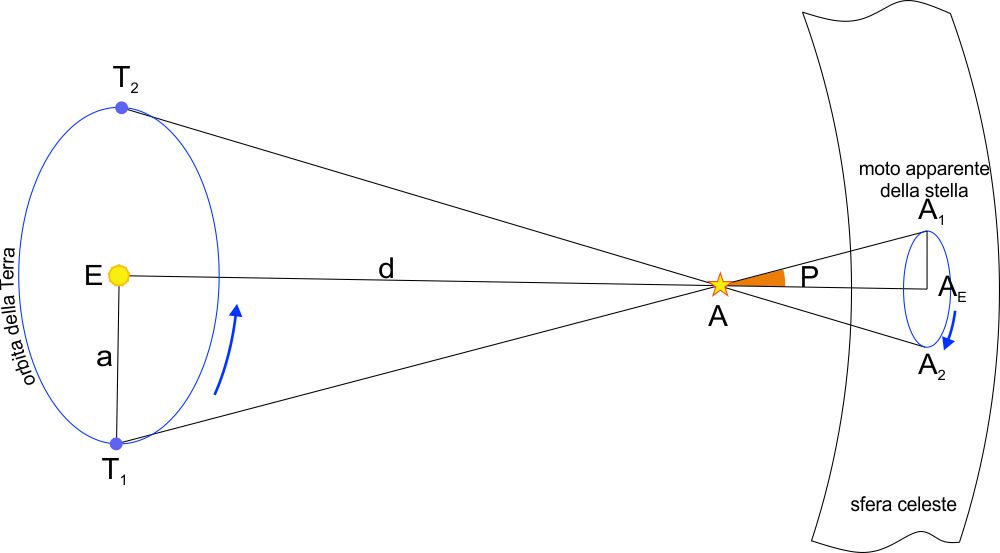
Se si osserva una stessa stella a distanza di sei mesi, i due punti di osservazione ($T_1$ e $T_2$) distano tra loro all’incirca $300$ milioni di chilometri, il “diametro” dell’orbita terrestre. Quando l’osservatore si trova in $T_1$ vede la stella $A$ nella posizione $A_1$ sulla sfera celeste. Dopo 6 mesi, l’osservatore si trova in $T_2$ e vede la stella $A$ in posizione $A_2$. Un ipotetico osservatore che si trovasse sul Sole $E$ vedrebbe la stella $A$ in posizione $A_E$.
Le stelle più vicine a noi presentano un cambiamento di posizione legato al moto annuo della Terra lungo la sua orbita. Il moto di rivoluzione della Terra produce in esse un “moto apparente” con traiettoria di forma ellittica sulla sfera celeste. Il centro di questa ellisse è la posizione della stella vista da un osservatore che si trova sul Sole (posizione eliocentrica). L’asse maggiore dell’ellisse è parallela all’eclittica. L’asse minore dipende dalla latitudine eclittica della stella. Se la stella si trova nei pressi dei poli dell’eclittica l’ellisse tende ad assumere la forma di una circonferenza. Se invece la stella si trova sul piano dell’eclittica, l’asse minore diventa nullo e l’ellisse si trasforma in un arco di eclittica.
Il raggio dell’orbita terrestre $\overline{ET_1}=a$ è l’Unità Astronomica ($au$) che equivale a circa $150$ milioni di chilometri.
L’angolo $P$ è chiamato parallasse annua della stella. E’ la dimensione angolare del raggio dell’orbita terrestre misurata da un ipotetico osservatore che si trovasse sulla stella.
Dato che la distanza della stella $d$ e il raggio dell’orbita terrestre $a$ sono due cateti di un triangolo rettangolo $AET_1$, la distanza della stella $d$ si calcola:
$$d=\frac{a}{\tan P}$$
Se l’angolo $P$ è espresso in radianti si può applicare l’approssimazione per angoli piccoli e scrivere:
$$d=\frac{a}{P}$$
Dato che un radiante equivale a $206265”$, se si esprime l’angolo di parallasse $P$ in secondi d’arco la formula diventa:
$$d = \frac{a\cdot 256265}{P}$$
Se si misura la distanza in unità astronomiche la formula si semplifica ulteriormente perché $a=1$ ma è scomodo perché risultano valori molti grandi. Si è così adottata una nuova unità di misura ad hoc, chiamata parsec ($pc$) che corrisponde alla distanza dalla quale si vedrebbe il raggio dell’orbita terrestre sottendere un angolo di un arcosecondo. Il parsec è uguale a $206256au$ per cui, alla fine si può scrivere:
$$d=\frac{1}{P}$$
dove la distanza $d$ è espressa in parsec e l’angolo di parallasse $P$ in secondi d’arco. Il parsec equivale a circa $3,26$ anni luce ($al$).
La stella più vicina a noi, Proxima Centauri, ha una parallasse annua di 0,7687 secondi d’arco. Ciò significa che la sua distanza è:
$$d= \frac{1}{0,7687”}=1,3009 pc = 4,243 al$$