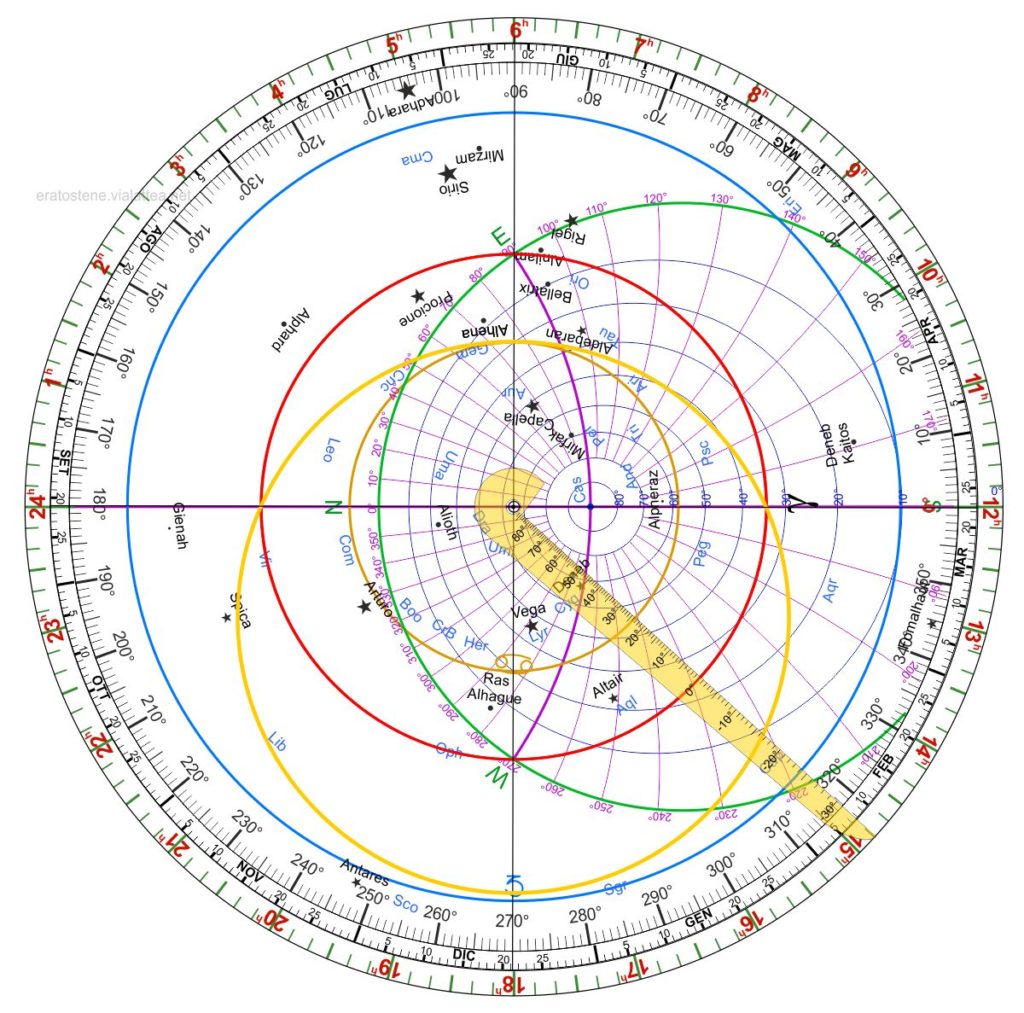
- Introduzione
- Descrizione generale
- Costruzione di un astrolabio semplificato
- Le basi della lamina: equatore e orizzonte
- Disegnare i tropici
- Gli almucantarat o cerchi di altezza
- I cerchi verticali
- La scala stereografica della declinazione
- La scala delle ore
- La rete: disegnare l’eclittica
- La scala dell’ascensione retta
- Disegnare le stelle
- L’astrolabio moderno: il circolo delle date
- La versione definitiva dell’astrolabio moderno
- Come si usa
- L’astrolabio tradizionale
- Rielaborazione dell’eclittica
yasmin karāmalakavad vidite viditaṃ bhaved viśvam
“Se conosci bene l’astrolabio, conoscerai l’universo come un frutto nel palmo della tua mano”
Rāmacandra Vājapeyin (1428)
L’astrolabio fu lo strumento astronomico più ampiamente usato nel Medioevo. Uno degli scopi dello strumento era osservazionale: era impiegato per trovare l’angolo del Sole, della Luna, dei pianeti o delle stelle rispetto all’orizzonte o rispetto allo zenit. Era usato anche per determinare l’altezza delle montagne e delle torri o le profondità dei pozzi o in agrimensura in generale. Molto più importante era, comunque, il suo valore come strumento di calcolo ausiliario. Esso permetteva agli astronomi di calcolare la posizione del Sole e delle stelle principali rispetto al meridiano e rispetto all’orizzonte allo scopo di trovare la latitudine e la direzione del nord, anche durante il giorno quando le stelle non erano visibili. Inoltre, permetteva loro di indulgere in quel prestigioso e lucrativo compito che era fare gli oroscopi. Prima che gli orologi affidabili fossero facilmente reperibili, l’astrolabio forniva al suo proprietario il mezzo per indicare l’ora, di giorno o di notte, fintantoché il sole o qualche stella riconoscibile segnata sullo strumento fosse visibile.
In questa prima parte descrivo la costruzione e l’uso dell’astrolabio planisferico nella sua versione “moderna”. In una seconda parte descriverò ulteriori componenti tipici di un astrolabio planisferico tradizionale.
La prossima pagina contiene la descrizione generale di un astrolabio storico.
La parola astrolabio deriva dal greco bizantino ἀστρολάβιον, composto da ἀστροον (astro) e λάβιον (catturo); i due termini ci offrono l’idea di uno strumento in grado di rappresentare (catturate) i tempi e le posizioni degli astri all’interno di una rete di coordinate.

*** Alcune pagine finali sono in costruzione o revisione ***

