Gli almucantarat o cerchi di altezza
I riferimenti altazimutali disegnati fino ad ora sono lo zenit e il cerchio dell’orizzonte. Arricchiamo ora questi riferimenti con i cerchi di altezza che sulla sfera celeste sono cerchi minori parallelli all’orizzonte. Nella proiezione ortografica sia l’orizzonte che i cerchi di altezza sono inclinati rispetto all’equatore. Di conseguenza, la loro proiezione stereografica assume le forme di una serie di circonferenze eccentriche. Disegniamone uno e si capirà come disegnare tutti gli altri. La tecnica è la stessa che abbiamo già visto per il disegno di un qualsiasi altro cerchio: segnare due estremità diametrali, proiettarle sul piano stereografico e trovare il punto medio del segmento che li congiunge.
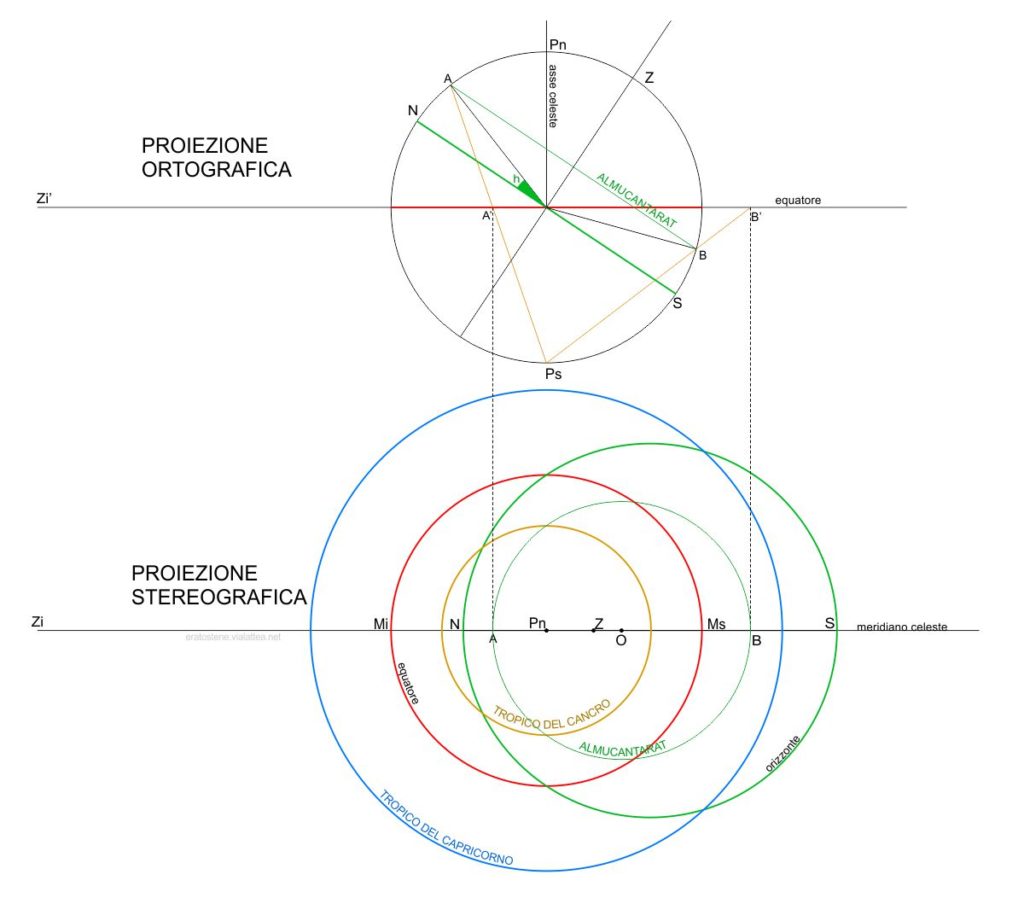
L’almucantarat rappresentato qui ha un’altezza di $h$ gradi rispetto all’orizzonte $NS$. Come si può notare anche dal disegno, il centro $O$ su cui puntare il compasso non coincide con il centro dell’orizzonte stereografico.
Lascio al lettore il calcolo del raggio e della posizione del centro di un almucantarat in funzione della sua altezza e della latitudine. Come esempio, suggerisco solo che la declinazione del punto $A$ è uguale alla colatitudine più l’altezza dell’almucantarat.
A seconda delle dimensioni dell’astrolabio, della precisione desiderata e della leggibilità, si può scegliere di disegnare solo $8$ almucantarat con altezza multipla di $10^\circ$ o aggiungere anche quelli intermedi a distanza di $5^\circ$, magari con un tratto più sottile.
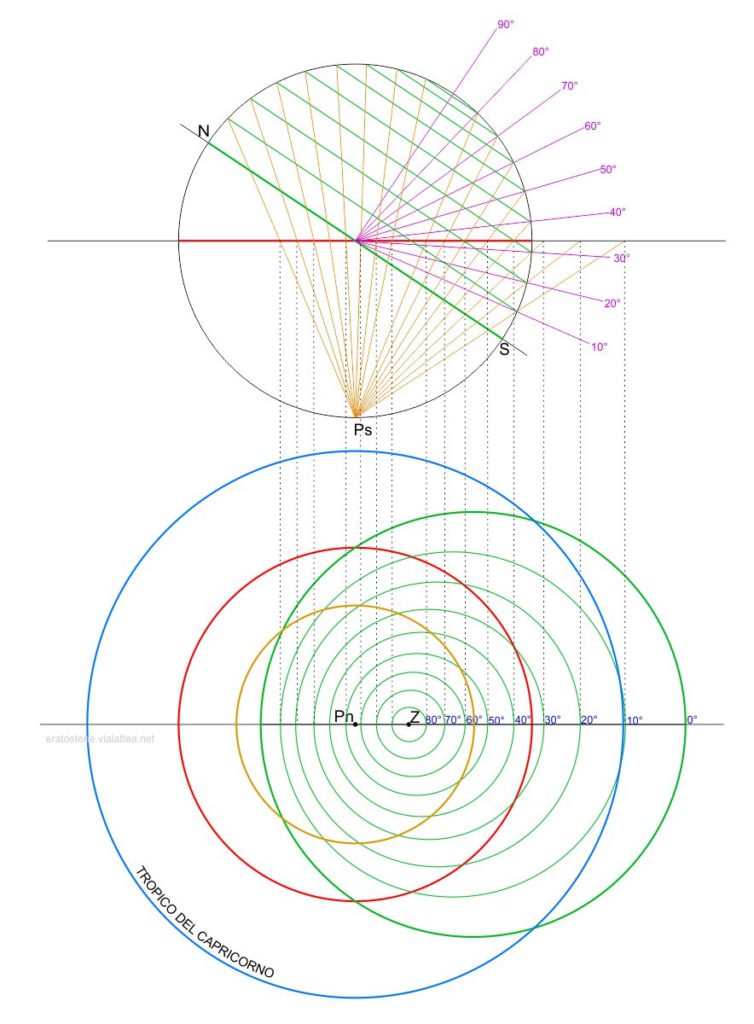
Ecco come si presenta la costruzione degli almucantarat multipli di $10^\circ$.
Nella prossima pagina si propone il metodo di costruzione dei circoli verticali.

