Le basi della lamina: equatore e orizzonte
La prima cosa da fare è un esperimento di dimensioni del disegno: bisogna tener presente che la proiezione stereografica di cui si fa uso per la costruzione di un astrolabio richiede uno “spazio di lavoro” molto più grande del risultato finale. Intendo dire che avremo bisogno di un foglio e di un compasso piuttosto grandi. La prima decisione da prendere riguarda le dimensioni finali dell’astrolabio. Un strumento troppo piccolo è difficile da disegnare con cura, uno molto grande richiede fogli e strumenti di disegno di dimensioni eccessive. Per decidere, come ho detto, si può fare un esperimento grafico che, con l’aiuto di alcuni semplici calcoli, servirà a introdurci alla conoscenza della proiezione stereografica, ma anche a capire quali sono le dimensioni massime che ci possiamo permettere con i mezzi a nostra disposizione.
Partiamo con la rappresentazione della sfera celeste in proiezione ortografica disposta in questo modo: l’asse celeste verticale, il piano dell’equatore rappresentato come una retta orizzontale e la circonferenza che rappresenta il meridiano celeste il cui piano giace sul piano del foglio. Il raggio $R$ di questa sfera è la misura da decidere in base ai disegni che faremo. Propongo come prima prova un raggio $R$ di $10$ centimetri. La decisione sulle dimensioni dello strumento definitivo dipenderà da una proporzione basata su questo primo disegno.
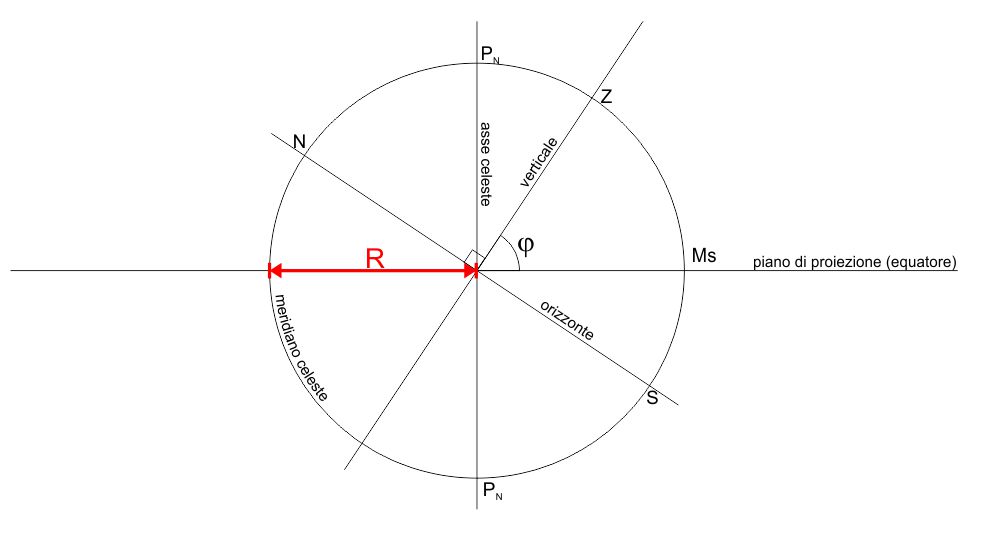
Il polo nord ($P_N$ e il polo sud $P_S$ celesti si trovano all’intersezione dell’asse celeste con la sfera. Si aggiunge ora il piano dell’orizzonte il quale, essendo perpendicolare al piano meridiano, è rappresentato come un diametro. L’inclinazione del piano dell’orizzonte rispetto all’equatore dipende dalla latitudine $\varphi$ del luogo in cui si utilizzerà l’astrolabio. Questa proiezone ortografica ha come punto di proiezione la direzione del punto cardinale est.
Perciò la linea est-ovest è perpendicolare al piano del foglio e si proietta come un punto al centro della sfera. Dell’orizzonte si vede la linea meridiana $NS$. Perpendicolare all’orizzonte è l’asse della verticale astronomica zenit-nadir $ZN_{ad}$. Sappiamo che la latitudine è l’angolo compreso tra il mezzocielo superiore $M_S$ e lo zenit $Z$; essa è uguale anche all’angolo compreso tra il polo elevato $P_N$ e il punto cardinale $N$ dell’orizzonte. Infatti è con questa inclinazione che saranno disegnati l’orizzonte e il suo asse.
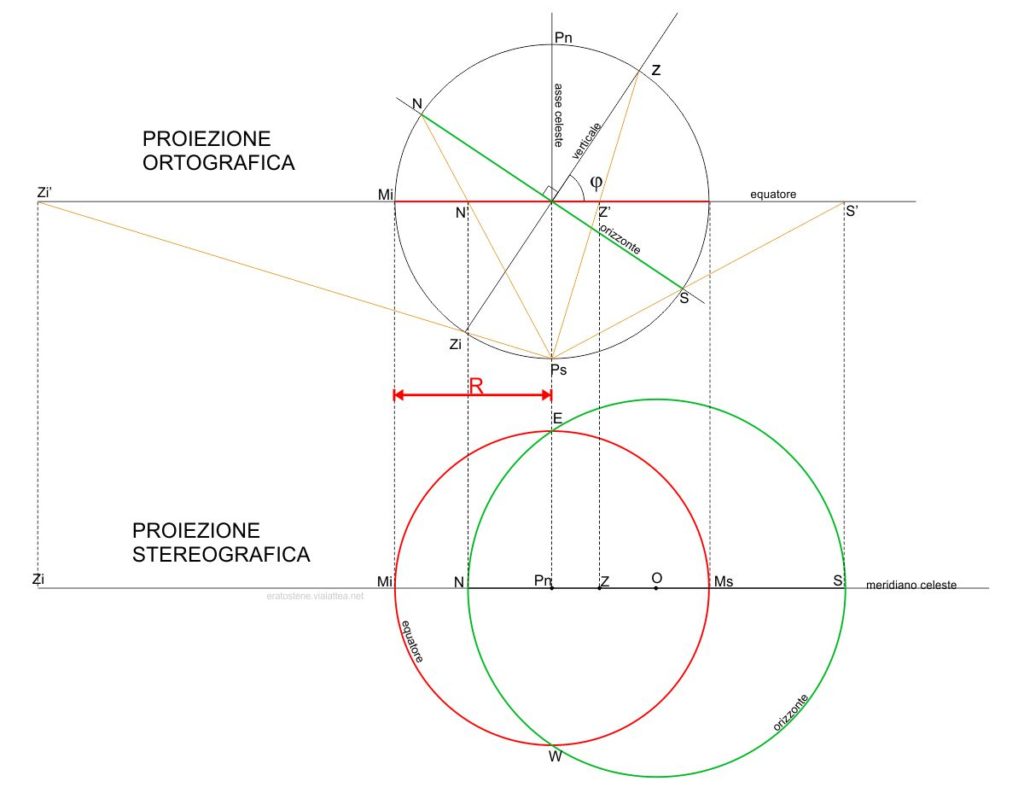
Al di sotto della proiezione ortografica appena descritta, si rappresenteranno i primi elementi in proiezione stereografica. Si sceglie come punto di proiezione il polo sud celeste $P_S$ e come piano di proiezione stereografica il piano dell’equatore.
La parte sottostante del disegno rappresenta infatti il piano dell’equatore coincidente con il piano del foglio . Si traccia innanzitutto una retta orizzontale che rappresenta la proiezione stereografica del meridiano celeste. Il meridiano diventerà l’asse di simmetria dell’astrolabio.
N.B.: La separazione delle due proiezioni che utilizzo in questo ed in altri esempi successivi non è necessaria, è solo un modo per rendere più comprensibile l’esposizione e per aumentare la chiarezza dei disegni che spesso sono piuttosto complessi; all’atto pratico, una volta compreso il significato e il meccanismo di proiezione, possiamo far coincidere il cerchio del meridiano e la retta dell’equatore della proiezione ortografica rispettivamente con il cerchio dell’equatore e con la retta del meridiano della proiezione stereografica. Si risparmia così il tracciamento di tutte le rette verticali parallele che collegano le due proiezioni e si evitano inutili fonti di errore.
L’equatore stereografico è identico alla circonferenza della sfera celeste: Lo si riproduce sotto, centrato in $P_N$ e di raggio $R$. Notiamo che i punti del mezzocielo, $M_s$ e $M_i$ coincidono nelle due proiezioni.
Per disegnare la posizione dello zenit che si trova sul piano meridiano si procede in questo modo:
– si traccia la retta $P_SZ$ e si individua il punto di intersezione $Z’$ sull’equatore
– si traccia la perpendicolare per $Z’$ che interseca il meridiano celeste sottostante nel punto $Z$ che è lo zenit stereografico.
Allo stesso modo si procede per qualsiasi altro punto e, come vedremo, anche per disegnare le stelle. Come ulteriore esempio, disegniamo ora il nadir stereografico:
– si congiunge il polo sud $P_S$ con il nadir ortografico $Z_i$: la retta va prolungata finché incontra l’equatore nel punto $Z_i’$.
– si scende con una perpendicolare da $Z_i’$ fino a incontrare il meridiano celeste nel punto stereografico del nadir $Z_i$.
Un po’ più complessa è la rappresentazione stereografica dell’orizzonte, ma il metodo, una volta appreso, si utilizzerà per tutti gli altri cerchi. Si procede in questo modo:
– si tracciano due rette $P_SN$ e $P_SS$ le quali incontrano l’equatore ortografico rispettivamente nei punti $N’$ e $S’$. Si scende con due perpendicolari fino a incontrare il meridiano stereografico nei rispettivi punti cardinali nord e sud $N$ e $S$. Questi sono i due punti diametrali dell’orizzonte stereografico perciò…
– si determina il punto medio $O$ del segmento $NS$. Questo punto è il centro dell’orizzonte stereografico: qui si punta il compasso, lo si apre con raggio $ON=OS$ e si traccia il circolo dell’orizzonte.
Osserviamo le due intersezioni tra l’orizzonte e l’equatore: sono i punti cardinali est e ovest. La retta che li congiunge è la linea est-ovest, perpendicolare alla linea meridiana.
Il nadir stereografico $Z_i$ è probabilmente il punto più lontano dal centro dell’equatore. Sarà tanto più lontano quanto maggiore è la latitudine $\varphi$. Anche se non rientrerà nei bordi dello strumento finale, è, come vedremo, un punto di costruzione importante per disegnare i circoli verticali. Alcuni circoli verticali richiederanno dei compassi molto grandi e la posizione del loro centro sarà molto lontana dal centro $P_N$ dell’equatore.
Approfittiamo qui per imparare ad utilizzare una semplice formula, spiegata nella pagina della proiezione stereografica, che ci permette di calcolare la distanza di un punto stereografico $X$ dal centro $P_N$ dell’astrolabio. Quelle che seguono non sono operazioni necessarie. Tutto può essere risolto esclusivamente per via grafica, ma il calcolo ci potrà essere utile in fase di progettazione, per decidere le dimesioni dell’astrolabio. Sapendo che la declinazione di un punto $X$ è $\delta$ e che il raggio dell’equatore è $R$:
$$\boxed{XP_N = R\tan\frac{90^\circ-\varphi}{2}}$$
Ad esempio, la distanza dello zenit $Z$ dal centro dell’astrolabio si calcola sapendo che la sua declinazione è uguale alla latitudine $\varphi$. Se la latitudine è $40^\circ$ e il raggio $R$ è $10 cm$, la distanza stereografica tra $Z$ e $P_N$ è:
$$ZP_N = 10 cm\cdot\tan\frac{90^\circ-40^\circ}{2}=\text{4,7 }cm$$
Come secondo esempio, calcoliamo ora la distanza del nadir $Z_i$ dal centro dell’astrolabio. La decliazione del nadir, è uguale alla latitudine $\varphi$, ma con segno negativo. Perciò:
$$Z_iP_N = 10cm\cdot\tan\frac{90^\circ-(-40^\circ)}{2}=\text{21,4 }cm$$
Con l’aiuito di un foglio elettronico ci si può divertire a calcolare queste due distanze in funzione della latitudine. Si scoprirà ad esempio che alle latitudini elevate il nadir stereografico si allontana parecchio dal centro dell’astrolabio mentre lo zenit si avvicina ad esso. Con $R=10 cm$, se la latitudine $\varphi=+80^\circ$, il nadir si trova a più di un metro di distanza, mentre lo zenit a meno di un centimetro.
Con l’aiuto della stessa formula calcoliamo ora i diametri dell’orizzonte stereografico e la distanza del suo centro $O$ rispetto al centro $P_N$ dell’astrolabio. Osserviamo che i punti cardinali nord $N$ e sud $S$ hanno le declinazioni uguali alla colatitudine e quindi rispettivamente: $+50^\circ$ e $-50^\circ$. Perciò le distanze dei punti stereografici $N$ e $S$ dal centro $P_N$ si calcolano:
$$NP_N=10 cm\cdot\tan\frac{90^\circ-50^\circ}{2}=\text{3,6 }cm$$
$$SP_N=10 cm\cdot\tan\frac{90^\circ-(-50^\circ)}{2}=\text{27,5 }cm$$
La distanza del centro $O$ dell’orizzonte da $P_N$ si calcola:
$$OP_N=\frac{27,5 cm+3,6 cm}{2}=\text{15,5 }cm$$
Il prossimo passo consiste nel disegno di due paralleli di declinazione notevoli: i tropici.

