Rielaborazione dell’eclittica
Come si è detto, l’equatorium solare permette di legare una data di calendario con la longitudine eclittica del Sole vero. Si tratta ora di suddividere l’eclittica disegnata sulla rete con una scala di longitudine che va da $0^\circ$ a $360^\circ$ partendo dal punto vernale e in senso antiorario. La suddivisione tradizionale consisteva nel tracciare i 12 settori dello zodiaco, di $30^\circ$ ciascuno. Il problema grafico principale è che l’eclittica sulla nostra proiezione stereografica è eccentrica rispetto all’equatore. Inoltre il centro geometrico dell’eclittica disegnata non coincide con il polo nord dell’eclittica. Di conseguenza i settori dei gradi di longitudine non uguale lunghezza e i meridiani di eclittica sono dei cerchi la cui costruzione è analoga alla costruzione dei circoli verticali di cui siamo già esperti. In realtà non si disegnano né i meridiani né i paralleli di eclittica che complicherebbero notevolmente l’aspetto complessivo della rete. Ciò che interessa a noi è trovare facilmente i punti della scala di longitudine lungo l’eclittica.
La costruzione grafica per trovare i punti di longitudine è piuttosto complessa e ricalca il metodo dei circoli verticali che già conosciamo. A scopo di curiosità, propongo qui un esempio che riguarda il procedimento per trovare il primo punto dei Gemelli, cioè il punto dei $60^\circ$ di longitudine eclittica.

Si traccia innanzitutto l’asse dell’eclittica inclinata di $\text{23,4}$ rispetto all’asse polare individuando così i poli $\pi_n$ e $\pi_s$ dell’eclittica. Si tracciano poi due rette: una che passa per $P_s\pi_n$ individuando la proiezione stereografica $\pi_n’$ del polo nord dell’eclittica sul piano equatoriale, e l’altra che passa per $P_s\pi_s$ e che individua la proiezione $\pi_s’$ del polo sud.
Si individua ora il punto medio $C$ tra le proiezioni dei due poli. La retta perpendicolare alla linea dei poi che passa per $C$ è l’asse comune a tutti i centri dei meridiani di eclittica.
Il nostro esempio intende individuare il punto di longitudine $60^\circ$ sull’eclittica. Perciò si apre un angolo di $60^\circ$ che ha per vertice $\pi_n’$ partendo dal lato $\pi_n’C$. Il secondo lato dell’angolo interseca la perpendicoare per $C$ sul punto $T$. Quest’ultimo è il centro in cui puntare il compasso per tracciare la circonferenza del meridiano di eclittica che passa per $\pi_n’$. Questo arco di circonferenza incontra l’eclittica nei punti $O$ e $Q$. Il punto $O$ il punto cercato di longitudine $60^\circ$ e il punto $Q$ è quello opposto, di longitudine $60^\circ+180^\circ=240^\circ$.
L’aspetto interessante di questa costruzione consiste nel verificare che il punto di $60^\circ$ di longitudine sull’eclittica un valore di ascensione retta di $\text{57,8}^\circ$ e che quello di $240^\circ$ ha ascensione retta di $\text{237,8}^\circ$. Se si porta la linea di fede su $PO$ e su $PQ$ si legge il valore della loro ascensione retta. Una verifica matematica consiste nell’usare la formula:
$$\tan{\alpha}=\frac{\sin\lambda\cdot \cos\epsilon}{\cos\lambda}$$
dove $\lambda$ è la longitudine di un punto dell’eclittica, $\epsilon=\text{23,4}^\circ$ è l’obliquità dell’eclittica e $\alpha$ è l’ascensione retta di quel punto.
Questa formula è la semplificazione di una formula generica che permette il calcolo dell’ascensione retta dalle coordinate eclittiche. Usando il computer o una calcolatrice suggeriamo di calcolare $\alpha$ utilizzando la funzione denominata solitamente “arctan2” o “atan2” che richiede due parametri (il numeratore e il denominatore della formula precedente) e individua il quadrante corretto dell’ascensione retta:
$\alpha=\text{arctan2}(\sin\lambda\cdot \cos\epsilon, \cos\lambda)$
Se ci si accontenta di tracciare una tacca ogni $5^\circ$ di longitudine può risultare comoda la seguente tabella che elencate le longitudini ad intervalli di $5^\circ$ e le corrispondenti ascensioni rette in gradi, calcolate con la formula descritta. Se invece desideriamo tracciare tutti i 360 punti della scala possiamo consultare una tabella completa.
Casa dello zodiaco | Longitudine | Ascensione retta |
|---|---|---|
Ariete | 0 | 0 |
5 | 4.6 |
|
10 | 9.2 |
|
15 | 13.8 |
|
20 | 18.5 |
|
25 | 23.2 |
|
Toro | 30 | 27.9 |
35 | 32.7 |
|
40 | 37.6 |
|
45 | 42.5 |
|
50 | 47.6 |
|
55 | 52.7 |
|
Gemelli | 60 | 57.8 |
65 | 63.1 |
|
70 | 68.4 |
|
75 | 73.7 |
|
80 | 79.1 |
|
85 | 84.6 |
|
Cancro | 90 | 90 |
95 | 95.4 |
|
100 | 100.9 |
|
105 | 106.3 |
|
110 | 111.6 |
|
115 | 116.9 |
|
Leone | 120 | 122.2 |
125 | 127.3 |
|
130 | 132.4 |
|
135 | 137.5 |
|
140 | 142.4 |
|
145 | 147.3 |
|
Vergine | 150 | 152.1 |
155 | 156.8 |
|
160 | 161.5 |
|
165 | 166.2 |
|
170 | 170.8 |
|
175 | 175.4 |
|
Bilancia | 180 | 180 |
185 | 184.6 |
|
190 | 189.2 |
|
195 | 193.8 |
|
200 | 198.5 |
|
205 | 203.2 |
|
Scorpione | 210 | 207.9 |
215 | 212.7 |
|
220 | 217.6 |
|
225 | 222.5 |
|
230 | 227.6 |
|
235 | 232.7 |
|
Sagittario | 240 | 237.8 |
245 | 243.1 |
|
250 | 248.4 |
|
255 | 253.7 |
|
260 | 259.1 |
|
265 | 264.6 |
|
Capricorno | 270 | 270 |
275 | 275.4 |
|
280 | 280.9 |
|
285 | 286.3 |
|
290 | 291.6 |
|
295 | 296.9 |
|
Aquario | 300 | 302.2 |
305 | 307.3 |
|
310 | 312.4 |
|
315 | 317.5 |
|
320 | 322.4 |
|
325 | 327.3 |
|
Pesci | 330 | 332.1 |
335 | 336.8 |
|
340 | 341.5 |
|
345 | 346.2 |
|
350 | 350.8 |
|
355 | 355.4 |
La suddivisione dell’eclittica con la scala della longitudine avrà questo aspetto.
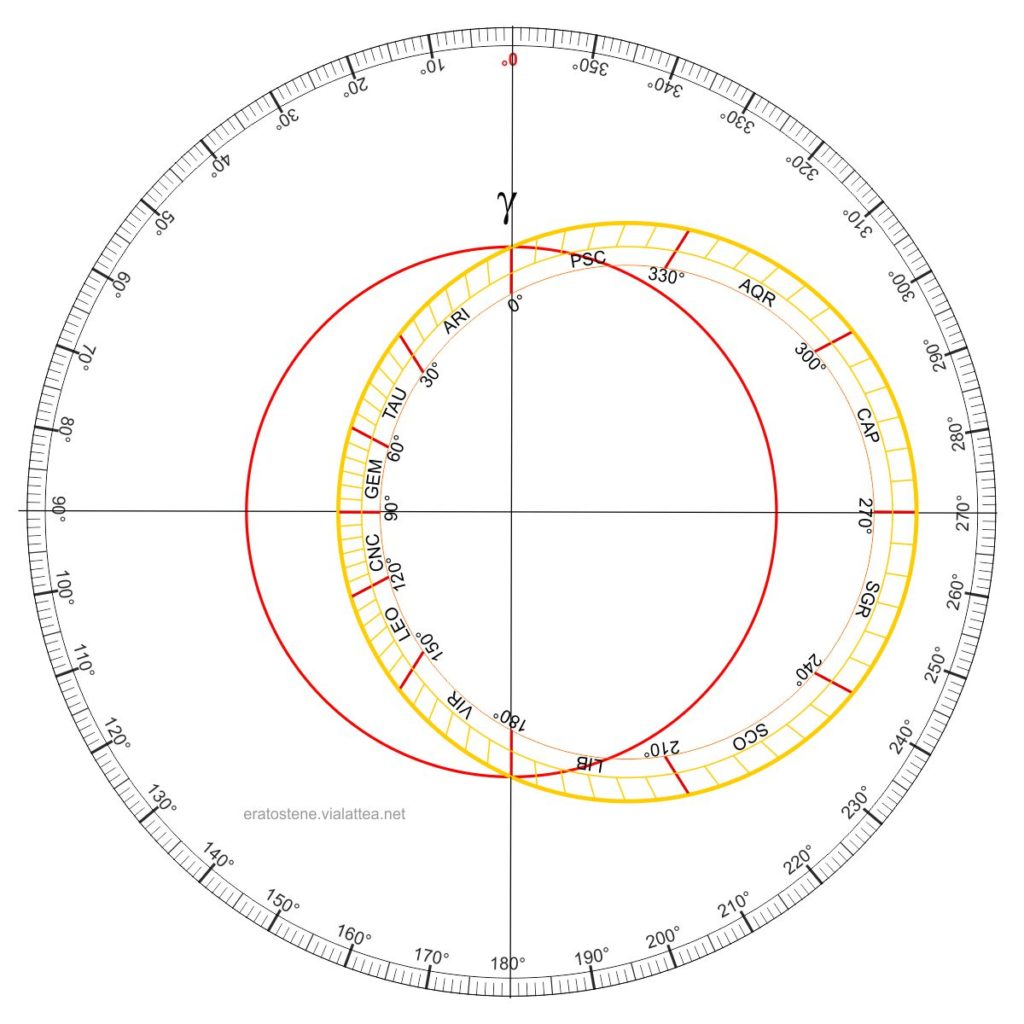
Come si nota, il circolo esterno è l’eclittica e la scala è costruita su una fascia interna. Le tacche sono inclinate perché si direzionano verso il centro dell’astrolabio, cioè verso il polo nord celeste. In tal modo la linea di fede, che rappresenta i semicircoli orari, si allinea ad esse.
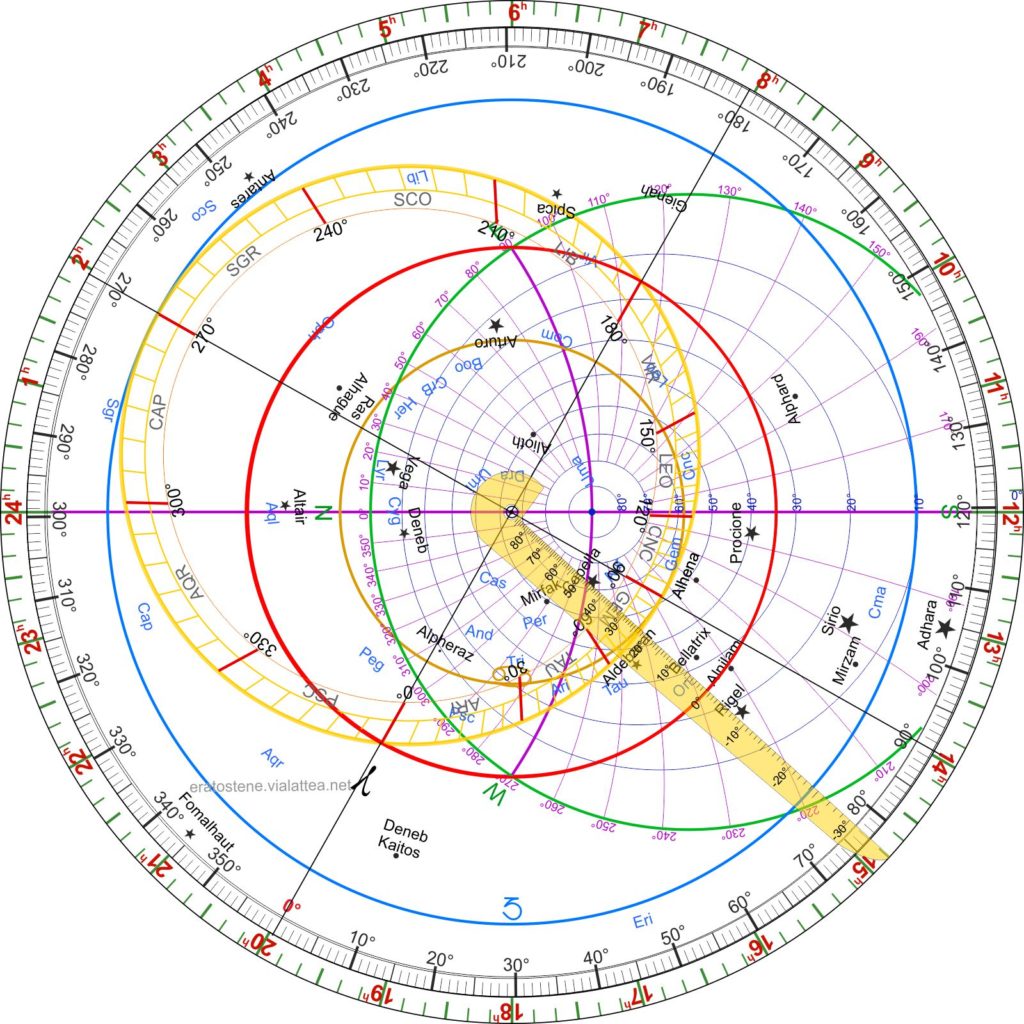
Questo è l’aspetto definitivo dell’astrolabio tradizionale con i suoi livelli sovrapposti.

