Alcuni dei nostri esperimenti pratici riguradanti la posizione del Sole richiedono di poter calcolare l’ascensione retta $\alpha$ o la declinazione $\delta$ del Sole che si trova sull’eclittica alla longitudine $\lambda$.
Le due semplici formule che useremo sono:
$$\boxed{\sin{\delta}=\sin{\lambda}\cdot\sin{\epsilon}}$$
$$\boxed{\tan{\alpha}=\tan{\lambda}\cdot\cos{\epsilon}}$$
dove $\epsilon$ è l’obliquità dell’eclittica che attualmente vale $23^\circ26’$
Le due formule precedenti sono semplificazioni delle formule di trasformazione tra le coordinate eclittiche (longitudine $\lambda$ e latitudine $\beta$) e quelle equatoriali (ascensione retta $\alpha$ e declinazione $\delta$):
$$\tan\alpha=\frac{\sin\lambda\cdot\cos\epsilon-\tan\beta\cdot\sin\epsilon}{\cos\lambda}$$
$$\sin\delta=\sin\beta\cdot\cos\epsilon+\cos\beta\cdot\sin\epsilon\sin\lambda$$
In entrambi i casi la latitudine eclittica $\beta$ è uguale a zero perciò le due formule si semplificano ponendo $\tan\beta=0$, $\sin\beta=0$ e $\cos\beta=1$.
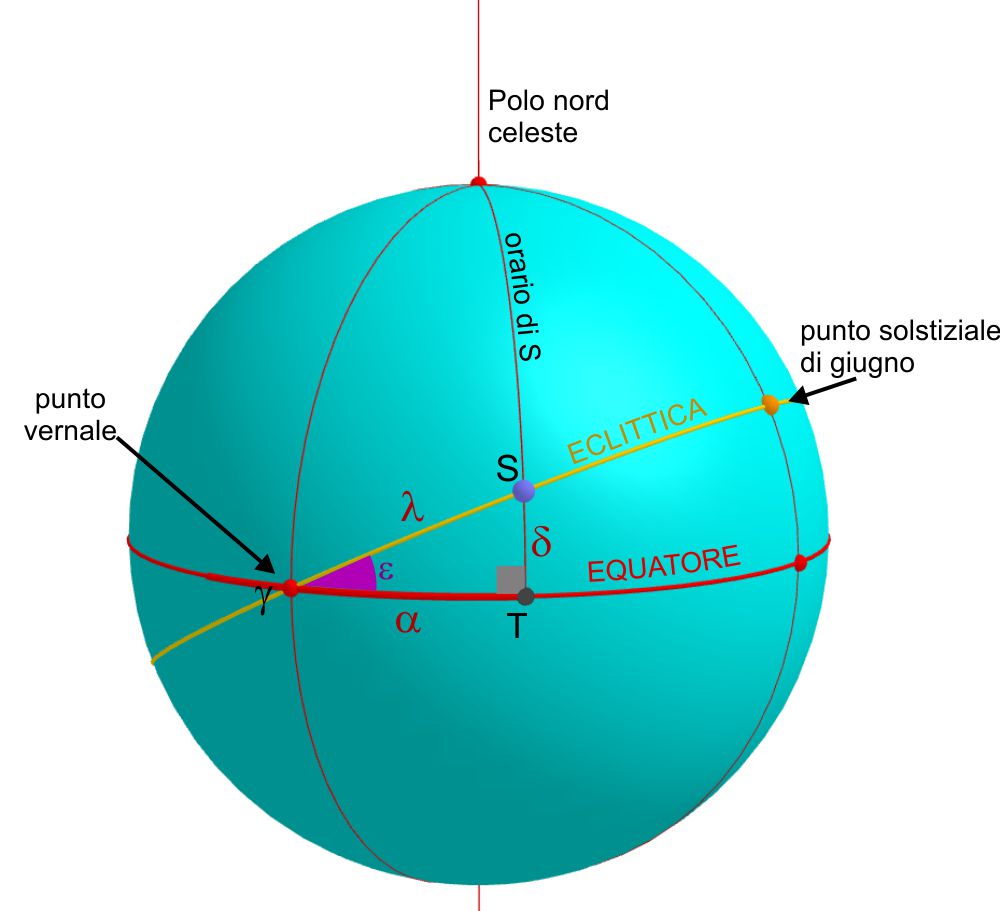
Come curiosità matematica, queste due formule si possono ricavare anche risolvendo un triangolo rettangolo sferico. Ecco le dimostrazioni, per chi è interessato.
L’immagine a fianco rappresenta l’eclittica, l’equatore e il punto vernale $\gamma$ che è uno dei dei due punti di intersezione di questi cerchi. L’angolo $\epsilon$ è l’obliquità dell’eclittica il cui valore è noto e varia di molto poco nel corso degli anni e dei secoli. Se il Sole si trova in $S$, l’arco $\gamma S$ è la sua longitudine eclittica. Il semicerchio orario del Sole incontra l’equatore nel punto $T$. Perciò l’arco $ST$ è la sua declinazione $\delta$, mentre l’arco di equatore $\gamma T$ è l’ascensione retta $\alpha$ del Sole.
Il triangolo $\gamma S T$ è un triangolo rettangolo sferico. L’angolo retto è quello al vertice $T$ perché gli orari sono perpendicolari all’equatore. Se vogliamo calcolare $\delta$ in funzione di $\lambda$ possiamo utilizzare il teorema dei seni che afferma l’uguaglianza dei rapporti tra i seni degli archi e i seni dei loro angolo opposti. L’arco $\delta$ è opposto all’angolo $\epsilon$ e l’arco $\lambda$ è opposto all’angolo retto in $\widehat{T}$. Perciò:
$$\frac{\sin{\delta}}{\sin{\epsilon}}=\frac{\sin{\lambda}}{\sin{90^\circ}}$$
Sapendo che $\sin{90^\circ}=1$, ricaviamo $\sin{\delta}$:
$$\boxed{\sin{\delta}=\sin{\lambda}\cdot\sin{\epsilon}}$$
La seconda formula si può dimostrare applicando una delle regole di Nepero sul triangolo rettangolo sferico. Il coseno di $\epsilon$ è uguale al prodotto della cotagente dell’ipotenusa $\lambda$ per la cotangente del complemento del cateto $\alpha:$
$\cos{\epsilon}=cot{\lambda}\cdot\cot{(90^\circ-\alpha)}$
$\,\,\,=cot{\lambda}\cdot\tan{\alpha}$
$\,\,\,=\frac{\tan{\alpha}}{\tan{\lambda}}$
Perciò, ricavando $\tan{\alpha}$:
$$\boxed{\tan{\alpha}=\tan{\lambda}\cdot\cos{\epsilon}}$$

