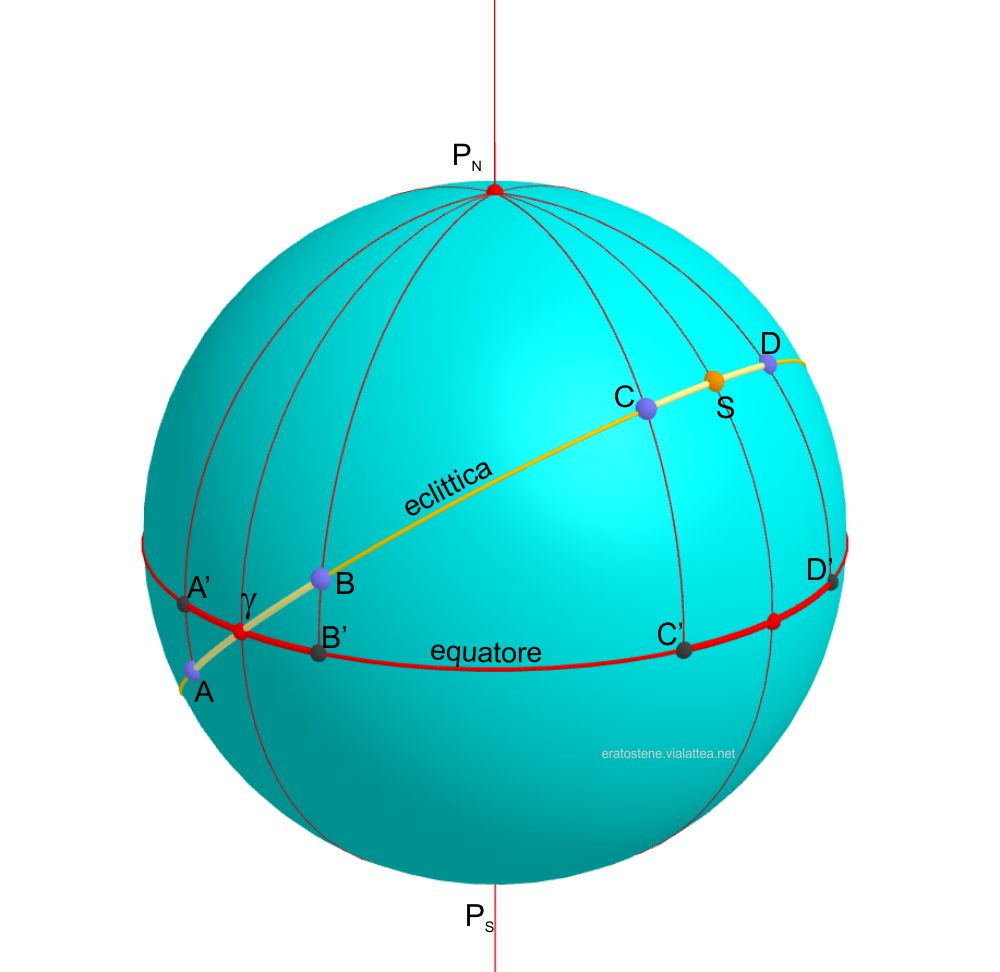
In questa immagine si esagera l’obliquità dell’eclittica cioè la sua inclinazione rispetto all’equatore celeste, allo scopo di evidenziare in modo intuitivo la differenza tra la lunghezza di archi di eclittica ($AB$ e $CD$) e le corrispondenti separazioni in ascensione retta ($A’B’$ e $C’D’$). L’eclittica e l’equatore si intersecano nei due nodi opposti: i punti equinoziali. Qui è rappresentato uno solo dei due nodi, il punto vernale ($\gamma$). Il punto $S$ rappresenta invece il punto solstiziale di giugno.
Il Sole, nel suo moto apparente annuo, percorre l’eclittica in senso antiorario se visto dal polo nord (moto diretto), aumentando la sua longitudine eclittica, cioè l’arco di eclittica che lo separa dal punto vernale. Di conseguenza aumenta anche la sua ascensione retta, cioè l’arco di equatore che lo separa dal punto vernale. Anche se il moto del Sole fosse uniforme lungo l’eclittica, il suo moto in ascensione retta non lo sarebbe comunque. La non uniformità della variazione di ascensione retta del Sole implica che l’intervallo del giorno solare vero non è costante e così la scala del tempo solare vero non è uniforme. Questo fatto geometrico legato all’obliquità dell’eclittica è una delle due cause della non uniformità del tempo solare vero.
Dall’immagine, si può intuitivamente dedurre che nei pressi dei punti equinoziali l’arco di equatore è minore del corrispondente arco di eclittica, mentre accade l’opposto nei pressi dei solstizi. Perciò il moto del Sole in ascensione retta rallenta attorno ai punti equinoziali ed accelera a cavallo dei punti solstiziali.
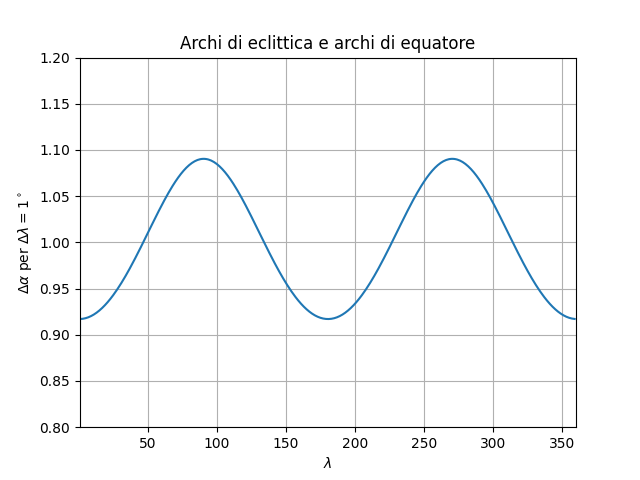
Questo grafico mostra come varia l’arco di equatore ($\Delta\alpha$) corrispondente ad un arco di eclittica di un grado, in funzione della longitudine eclittica ($\lambda$).
La variazione di ascensione retta minima è agli equinozi ($\lambda=0^\circ$ e $\lambda=180^\circ$) e vale circa $0^\circ\!,\!92$ per ogni variazione di $1^\circ$ di longitudine eclittica. La massima variazione è ai solstizi ($\lambda=90^\circ$ e $\lambda=270^\circ$) quando supera il grado: $\Delta\alpha=1^\circ\!,\!09$ per ogni grado di longitudine. Verso i $45^\circ$, i $135^\circ$, i $225^\circ$ e $315^\circ$ di longitudine le due variazioni si uguagliano.
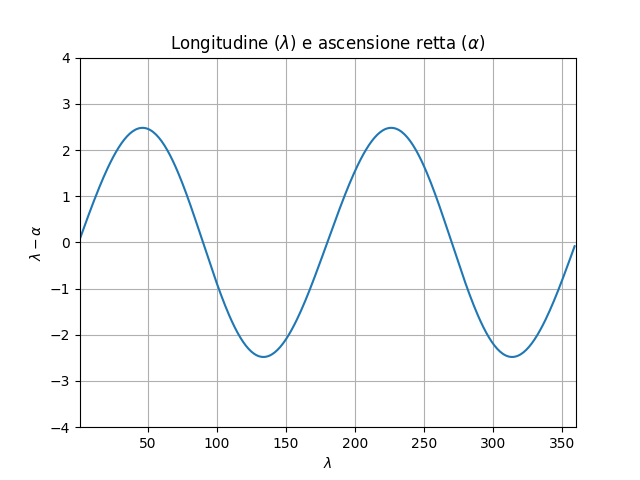
Qui è messo in grafico il “ritardo” dell’ascensione retta rispetto alla longitudine ($\lambda-\alpha$) sempre in funzione della posizione del Sole lungo l’eclittica.
Verso i $45^\circ$ e $225^\circ$ di longitudine si accumula il maggior ritardo mentre il maggior anticipo si raggiunge verso i $135^\circ$ e $315^\circ$. Longitudine e ascensione retta si uguagliano nei punti solstiziali e nei punti equinoziali.
Vedi anche: Equazione del tempo

