I cerchi verticali
Disegnare i cerchi verticali è la parte più complessa. La loro costruzione è più complicata e le regole di costruzione sono meno immediate da capire rispetto ai disegni fatti fino ad ora. Inoltre, per alcuni dei cerchi verticali si richiede un foglio di grandi dimensioni anche un grande compasso! Con un po’ di ingengno si può comunque risolvere. Ad esempio usando una tavola di legno sulla quale si possono piantare delle puntine e, al posto del compasso, una penna legata ad una cordicella. Si fissa una puntina nel centro del cerchio, si lega ad essa un’estremità della cordicella e all’altra estremità si lega la penna, nei pressi della punta. Il segno non sarà perfetto ma avrà una buona approssimazione rispetto alla traccia di un compasso.
Per capire come costruire i cerchi verticali basti pensare che essi passano tutti per lo zenit e per il nadir. L’asse zenit-nadir sulla proiezione stereografica coincide con il meridiano celeste. Dati i diversi azimut dei cerchi verticali, le loro proiezioni stereografiche avranno diverse dimensioni. Pur avendo diverse dimensioni, tutti questi cerchi devono comunque passare per lo zenit e il nadir. Così, lo zenit e il nadir nella proiezione stereografica diventano gli estremi di una corda comune a tutti i cerchi verticali. Ricordiamo una regola geometrica facilmente verificabile: l’asse di una corda di circonferenza passa sempre per il centro del cerchio. Una conseguenza di questa legge è che i centri di tutte le circonfereza che hanno in comune una stessa corda devono per forza trovarsi sull’asse della corda.
In base a queste considerazioni e sapendo che la proiezione stereografica conserva gli angoli alle intersezioni delle circonferenze e delle rette, possiamo trovare facilmente l’asse lungo il quale si dispongono i centri dei circoli verticali stereografici da disegnare.
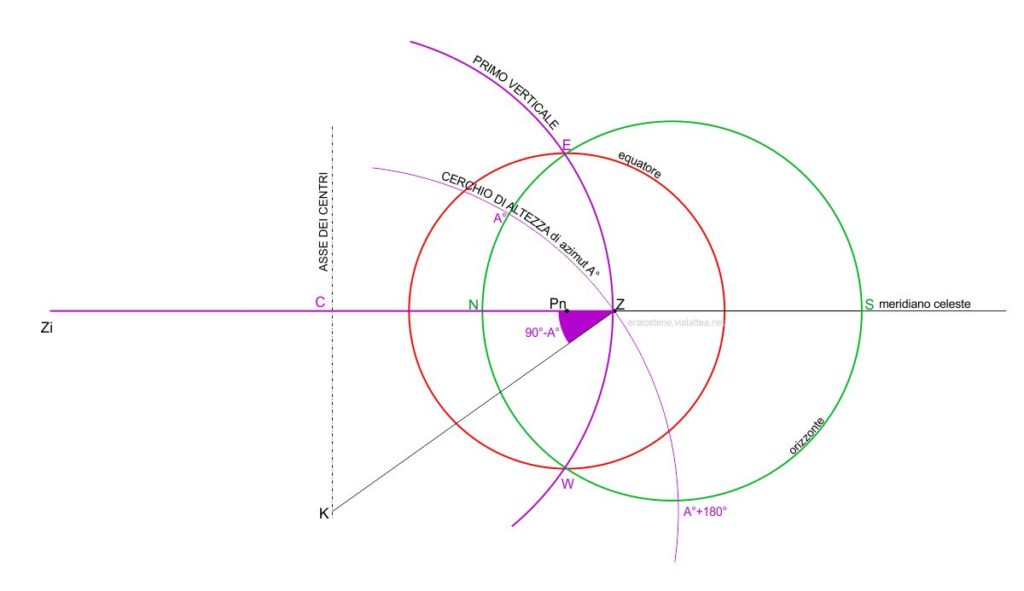
Consideriamo solo la proiezione stereografica, dato che quella ortografica non serve più per questa costruzione. Identifichiamo il punto medio $C$ del segmento $Z_iZ$ che congiunge il nadir con lo zenit.
Puntando il compasso in $C$ possiamo disegnare subito il primo verticale che è cerchio verticale notevole passante per i punti cardinali est e ovest. Osserviamo che esso forma angoli di $90^\circ$ gradi con l’orizzonte nei punti est e ovest. Tutti i cerchi verticali ,infatti, per definizione sono perpendicolari all’orizzonte. Il verticale nord, cioè quel cerchio verticale notevole che passa per il nord e il sud celesti coincide con il meridiano celeste e quindi è già stato disegnato.
Tracciamo ora l’asse del segmento $Z_iZ$, cioè quella retta che è perpendicolare ad esso e che passa per il suo punto medio $C$. Lo si può chiamare “asse dei centri” perché segneremo lungo questa retta tutti i centri dei cerchi verticali. Iniziamo con il tracciare un cerchio verticale che interseca l’orizzonte di nord-est in un punto di azimut $A^\circ$. Esso inncontretà l’orizzonte anche sul versante opposto di sud-ovest nel punto di azimut $A^\circ+180$. Per trovare il centro di questo cerchio verticale pensiamo che esso è ruotato di $90^\circ-A^\circ$ verso ovest rispetto al verticale nord. Così, dato che sulla proiezione stereografica si mantengono gli angoli, possiamo tracciare il suo raggio $ZK$ ruotato di $90^\circ-A°$ in senso antiorario rispetto al meridiano. Il punto $K$ identificato in questo modo è il centro dove puntare il compasso. Osserviamo che, se il disegno è corretto, il cerchio verticale deve formare $90^\circ$ con l’orizzonte nei punti di intersezione.
Dal punto di vista matematico, abbiamo già visto come si calcolano le distanze $ZP_N$ e $Z_iP_N$. Esse dipendono dalla latitudine $\varphi$ e dal raggio $R$ dell’equatore. Così, anche distanza $CP_N$ dell’asse dei centri dal centro $P_N$ dell’astrolabio e il raggio $CZ$ del primo verticale dipendono, alla fine, solo da $\varphi$ e da $R$. Noti $ZP_N$ e $Z_iP_N$, essi si calcolano così:
$$CZ=\frac{Z_iP_N+ZP_N}{2}$$
$$CP_N=CZ-ZP_N$$
La distanza dal meridiano celeste del centro di un cerchio verticale che inizia ad oriente in un punto$K$ di azimut $A^\circ$, cioè la lunghezza del segmento $KC$ si calcola ora facilmente, noto il raggio $CZ$:
$$CK=CZ\tan{(90^\circ-A^\circ)}$$
Qui è interessante poter calcolare in anticipo la distanza $KZ$ che è il raggio di un cerchio verticale di azimut $A^\circ$:
$$KZ=\frac{CK}{\cos{A^\circ}}$$
Infatti, i raggi $KZ$ dei circoli verticali prossimi al meridiano celeste sono molto grandi. Ad esempio, utilizzando i valori che abbiamo già usato di $R10 cm$ e $\varphi=40^\circ$, la distanza $CK$ risulta di $74 cm$ e il raggio $KZ$ del cerchio orario dei $10^\circ$ di azimut è $75 cm$!
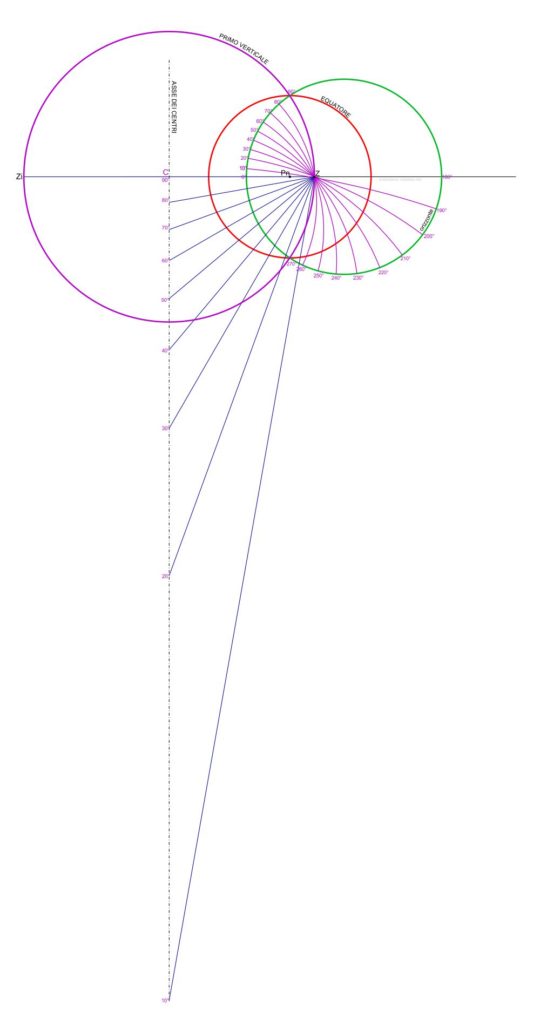
Ecco come si presenta la costruzione dei primi $8$ circoli orari distanti $10^\circ$ l’uno dall’altro. I restanti $8$ sono simmetrici a questi e si costruiscono in modo simmetrico rispetto al meridiano celeste.
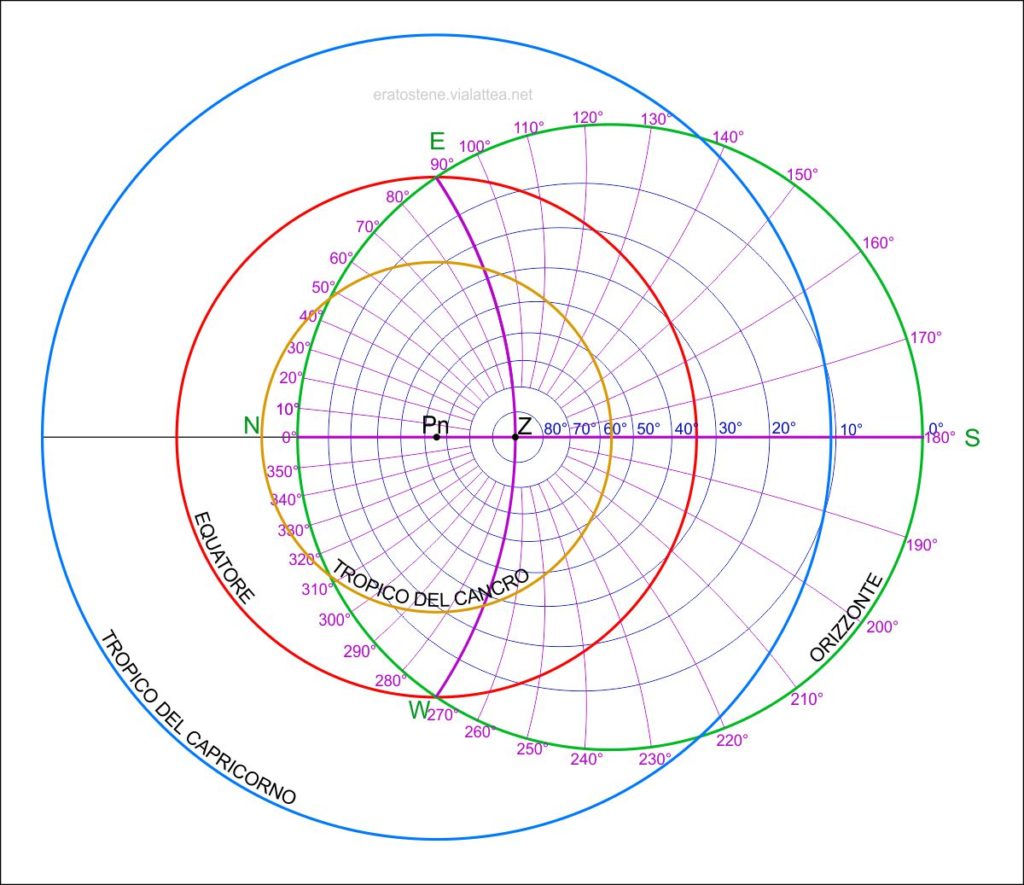
Ecco come si presenta la rete altazimutale completa, con $16$ cerchi verticali e $8$ almucantarat, rispetto all’equatore e ai due tropici.
Si noterà la disposizione dei punti cardinali est e ovest rispetto al nord e al sud: chi ha prestato attenzione alle considerazioni fatte, avrà capito che la sfera celeste che stiamo disegnando è vista dal di fuori. Immaginiamo di sollevarci al di sopra del polo nord celeste, “uscire” dalla sfera celeste, e guardarla in questo modo. Così, la ghiera graduata dell’azimut cresce da nord in senso orario. Allo stesso modo si rappresenteranno le stelle sulla rete: la loro posizione sarà individuata in base alle loro coordinate equatoriali. L’ascensione retta dovrà essere letta su una scala che cresce in senso antiorario partendo dalla direzione del punto vernale.
A questo punto del nostro lavoro si può decidere se costruire un astrolabio che rappresenti la sfera celeste “vista da fuori” oppure “vista da dentro”. Come abbiamo già detto nell’introduzione, il nostro esempio è del primo tipo. Se si decide per il secondo tipo si dovrà invertire il senso della scala di azimut e quindi scambiare tra loro le posizioni dei punti cardinali est e ovest. Anche nelle prossime pagine si dovrà prestare attenzione alle scale di ascensione retta e al circolo delle date: entrambe dovranno essere invertite di senso. Tutto il resto rimane identico.
Costruiamo ora la scala stereografica.

