L’astrolabio moderno: il circolo delle date
A questo punto del lavoro possiamo concludere con il disegno sulla rete di un circolo delle date, di $365$ giorni, associato alla scala dell’ascensione retta in modo tale da mettere nella giusta relazione il tempo siderale con il calendario. Il circolo delle date appare negli astrolabi moderni mentre, in quelli tradizionali, esso era disegnato sul dorso e, associato ad un circolo solare, permetteva di calcolare la longitudine eclittica del Sole per ogni data (vedi ad esempio l’equatorium solare).
La presenza del circolo delle date sulla rete degli astrolabi moderni permette invece un rapido calcolo analogico del tempo siderale in base al tempo solare medio e fornisce la posizione delle stelle rispetto all’orizzonte dell’osservatore. La costruzione della scala delle date, pur non essendo facilissima, e la sua sistemazione in relazione alla scala di ascensione retta fornisce lo spunto per interessanti considerazioni.
L’anno tropico è un intervallo di tempo di $365$ giorni e $\frac{1}{4}$ ($\text{365,2422}$ giorni SI). Il nostro calendario contiene invece un valore intero di $365$ o $366$ giorni e per costruire l’astrolabio siamo costretti ad accettare come approssimazione una suddivisione di $365$ giorni.
Il primo problema è prettamente grafico e consiste nel suddividere l’angolo giro di $360^\circ$ in $365$ parti uguali. Ne risulta che le tacche dei giorni devono essere distanziate di $360^\circ:365 = \text{0,9863}^\circ$. Per chi sa utilizzare un programma di grafica vettoriale il problema è facilmente risolvibile. Nel caso di un disegno a mano, si può scegliere di indicare soltanto le tacche delle date 1, 5, 10, 15, 20 e 25 di ogni mese. La distanza angolare tra due tacche qualsiasi si ottiene moltiplicando il numero di giorni che le separano per $\text{0,9863}^\circ$ e poi approssimando graficamente.
Il secondo problema è quello di far coincidere ogni data con il tempo siderale corretto. Esistono varie modalità di corrispondenza tra la scala del calendario e la scala di ascensione retta per trasformare l’astrolabio in un calcolatore analogico del tempo siderale. Da questa scelta dipenderà il modo di lettura e di utilizzo dell’astrolabio. Io propongo di usare il seguente riferimento: alla mezzanotte UT del 20 settembre, cioè alle $0^h$ UT del 21 settembre, il tempo siderale medio a Greenwich $(GMST^{0\,UT})$ è molto vicino a $0^\circ$.
Una tabella di valori di $GMST$ alle ore $0$ UT del 21 settembre di cinque anni successivi di cui il primo e l’ultimo sono bisestili è utile per capire come varia il tempo siderale con il succedersi di intervalli di un anno di calendario (valori calcolati per mezzo del software Skyfield) :
2016: $00^h01^m\text{12,2}^s$
2017: $00^h00^m\text{15,5}^s$
2018: $23^h59^m\text{17,9}^s$
2019: $23^h58^m\text{20,4}^s$
2020: $00^h01^m\text{19,7}^s$
Il primo valore ci dice che alla mezzanotte del 20 settembre 2016 il punto gamma ha già passato il meridiano da $1^m12^s$. Invece, dopo 365 giorni civili, alla mezzanotte del 20 settembre 2027, il punto gamma ha passato il meridiano da soli $16^s$ e cioè con un ritardo di $57^s$ rispetto all’anno precedente. Lo stesso ritardo di $57^s$ si accumula negli anni successivi tanto che nel 2019 il punto gamma passerà al meridiano circa un minuto e $40$ secondi dopo la mezzanotte.
Questo ritardo di $57^s$ si spiega dal fatto che l’anno tropico dura $\text{365,2422}$ giorni mentre il nostro controllo è fatto dopo un intervallo di soli 365 giorni. Perciò mancano $\text{0,2422}$ giorni al completamento dell’anno tropico. Il Sole medio percorre l’equatore alla velocità di $360^\circ/\text{365,2422}^d=\text{0,9865}^\circ$ e, dopo $365$ giorni, gli mancano da percorrere $\text{0,9865}^\circ\times\text{0,2422}=\text{0,2387}^\circ=\text{57,3}^s$. Questa diffenza di ascensione retta del Sole a distanza di un anno $(\alpha_2-\alpha_1)$ è uguale alla differenza di tempo siderale $(\theta_2-\theta _1)$. Infatti, dalla relazione fondamentale (vedi Tempo e ascensione retta):
$$\theta = t + \alpha$$
dove $t$ è l’angolo orario del Sole medio, si ricava:
$\theta_2-\theta_1=(t_2+\alpha_2)-(t_1+\alpha_1)$
A mezzanotte UT, l’angolo orario del Sole medio è, in entrambi i casi:
$t_1=t_2=12^h$
perciò, in conclusione:
$$\theta_2-\theta _1=\alpha_2-\alpha_1$$
La differenza di ascensione retta del Sole medio giustifica le differenze di tempo siderale tra gli anni 2016, 2017, 2018 e 2019.
Per la mezzanotte UT del 20 settembre 2020, con l’inserimento del giorno intercalare, sono passati 366 giorni e ci si dovrebbe aspettare un ritorno del tempo siderale al valore del 20 settembre 2016. C’è invece una differenza di circa $7,5$ secondi.
Ciò dipende ancora dal calendario. Quattro anni di calendario gregoriano contengono $365\times4+1$ giorni, cioè $\text{365,25}\times4$, mentre quattro anni tropici contengono $\text{365,2422}\times4$ giorni. C’è una differenza di:
$(\text{365,25}-\text{365,2422})\times4=\text{0,0312}$ giorni
Il Sole medio, in questa frazione di tempo percorre:
$\text{0,0312}\times\text{0,9865}^\circ=\text{0,0308}^\circ$ sull’equatore
che equivalgono a quei $\text{7,5}^s$ di differenza quadriennale di tempo siderale. Questa differenza quadriennale, che vale in media $8$ secondi, non viene corretta dai giorni intercalari degli anni bisestili ma si accumula in $100$ anni. Viene parzialmente corretta dal sistema del calendario gregoriano saltando 3 bisestili ogni 4 anni secolari.
La corrispondenza delle date con l’ascensione retta diventa uno strumento di calcolo dell’ora siderale per qualsiasi località a qualsiasi ora. Infatti, a cavallo della mezzanotte UT del 20 settembre, il tempo siderale locale sarà all’incirca uguale a zero non solo al meridiano fondamentale ma anche in qualsiasi altro luogo sulla Terra, alla mezzanotte di tempo medio locale. Per le località poste esattamente sul meridiano centrale di un fuso lo zero siderale corrisponderà alla mezzanotte civile di quel fuso (escludendo eventuali correzioni dovute all’ora legale estiva). Ovviamente ci sarà sempre una minima differenza rispetto allo zero siderale che dipende dalla differenza tra il tempo medio locale e la mezzanotte UT. L’errore massimo è comunque accettabile per l’uso che facciamo del nostro strumento: sono dieci secondi all’ora che si accumulano fino ad un massimo di $\pm2^m$ su $\pm12^h$ di differenza. Molto più importante è invece l’errore che si può produrre se si regola la data sul tempo civile del fuso e non sul tempo medio locale: sono 4 minuti di differenza per ogni grado di longitudine che separa il luogo di osservazione dal meridiano centraile del fuso (vedi Il tempo e le differenze di longitudine e Tempo meccanico e tempo degli orologi solari).
Vedremo come calcolare il tempo siderale locale nel miglior modo possibile quando discuteremo sull’uso dell’astrolabio.
In pratica, per disegnare il circolo delle date, assumiamo che ogni tacca dei giorni corrisponda alle ore $0^h$ della data da esse indicata e iniziamo la costruzione della scala facendo corrispondere la tacca del 21 settembre con quella dei $180^\circ$ di ascensione retta.
- si numerano da 0 a 366 i giorni di un anno non bisestile cominciando dal 21 di settembre in corrispondenza dei $180^\circ$. In questo modo, il 21 settembre è il giorno n.0, il 25 di settembre è il n.4, il primo novembre è il n.41, e così via.
- Se $n$ è l’ennesimo giorno da rappresentare a fianco della scala dell’ascensione retta, la sua tacca si disegnerà in corrispondenza di $n\times\text{0,9863}^\circ$ in senso antiorario rispetto al punto di partenza del 21 settembre, cioè in corrispondenza del valore di ascensione retta $n\times\text{0,9863}^\circ+180^\circ$. Una tabella con questi calcoli già predisposti può essere di aiuto.
La corrispondenza tra le ore zero del 21 settembre e i $180^\circ$ di ascensione retta predispone un metodo di lettura dell’ora siderale che possiamo verificare facilmente dopo aver sovrapposto la rete alla lamina:
- facciamo coincidere la tacca del 21 settembre (cioè la mezzanotte del 20 settembre) sulle ore 24 della scala oraria della lamina vedremo che il punto vernale $\gamma$ si troverà sul meridiano celeste superiore (esattamente a sud) segnando le zero ore siderali, come ci si doveva aspettare. Il giorno successivo, mettendo la tacca del 22 settembre sempre sulle ore 24, sarà passato un giorno solare medio ma non ancora un giorno siderale e al punto gamma mancheranno poco meno di 4 minuti per giungere al meridiano (il giorno siderale dura $23^h56^m$).
- Ponendo una data qualsiasi in corrispondenza di un istante della scala oraria si otterrà una buona approssimazione della posizione del punto gamma rispetto al meridiano in quell’istante di tempo medio (vedi un simulatore).
Nelle prossime pagine si descriveranno le correzioni da apportare per una lettura più precisa del tempo siderale.
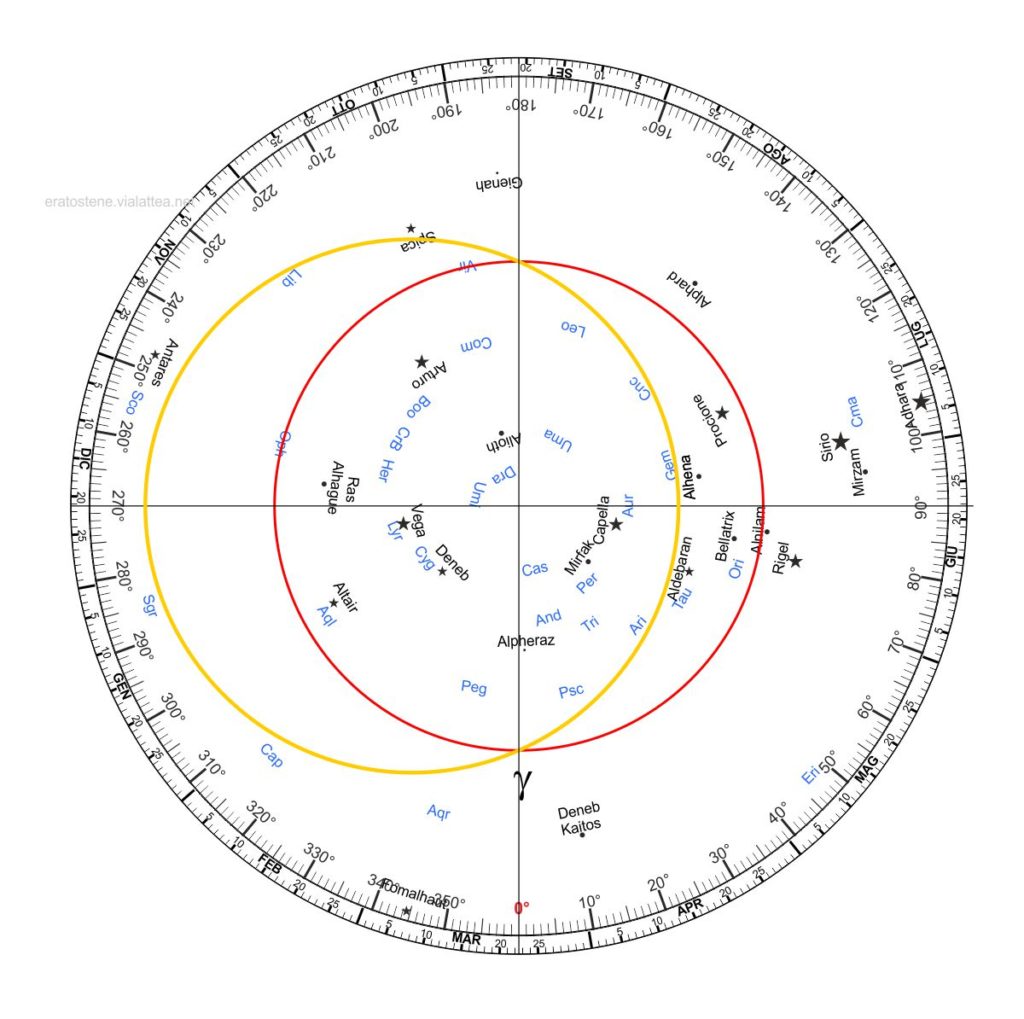
La rete ora è completa con il circolo delle date. Il suo bordo esterno deve cincidere con il bordo interno del circolo delle ore disegnato sulla lamina.
Nella prossima pagina vedremo l’aspetto definitivo dell’astrolabio moderno montato.

