Il circolo menaeus
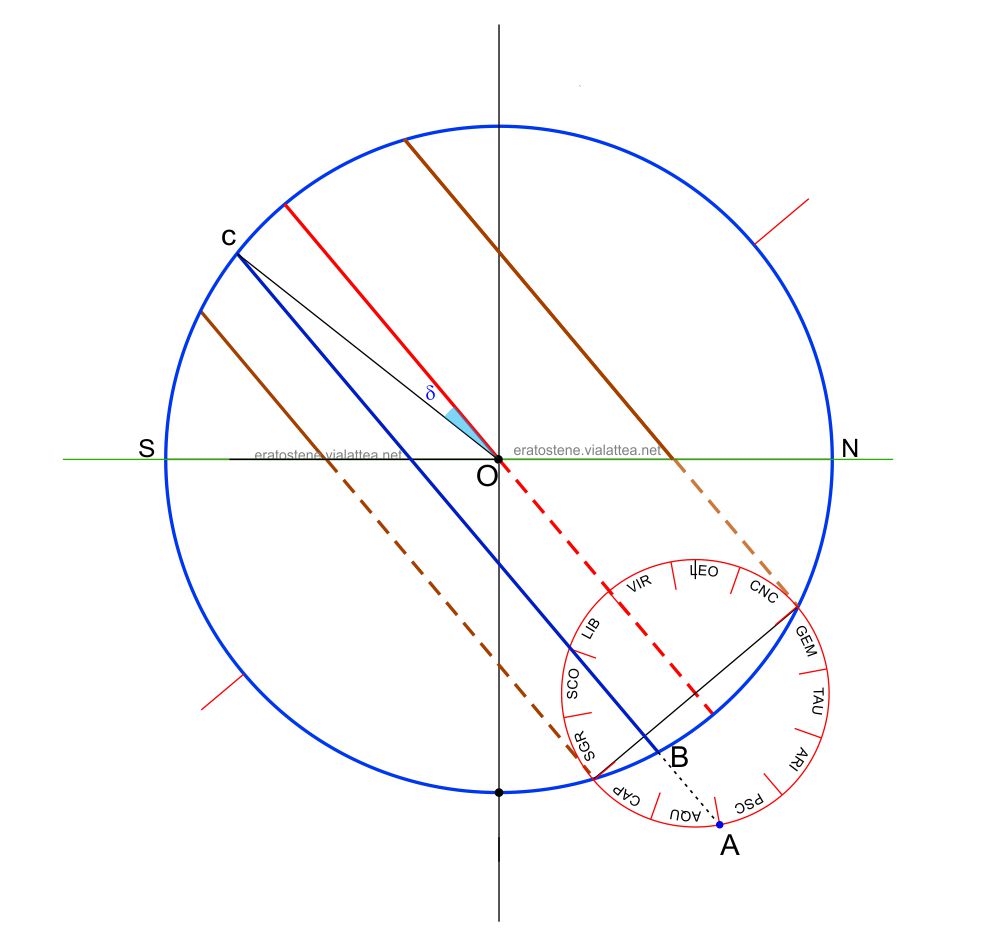
Il menaeus (trascrizione dal greco μηναῖος, un aggettivo che significa “mensile”, “riguardante i mesi”) è l’ultimo dettaglio dell’analemma di Vitruvio che descriviamo qui, ma non è il meno interessante. Potremmo definire il circolo menaeus come una “macchina nella macchina”. Esso ci permette di trovare graficamente il parallelo di declinazione che corrisponde ad una determinata longitudine eclittica del Sole. Rimando alla pagina sullo zodiaco per quanto riguarda la relazione tra la longitudine e le case dello zodiaco. Basti sapere che la longitudine eclittica, che attualmente si misura da $0^\circ$ a $360^\circ$ in senso antiorario a partire dal punto vernale, anticamente era misurata come posizione all’interno di una delle case di $30^\circ$ ciascuna in cui era divisa l’eclittica.
Il circolo va disegnato con il suo diametro posto tra i punti di intersezione dei due paralleli solstiziali con il circolo meridiano. Il primo punto della casa del Cancro è all’intersezione del parallelo del solstizio di giugno. Seguono gli altri segni in senso antiorario.
Ad esempio, se dobbiamo trovare il parallelo di declinazione corrispondente al primo punto dei Pesci, si segna il punto $A$ (corrispondente alla longitudine eclittica di $330^\circ$), poi si traccia una parallela all’equatore che passa per $A$. Le sue intersezioni $B$ e $C$ con il meridiano celeste sono gli estremi del segmento che rappresenta il parallelo di declinazione $\delta$ cercato.
In conclusione, se desideriamo arricchire il quadrante del nostro orologio solare aggiungendo le linee diurne di alcune date dell’anno, oltre a quelle degli equinizi e dei solstizi, possiamo consultare una tabella delle longitudini eclittiche per quelle date e ricavare i corrispondenti paralleli di declinazione usando il menaeus.
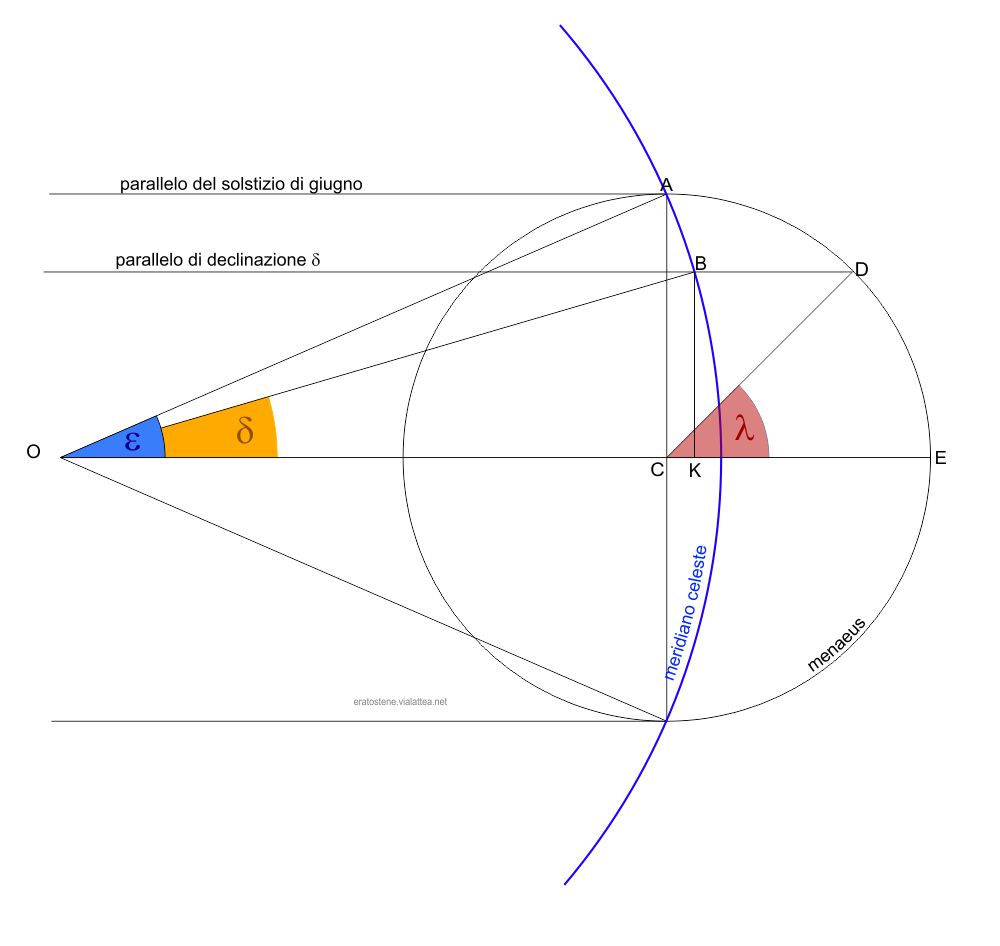
Per chi è più curioso, spiegiamo qui il significato matematico del menaeus. Esso è un calcolatore analogico della funzione che restituisce la declinazione $\delta$ di un punto dell’eclittica in base alla sua longitudine:
$\boxed{\sin\delta=\sin\lambda\cdot\sin\epsilon}$
dove $\lambda$ è la longitudine di un punto dell’eclittica e $\epsilon$ è l’obliquità dell’eclittica, attualmente uguale a circa $23^\circ\!,\!5$ (per il significato di questa formula vedi anche qui).
Dimostriamolo assumendo che l’analemma sia un cerchio trigonometrico di raggio unitario ($OA=1$). Ne deriva che il raggio del menaeus è:
$AC=\sin\epsilon$
Ricaviamo ora il segmento $BK$ sia in base al cerchio dell’analemma che in base al menaeus:
$BK=\sin\delta$
e
$BK=AC\cdot\sin\lambda=\sin\epsilon\cdot\sin\lambda$
perciò:
$\sin\delta=\sin\lambda\cdot\sin\epsilon$

