L’ora solare
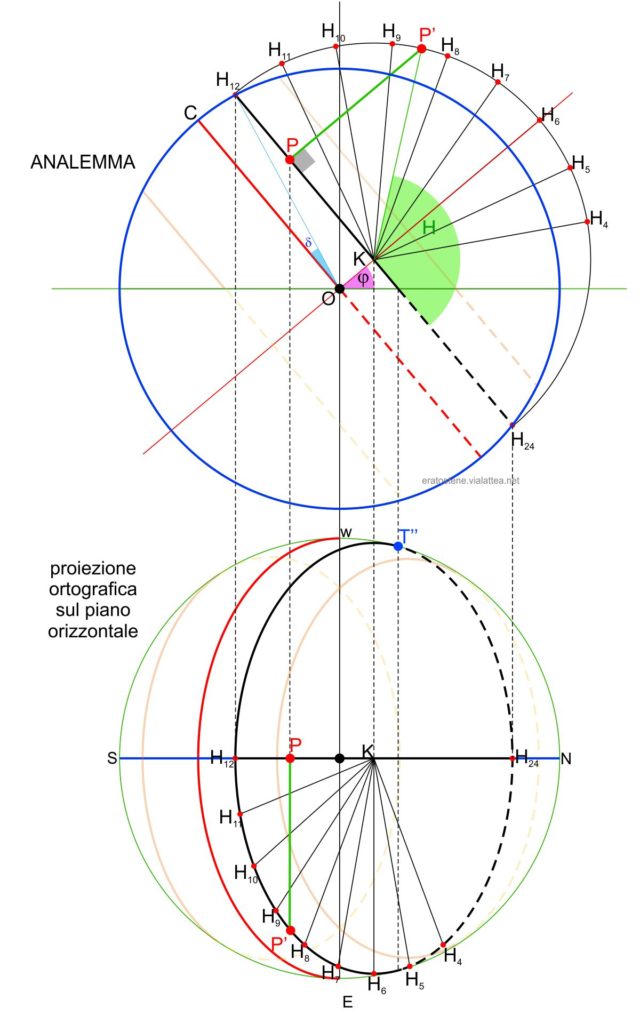
Tracciano una perpendicolare per $P$ si interseca la semicirconferenza ribaltata nel punto $P’$. La lunghezza del segmento $PP’$ disegnato in questo modo si conserva anche nella proiezione ortografica orizzontale dove lo vediamo rappresentato. Infatti l’ellisse è il cerchio del parallelo di declinazione “schiacciato” lateralmente in direzione nord-sud, perciò tutte le lunghezze verticali si conservano. Quest’ultima osservazione serve solo a capire che non stiamo sbagliando se misuriamo l’angolo $P’\hat{K}H_{24}$ per trovare l’ora solare $H$, cioè l’angolo orario del Sole, tipicamente misurato a partire dalla mezzanotte.
Già ora possiamo capire l’importanza dell’analemma di Vitruvio nel rappresentare la sfera celeste: senza dover ricorrere a curve complesse come l’ellisse, ma semplicemente usando compasso e squadra, dalla semplice proiezione $P$ della posizione di un astro sulla superficie della sfera celeste si possono ricavare quattro sue coordinate l’altezza, l’azimut, la declinazione e l’angolo orario: le due coordinate altazimutali e le due coordiane del sistema orario.
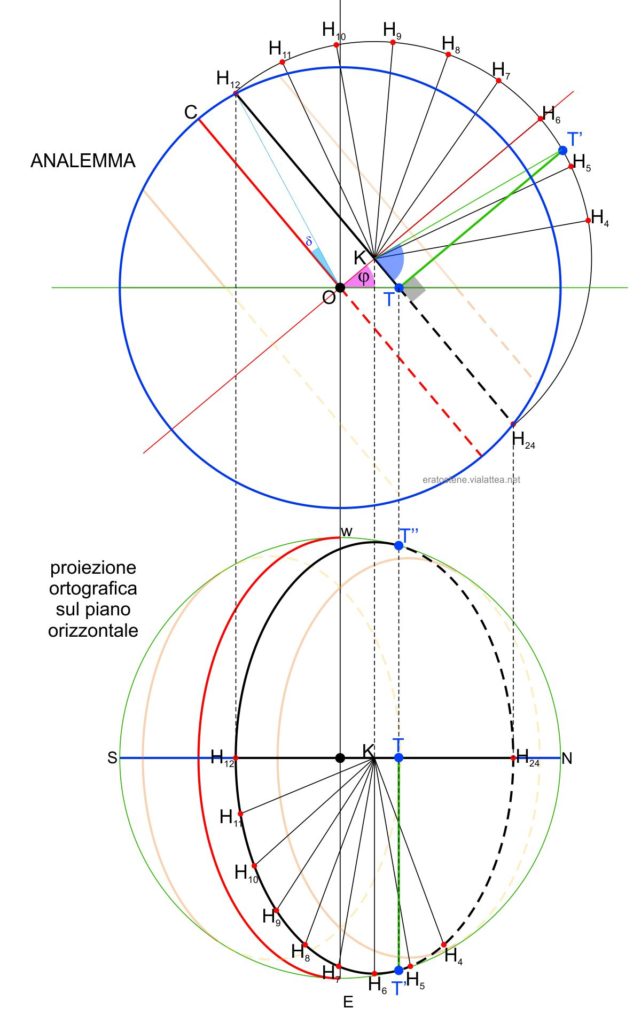
Con lo stesso metodo troviamo anche l’ora del sorgere del Sole quando la sua declinazioe è $\delta$. Quando il Sole sorge si trova all’orizzonte, quindi nel punto $T$ di intersezione tra il suo parallelo di declinazione e la linea dell’orizzonte dell’analemma. Tracciando la perpendicolare $TT’$ come abbiamo fatto prima per il punto $P$, si forma l’angolo $H_{24}\hat{K}T’$ che rappresenta l’ora del sorgere. In questo modo possiamo limitare il numero di linee orarie da calcolare in base all’ora del sorgere del Sole per una certa data e una certa latitudine.
Questa operazione che abbiamo fatto per le ore mattutine si ripete simmetricamente per le ore pomeridiane per cui ad esempio il punto $H_{11}$ troverà il suo simmetrico nel punto $H_{13}$, il punto $H_{10}$ nel simmetrico $H_{14}$, e così via.
Riconsiderando ad esempio il punto $P$, se l’ora mattutina è, come abbiamo detto, definita dall’angolo $P’\hat{K}H_{24}$ (all’incirca le ore $8:30$) la corrispondente ora solare pomeridiana si troverà misurando l’angolo $H_{12}\hat{K}P’$ (all’incirca le $3:30$ del pomeriggio). I due angoli sono supplementari.
Troviamo così che l’alba avviene tra le $5$ e le $6$ del mattino, mentre il tramonto (quando il Sole si trova nel punto simmetrico $T”$) avviene tra le $6$ e le $7$ pomeridiane. L’angolo da misurare per il tramonto è $H_{12}\hat{K}T’$.

