Come ricavare l’altezza e l’azimut di un punto dalla sua proiezione
Uno degli aspetti interessanti dell’analemma è la possibilità di trovare graficamente l’altezza e l’azimut di un punto sulla sfera partendo dalla sua proiezione ortografica.
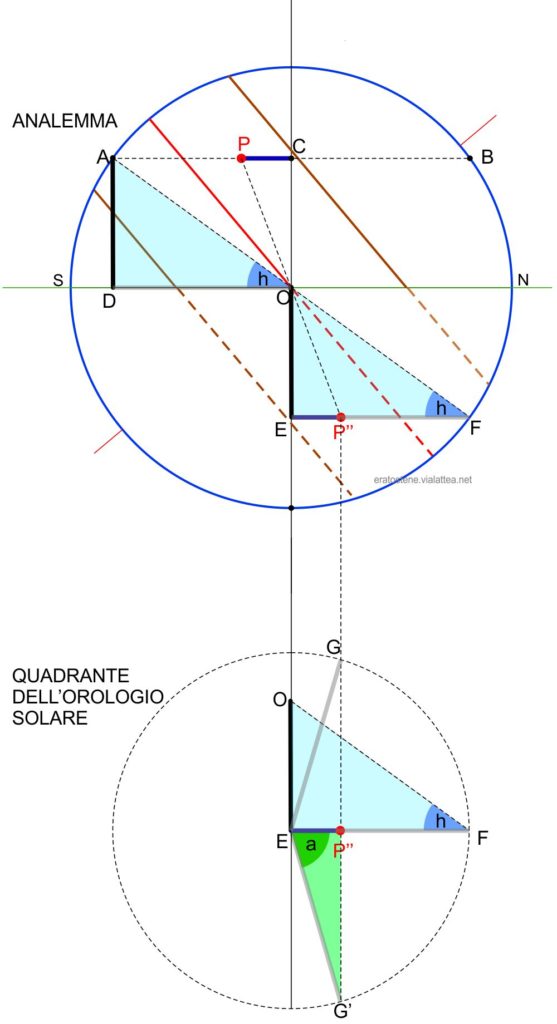
Visto che l’interesse principale dell’analemma è rivolto alla posizione del Sole, e alla possibilità di simulare la proiezione della sua ombra sulla superficie di un quadrante solare, prendiamo come esempio il punto $P$ che potrebbe rappresentare il Sole ad una qualsiasi ora e una qualsiasi data. Il punto $P$ infatti è compreso tra i due paralleli di massima e minima declinazione. Sulla reale posizione del Sole rappresentato da $P$ rimane una sola incertezza. Quando guardiamo questa proiezione meridiana, infatti, dobbiamo sempre immaginare che il nostro punto di osservazione si trova al di fuori della sfera celeste, lungo la direzione cardinale est. Il punto $O$ al centro del cerchio meridiano rappresenta sia il punto cardinale est (che si trova nell’emisfero orientale, al di sopra del foglio) che il punto cardinale ovest (che si trova nell’emisfero occidentale, al di sotto). Se la posizione del Sole è proiettata in $P$ sul piano meridiano, significa che l’astro potrebbe trovarsi nell’emisfero orientale (prima del mezzogiorno) oppure in quello occidentale (dopo il mezzogiorno). Le due posizioni sono simmetriche rispetto al piano meridiano. In entrambi i casi il Sole avrebbe la stessa altezza rispetto all’orizzonte ma due diversi azimut.
Dopo queste premesse, tracciamo un segmento $AB$ che passa per $P$, parallelo all’orizzonte. Tale segmento rappresenta il parallelo di altezza che passa per $P$ (o almucantarat di $P$), cioè il circolo parallelo all’orizzonte composto da tutti i punti che hanno la stessa altezza di $P$. Di conseguenza, possiamo tracciare tre segmenti, $AO$, $DO$ e $DA$ che formano un triangolo rettangolo retto in $D$ il quale simula uno gnomone verticale ($AD$) e la sua ombra ($DO$). Il Sole, infatti, produrrebbe sempre ombre di uguale lunghezza anche se si trovasse in qualsiasi altro punto dello stesso almucantarat. Questa simulazione ci permette di misurare graficamente (o calcolare) l’altezza del Sole, cioè l’angolo $D\hat{O}A=h$ data una posizione $P$.
Se la distanza del punto $P$ dal piano orizzontale (cioè il segmneto $AD$) ci offre la misura dell’altezza, la sua distanza dalla verticale (segmeno $PC$) ci offrirà un modo per trovare l’altra coordinata, l’azimut. Quest’ultima rappresenta la distanza del Sole dal piano verticale est-ovest.
Per capire, eseguiamo due traslazioni del triangolo $ADO$. La prima, lungo la direzione $AO$, porta il triangolo a nord della linea est-ovest nella nuova posizione $OEF$. Questa operazione ha due vantaggi. Il primo è che possiamo riportare facilmente la distanza $PC$ sul segmento $EP”$, semplicemente tracciando una retta che passa per $P$ e per il centro $O$. Il secondo vantaggio è che questa posizione ci suggerisce meglio la situazione che stiamo studiano: il Sole si trova a sud della linea est-ovest e quindi la sua ombra si proietta a nord della stessa. Ci rimane da capire in quale direzione è proiettata l’ombra per misurare l’azimut. Per fare questo procediamo con una seconda traslazione, questa volta in verticale scegliendo una distanza a piacere dal centro dell’analemma. Questa seconda traslazione ha come unico scopo quello di non sovrapporre troppi segni e di preparare il disegno del quadrante della meridiana su uno spazio libero del foglio.
Guardando il nuovo disegno, immaginiamo adesso di “raddrizzare” il triangolo $OEF$ ruotandolo rispetto alla direzione dell’ombra $EF$. Così, lo gnomone si trova nel punto $E$ e dobbiamo immaginarlo perpendicolare al foglio, con l’estremità rivolta verso di noi. Il piano del foglio diventa così il quadrante orizzontale dell’orologio solare sul quale disegnare le linee orarie. Dato che il segmento $PC$, come abbiamo detto, rappresenta la distanza del Sole dal piano verticale est-ovest, il segmento $EP”$ uguale ad esso, rappresenta la distanza dell’estremità dell’ombra dalla linea est-ovest. Qualsiasi punto della retta verticale che passa per $P”$ potrebbe rappresentare la posizione di questa estremità sul piano orizzontale. In realtà solo due punti sono possibili: quelli che rispettano la giusta lunghezza dell’ombra, cioè la lunghezza del segmento $EF$. Per trovarli si traccia una circonferenza puntando il compasso in $E$ e con apertura $EF$. Le due intersezioni $G$ e $G’$ tra questa circonferenza e la verticale che passa per $P”$ rappresentano le due possibioli posizioni dell’estremità dell’ombra. In particolare, $G$ rappresenta la posizione al mattino, quando il Sole si trova nell’emisfero orientale, mentre il punto $G”$ è la posizione pomeridiana, quando il Sole è nell’emisfero occidentale.
L’azimut $a$ dell’ombra pomeridiana è l’angolo $F\hat{E}G’$. L’azimut del Sole si ottiene aggiungendo $180^\circ$ a questo valore. Con una serie di aggiustamenti per la scelta del quadrante corretto si può misurare (o calcolare) sia l’azimut del Sole che quello della sua ombra.
Se lo scopo è solo quello di calcolare altezza e azimut, questa costruzione ci basterebbe. In realtà, l’analemma è una macchina grafica che deve servire per disegnare effettivamente il quadrante di un orologio solare. Ci accorgiamo perciò di un difetto fondamentale di questa costruzione per lo scopo pratico: l’altezza dello gnomone, cioè il segmento $AD$ varia al variare della distanza di $P$ dal piano dell’orizzonte. Noi invece abbiamo bisogno di uno gnomone di lunghezza fissa in base al quale poter disegnare il quadrante. Nella prossima pagina si risolverà questo problema.

