Linea diurna del solstizio di giugno
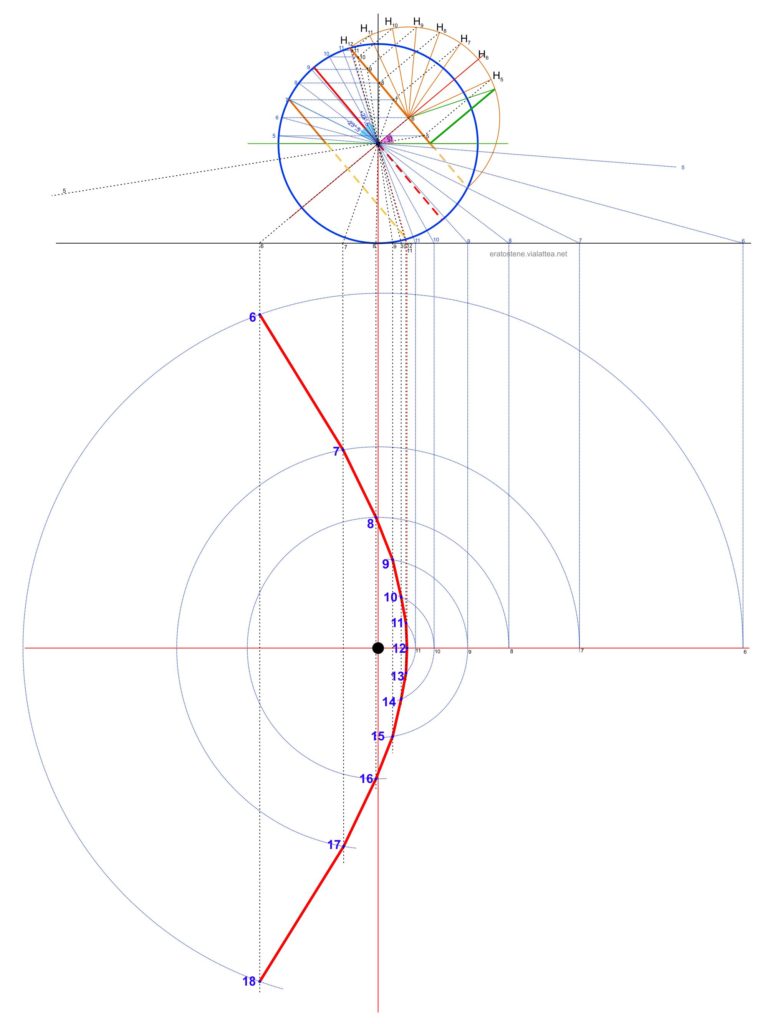
Possiamo passare alla costruzione di un quadrante orizzontale. Iniziamo considerando il parallelo di declinazione $\delta=+23^\circ\!,\!5$.
Una volta individuate l’ora dell’alba e l’ora del tramonto per la latitudine $\varphi$ scelta, applichiamo il procedimento descritto nelle pagine precedenti e lo ripediamo per le ore utili (in questo caso dalle ore $5$ alle ore $12$). Il disegno sembra molto complesso ma non è difficile trovare il percorso di costruzione che inizia con una certa ora segnata sul circolo del parallelo, ad esempio dal punto $H_8$, e seguire le linea tratteggiata che parte da esso, inconta perpendicolarmente il segmento del parallelo di declinazione nel punto $8$ e da lì si biforca (seguire sempre il n.$8$…) con due segmenti tratteggiati, uno per costruire la lunghezza dell’ombra dello gnomone e l’altro per trovare i punti di azimut.
Osserviamo che le ore prossime all’alba e al tramonto, come ad esempio le ore $5$ e le ore $6$ corrispondenti alle simmetriche pomeridiane delle ore $19$ e delle ore $18$, richiedono un foglio molto grande per l’individiazione delle estremità dell’ombra. Nel nostro caso le estremità per le ore $5$ e $19$ non sono nemmeno rintracciabili se non raddoppiando in larghezza il foglio.
Congiungendo tutti i punti trovati per le varie ore si ottiene una spezzata che rappresenta la curva del percorso dell’estremità dello gnomone durante il giorno. Questa curva è chiamata linea diurna. Ogni giorno dell’anno ha la sua linea diurna. Questa che abbiamo appena disegnato è la linea diurna del solstizio di giugno.

