Perché funziona?
La meridiana analemmatica utilizza la variazione di azimut del Sole nel corso della giornata (è una meridiana azimutale). Le meridiane azimutali offrono la lettura diretta dell’azimut per mezzo di uno stilo verticale (vedi anche: misurare l’azimut del Sole). L’azimut del Sole di un certo istante dipende geometricamente e matematicamente da tre parametri: la latitudine dell’osservatore, la declinazione e l’angolo orario del Sole di quell’istante. Perciò, conoscendo azimut, latitudine e declinazione si determina necessariamente l’ora. I quadranti delle meridiane azimutali a stilo fisso possiedono numerose curve di data (o scale giornaliere) che sono le proiezioni sul piano di paralleli di declinazione; esse si intersecano con curve orarie che invece rappresentano proiezioni di cerchi orari. La lunghezza dell’ombra dello stilo non ha alcuna importanza nella lettura. L’intersezione tra l’ombra e una certa linea della scala giornaliera, interseca anche una certa curva oraria che indica l’ora. Nel caso particolare dell’orologio analemmatico, uno speciale procedimento geometrico proiettivo fa in modo che tutte le linee di data coincidano in un’unica linea (l’ellisse) e che tutte le linee orarie diventino punti orari sull’ellisse. Questa notevole semplificazione si ottiene a patto di poter spostare lo stilo verticale lungo la linea meridiana, in un punto diverso per ogni data.
Mi ripropongo qui di spiegare nel modo più semplice possibile le ragioni delle formule usate per la costruzione della meridiana analemmatica.
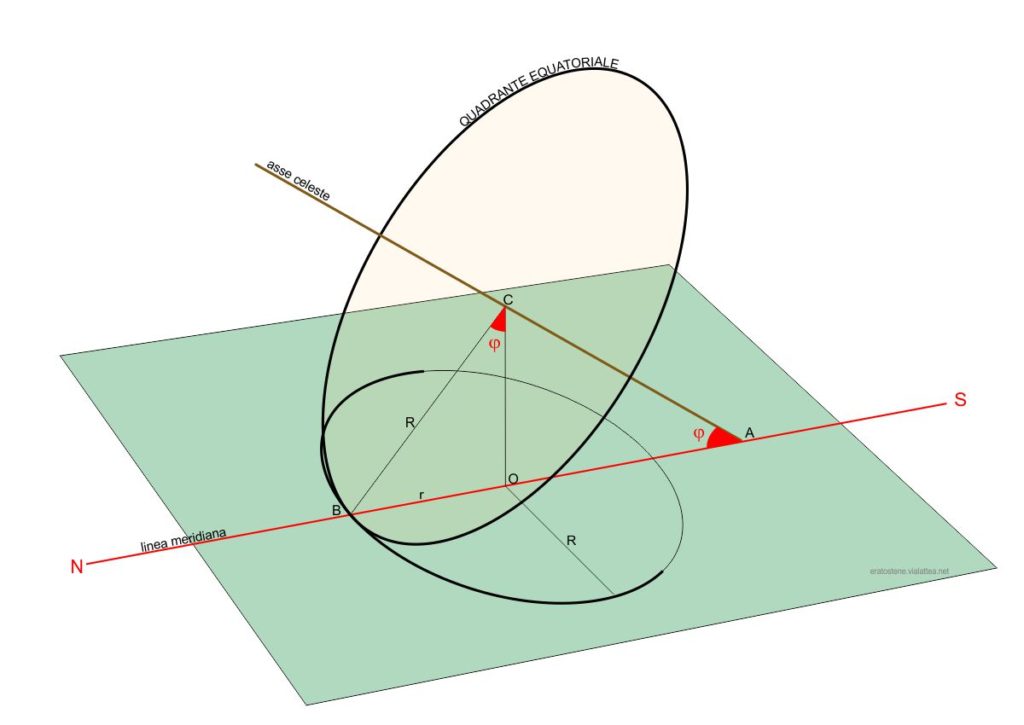
E’ importante considerare con attenzione questo primo disegno. Esso rappresenta innanzitutto l’orologio solare equatoriale orientato.
Per prima cosa vediamo come si ricava il semiasse minore dell’ellisse in funzione della latitudine.
Lo stilo è orientato, come sappiamo, con l’asse celeste. Per fare questo, esso deve formare un angolo $\varphi$ pari alla latitudine con il piano dell’orizzonte e deve trovarsi sul meridiano celeste.
Vediamo qui disegnata sul piano orizzontale l’ellisse dell’orologio analemmatico: essa è la proiezione ortogonale del cerchio del quadrante equatoriale. Perciò il punto $C$ che è il centro di quest’ultimo, si proietta sul piano nel punto $O$ che è il centro dell’ellisse. Il semiasse maggiore $R$ è anche il raggio $BC$. Il semiasse minore $r=\overline{OB}$ dipende dall’inclinazione del quadrante equatoriale e quindi in definitiva dal valore della latitudine $\varphi$. Esso è ricavabile nel modo seguente. Si osservi il triangolo rettangolo $BAC$ retto in $C$: il segmento $CO$ è l’altezza relativa all’ipotenusa, e di conseguenza, il triangolo rettangolo $COB$ retto in $O$ è simile a $BAC$ e ritroviamo l’angolo $\varphi$ anche in $B\hat{C}O$. Ecco la ragione per cui ricaviamo $r$ in funzione del raggio $R$ e della latitudine $\varphi$ da questa formula:
\begin{equation}
\boxed{r=R\cdot\sin\varphi}
\end{equation}
Vediamo ora il perché della formula $Z=R\cdot\cos\varphi\cdot\tan\delta$ utilizzata per costruire le linea delle date in funzione della declinazione del Sole.
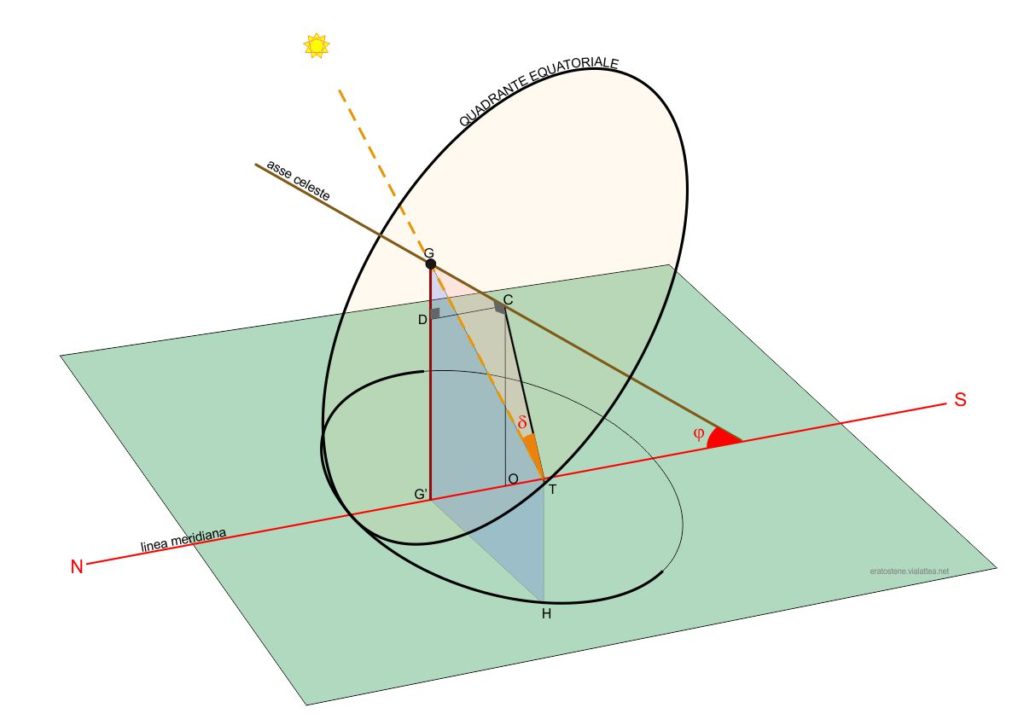
Si consideri un particolare istante del Sole. Lo stilo del quadrante equatoriale (parallelo all’asse celeste) proietta l’ombra $CT$ sul piano del quadrante equatoriale. Ma il Sole ha una declinazione $\delta$ positiva (potrebbe essere un giorno vicino al solstizio di giugno).
Uno dei raggi solari, quello che passa per il punto $G$, raggiunge esattamente il bordo del quadrante equatoriale nel punto $T$. L’angolo $G\hat{T}C$ rappresenta la declinazione del Sole in quell’istante. Il punto $G$ si trova al di sopra del lato nord del quadrante equatoriale. A seconda della declinazione del Sole, il punto $G$ si muove lungo l’asse dello stilo. Quando la declinazione è negativa, il punto $G$ si trova sul lato sud del quadrante, al di sotto del centro $C$.
Agli equinozi il punto $G$ coincide con il centro del quadrante equatoriale e il suo piede $G’$ si trova al centro dell’ellisse.
Il punto $T$ ha la sua proiezione nel piano orizzontale: è il punto $H$ che si trova sull’ellisse della meridiana analemmatica.
Si osservi il segmento verticale $GG’$ e lo si immagini come lo stilo della meridiana analemmatica (o la persona in piedi che funge da stilo). In quell’istante, la sua ombra si proietta sul piano orizzontale formando il segmento $G’H$. E’ l’ombra che indica l’ora sulla meridiana analemmatica. Il problema è questo: per far sì che ciò avvenga, lo stilo verticale $GG’$ deve appoggiare sul terreno in un certo punto $G’$, lungo la linea meridiana, ad una certa distanza dal centro $O$ dell’ellisse. La distanza $\overline{OG’}$ è la distanza $Z$ da calcolare. Come calcolarla?
Il segmento $OG’$ è congruente al segmento $DC$ che fa parte del triangolo rettangolo $GDC$ retto in $D$. L’angolo $G\hat{C}D$ è uguale a $\varphi$. Se conosciamo la lunghezza del segmento $GC$ il problema è risolto. Il segmento $CG$ fa parte di un altro triangolo rettangolo facilmente risolvibile: $GCT$ retto in $C$ di cui conosciamo $CT$ che è il raggio del quadrante equatoriale uguale al semiasse maggiore $R$ dell’ellisse. Conosciamo inoltre l’angolo di declinazione $\delta$. Perciò:
Conoscendo $R=\overline{CT}$ e $\delta$ si calcola $\overline GC$:
$GC = R\cdot\tan\delta$
E ora calcoliamo $\overline{DC}=\overline{G’O}=Z$ risolvendo il triangolo $GDC$:
$Z=\overline{GC}\cdot\cos\varphi$
Sostituendo a $GC$ la formula trovata prima, si ottiene la formula finale che permette di calcolare $Z$ dati la declinazione $\delta$, la latitudine $\varphi$ e il semiasse maggiore dell’ellisse $R$:
\begin{equation}
\boxed{Z=R\cdot\cos\varphi\cdot\tan\delta}
\end{equation}

