Dimostrazione del teorema dei seni
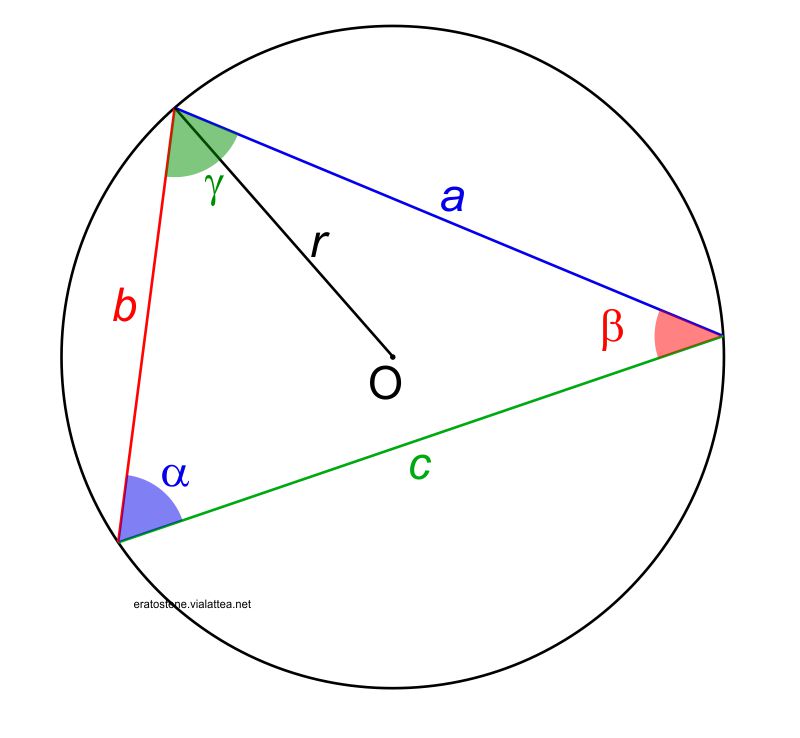
Inscriviamo un triangolo in una circonferenza e così i suoi tre lati diventano altrettante corde di questa circonferenza. Il teorema dei seni si dimostra applicando il teorema della corda che afferma l’uguaglianza:
$$a=2r\cdot\sin\alpha$$
perciò:
$$\frac{a}{\sin\alpha}=2r$$
Ciò è valido anche per gli altri due lati:
$$\frac{b}{\sin\beta}=2r$$
$$\frac{c}{\sin\gamma}=2r$$
Per cui possiamo uguagliare tra loro i tre rapporti ottenendo la formula del teorema dei seni:
$$\boxed{\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}}$$
Dimostrazione del teorema del coseno o di Carnot
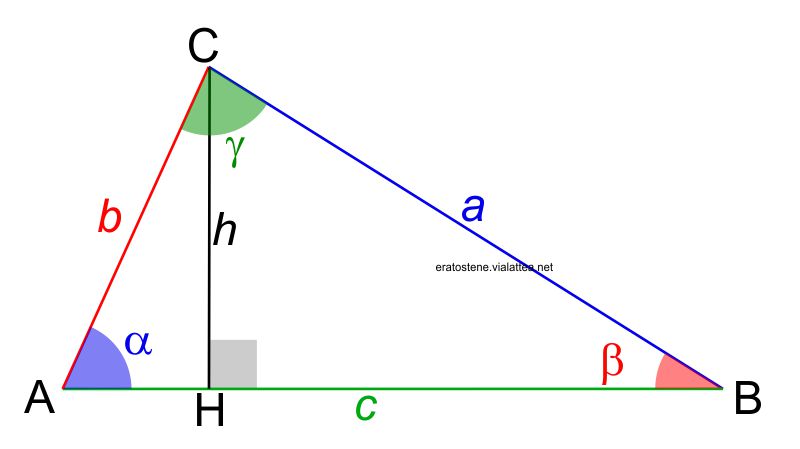
Dimostriamo qui la prima formula di Carnot:
$$a^2 = b^2 + c^2 – 2 b c \cdot \cos\alpha$$
Le altre due si dimostrano con metodi analoghi. $ABC$ è un triangolo qualsiasi di cui tracciamo l’altezza $CH$ relativa alla base $AB$.
Osserviamo il triangolo rettangolo $AHC$ e ricaviamo il suo cateto $CH$ utilizzando il seno di $\alpha$:
(1) ![]()
e, in modo analogo, ricaviamo il cateto $AH$ dello stesso triangolo:
(2) ![]()
Il segmento $HB$ è uguale alla differenza tra la base $AB$ e il segmento $AH$:
$$HB=AB-AH$$
Ora sostituiamo $AH$ con la (2):
(3) ![]()
Applichiamo ora il teorema di Pitagora al triangolo $CHB$:
$$CB^2=CH^2+HB^2$$
Sostituiamo $CH$ con la (1) e $HB$ con la (3):
$$CB^2=(AC\cdot\sin\alpha)^2+(AB-AC\cdot\cos\alpha)^2$$
Elaboriamo ora algebricamente quest’ultima equazione:
$$CB^2=AC^2\cdot\sin^2\alpha+AB^2+AC^2\cdot\cos^2\alpha-2\cdot AB\cdot AC \cdot\cos\alpha$$
Raccogliamo a fattor comune $AC^2$:
$$CB^2=AC^2(\cdot\sin^2\alpha+\cos^2\alpha)+AB^2-2\cdot AB\cdot AC \cdot\cos\alpha$$
Per la relazione fondamentale della trigonometria $cos^2\alpha+\sin^2\alpha=1$, perciò:
$$CB^2=AC^2+AB^2-2\cdot AB\cdot AC \cdot\cos\alpha$$
Infine, sostituendo $CB=a$, $AC=b$ e $AB=c$:
$$\boxed{a^2=b^2+c^2-2bc \cdot\cos\alpha}$$
che è il teorema del coseno che volevamo dimostrare.

