*** torna all’indice ***
Metodo per tracciare le linee orarie estreme
Seguendo il metodo descritto per tracciare le linee orarie, si può facilmente incappare in un problema grafico di difficile soluzione: le linee orarie vicine all’alba e al tramonto potrebbero necessitare di una superficie di disegno troppo estesa rispetto al quadrante che si vuole utilizzare. Ad esempio, per la linea oraria delle ore $7$
(e simmetricamente, quella pomeridiana delle ore $17$) si deve tracciare una semiretta che parte da $H$ e che forma un angolo di $75^\circ$ con la linea meridiana $HO$; il punto di intersezione $T_4$ sulla retta equinoziale risulta troppo lontana dalla linea meridiana. Peggio ancora per la linea oraria delle ore $6:30$ (e $17:30$). Ciò accade in particolare per gli orologi solari posti in località con latitudine elevata dove è anche più utile tracciare le linee delle ore $6$, delle ore $5$, delle ore $4$ e oltre.
Per risolvere il problema senza l’intervento di calcoli trigonometrici, si segua la segua costruzione:
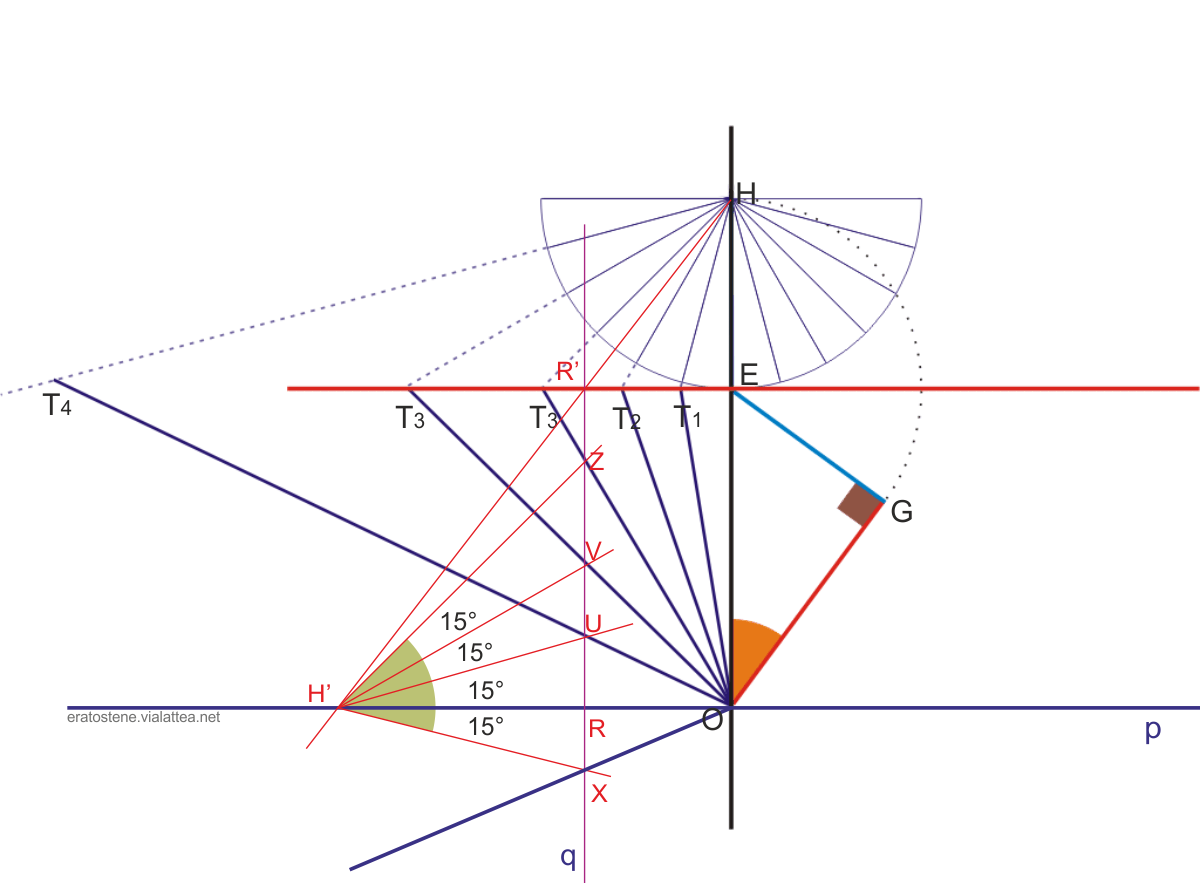
1) Si tracci la retta $p$, passante per $O$ e perpendicolare alla linea meridiana $HO$. Questa retta rappresenta la linea oraria delle $6$ e delle $18$.
2) Si tracci la retta $q$, perpendicolare a $p$, e passante per un punto $R$ qualsiasi ma abbastanza vicino all’origine $O$ dello stilo. La distanza $RO$ va scelta un po’ a tentativi: se è troppo piccola si perde un po’ di precisione nel tracciare le linee orarie, se è troppo grande si risolve solo in parte il problema delle distanze degli intercetti. In ogni caso il punto $R$ deve stare all’interno del quadrante della meridiana che si intende costruire, al massimo sul suo bordo sinistro.
3) La retta $q$ interseca la linea equinoziale nel punto $R’$.
4) Si tracci la semiretta $HR’$ che incontra la retta $p$ nel punto $H’$.
5) Il punto $H’$ diventa un centro sostitutivo del punto $H$, con le medesime funzioni: da $H’$ si possono tracciare le semirette distanziate di $15^\circ$ ciascuna, che vanno ad incontrare la retta $q$ nei punti $Z$, $V$, $U$, $X$, ecc.
6) Le linee orarie “difficili” si possono ora tracciare facilmente, ad esempio:
- $OZ$ e $OV$ sono le linea delle ore $9$ e delle ore $8$, già tracciata precedentemente, tanto per dimostrare che il risultato è identico anche con questo secondo metodo.
- $OU$ è la linea delle ore $7$ che risultava difficile con il primo metodo.
- $OX$ è la linea delle ore 5, utile a latitudini elevate.
*** torna all’indice ***

