*** torna all’indice ***
Le linee diurne
La linea diurna è la traccia percorsa dalla punta dell’ombra dello stilo durante un certo giorno. Come vedremo, le linee diurne sono diverse per ciascun giorno dell’anno e quindi ci permettono di utilizzare la meridiana anche come un calendario.
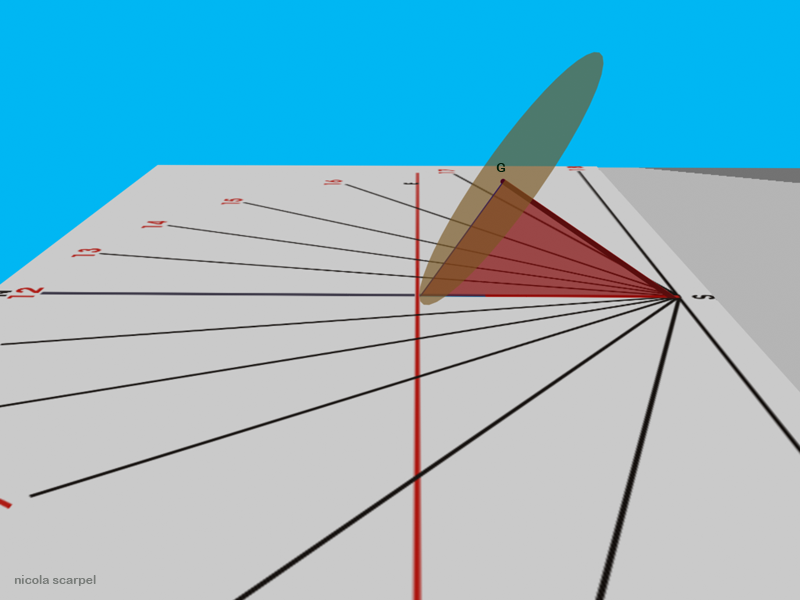
La situazione più semplice da spiegare riguarda i due giorni dell’equinozio, quando la declinazione del Sole è $0^\circ$. Ciò significa che il Sole si trova sul piano dell’equatore che è anche il piano del quadrante dell’orologio. I suoi raggi sono quindi paralleli ad esso. Il quadrante equatoriale stesso, nei giorni degli equinozi, proietta un’ombra rettilinea sul piano orizzontale (vedi le sequenze didattiche per l’orologio equatoriale).
Il piano del quadrante della meridiana equatoriale è rappresentato qui con il cerchio di color ocra. L’arco diurno del Sole inizia esattamente al punto cardinale est e termina al punto cardinale ovest. La retta del raggio di luce che congiunge il Sole con l’estremità dello stilo $G$ si mantiene, nel suo moto diurno, sul piano equatoriale. L’estremità dell’ombra dello stilo sul piano orizzontale percorre perciò la retta equinoziale orientata nella direzione est-ovest. Nel disegno, la retta equinoziale è di colore rosso.
In tutti gli altri giorni dell’anno, il Sole si trova al di sopra o al di sotto del piano equatoriale e il suo arco diurno descrive un qualsiasi parallelo di declinazione diverso dall’equatore.
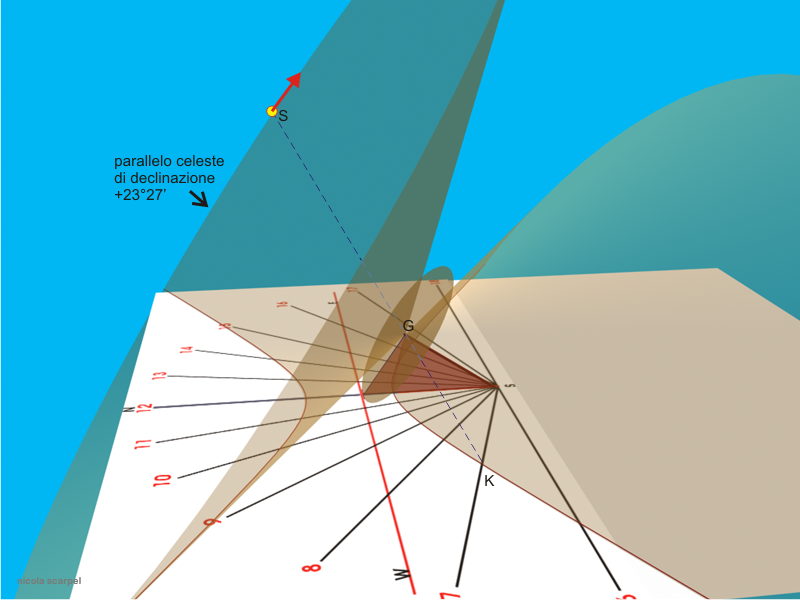
Si consideri un raggio di luce $SK$ che allinea il Sole $S$ l’estremità $G$ dello gnomone (vedi la figura qui sopra a sinistra). E’ interessante riuscire a immaginare il movimento diurno di questo raggio di luce che possiamo immaginare come una lunghissima matita mossa dal Sole: la sua punta scrive sul quadrante orizzontale dell’orologio tracciando una linea diurna, l’altra estremità della matita è tenuta dal Sole che percorre il suo arco diurno ma è vincolata nell’apice $G$ dello stilo che agisce da “perno” del movimento. In termini geometrici, il raggio di Sole descritto è una retta che interseca l’asse celeste (lo stilo) nel punto $G$ e vi ruota attorno generando una superficie conica (cono di declinazione).
L’asse del cono è l’asse celeste; il vertice è la punta dello stilo; la semiapertura è il complementare della declinazione del Sole ($90^\circ-\lvert\delta\rvert$); le due falde della superficie conica corrispondono a due declinazioni opposte del Sole. La minima apertura della superficie conica si ha nei giorni dei solstizi, quando la declinazione raggiunge i valori estremi $+23^\circ27’$ e $-23^\circ27’$. L’immagine di sinistra rappresenta il Sole che percorre la falda conica del solstizio di giugno. Quella del solstizio di dicembre è speculare rispetto al piano dell’equatore.
Per ogni declinazione, l’apice dell’ombra dello stilo (punto $K$) percorre il piano orizzontale e traccia su di esso una linea diurna. Essa è una conica (parabola, iperbole o ellisse) perché è l’intersezione della superficie conica con il piano orizzontale. La linea diurna del solstizio di giugno ha concavità verso sud mentre quella del solstizio di dicembre ha concavità verso nord.

Ecco come si presenta il triangolo gnomonico in rapporto con il piano equatoriale, la linea equinoziale e le due falde coniche dei solstizi.

Ecco come si presenta la meridiana orizzontale arricchita da tre linee diurne significative: la retta equinoziale, la linea diurna del solstizio di giugno (verso sud) e la linea diurna del solstizio di dicembre (verso nord). Nel disegno, la meridiana indica all’incirca le ore solari 10:30 e, dato che la punta dello stilo si trova a nord della retta equinoziale ci troviamo nell’arco dell’anno che va dall’equinozio di settembre all’equinozio di marzo.
La punta dell’ombra non supererà mai i limiti delle due linee diurne solstiziali e quindi le parti di rette orarie che escono da tali limiti (sia a sud della linea del solstizio di giugno che a nord di quella del solstizio di dicembre) vanno cancellate perché inutili.

Come tracciare le linee diurne? Si consideri inizialmente la situazione più semplice: il mezzogiorno solare. I raggi solari proiettano l’ombra dello stilo lungo la linea meridiana EO. Nell’estate boreale (declinazione solare $\delta\simeq+23^\circ\!\text{,5}$) l’apice dell’ombra si proietta in $K’$ dove si trova uno dei vertici dell’iperbole. In inverno (declinazione $\delta\simeq-23^\circ{,5}$) l’apice dello stilo si proietta in $K$ dove si trova l’altro vertice.
Agli equinozi l’apice dell’ombra cade in $E$ che è un punto già definito nella costruzione del triangolo stilare.

Il prossimo passo è considerare l’ombra di una certa ora, sempre all’equinozio. In questa immagine la semiretta $OT$ corrispondente alla linea oraria delle ore 10 solari in un giorno equinoziale (la superficie conica è degenerata in un piano rappresentato dal cerchio e l’apice $T$ dell’ombra cade sulla linea equinoziale):
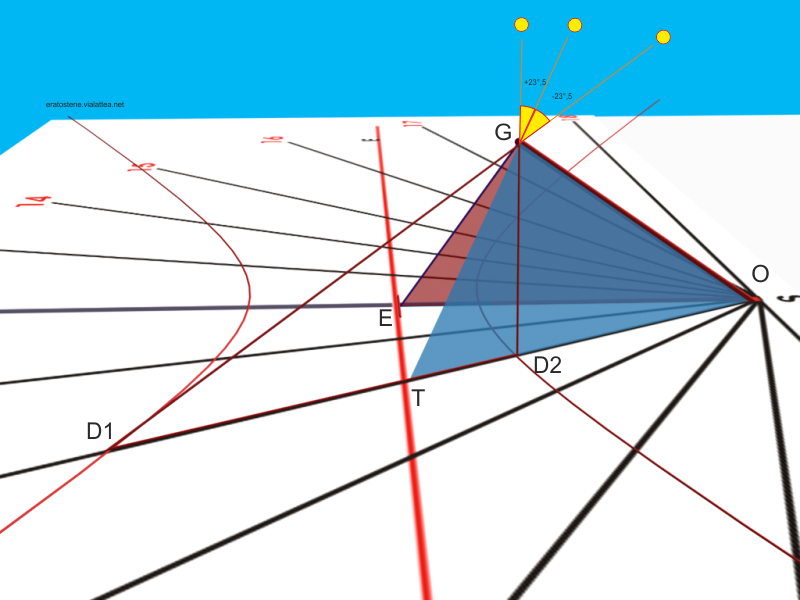
Esaminando ora la stessa situazione oraria, anche per gli altri due momenti dell’anno, i solstizi, la situazione è la seguente. Quando il Sole è al solstizio di dicembre (declinazione $\delta\simeq-23^\circ{,5}$) alle ore 10 solari, il suo raggio proietta l’ombra dell’apice $G$ dello stilo nel punto $D_1$ del quadrante. Il punto $D_2$ invece rappresenta l’apice dell’ombra nel giorno del solstizio di giugno, alla stessa ora.

Come si vede nella tavola a fianco, se si ribalta il triangolo $OGD_1$ sul piano orizzontale facendolo ruotare attorno al lato $OD_1$, si otteniamo il nuovo triangolo $OG_2D_1$. Manteniamo traccia anche dei segmenti originali $GT$ e $GD_2$ che, nel nuovo triangolo, diventano $G_2T$ e $G_2D_2$.
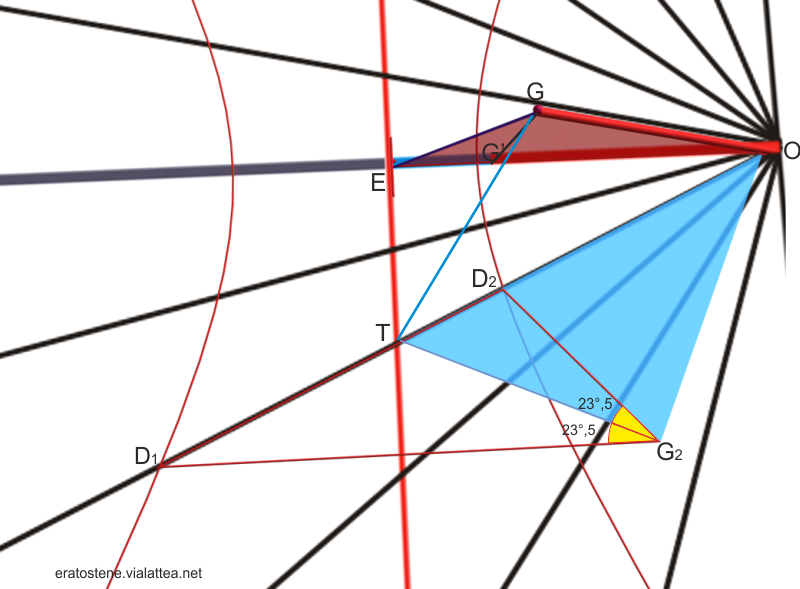
Osservando dall’alto, riconosciamo nel triangolo $OG_2D_1$, gli elementi che ci interessano ai fini della costruzione grafica:
Gli angoli $TG_2D_1$ e $TG_2D_2$ sono entrambi di $23^\circ\!\text{,5}$.
Il segmento $OG_2$ è congruente a $OG$ e rappresenta la lunghezza dello stilo
e, ovviamente, anche il segmento $G_2T$ è congruente con $GT$.
Ora possediamo tutti gli elementi concettuali per iniziare la costruzione grafica.
*** torna all’indice ***

