L’angolo parallattico, o angolo dell’astro o angolo di posizione è l’angolo sferico che ha per vertice l’astro e per lati il verticale dell’astro e l’orario dell’astro (vedi il triangolo di posizione).
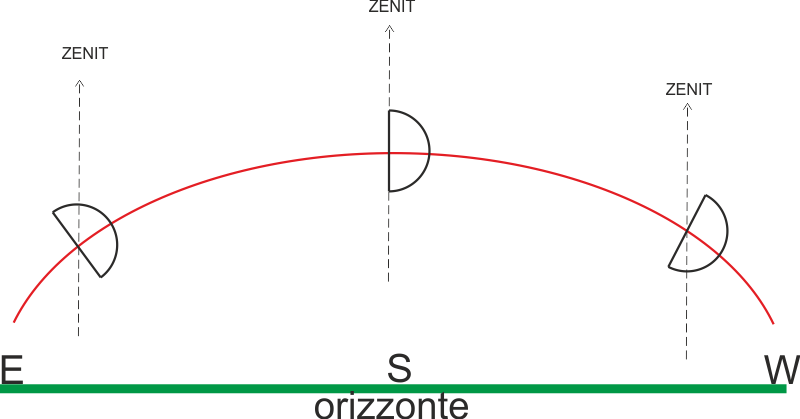
E’ un indicatore dell’inclinazione in cui ci appare un corpo celeste, rispetto allo zenit, nel corso del suo moto apparente diurno.
Si osservi la Luna al primo quarto nel corso del suo moto apparente lungo l’arco diurno. Quando essa si trova nell’emisfero orientale l’intera “gobba” è rivolta generalmente in alto, mentre quando la Luna si avvia al suo tramonto è inclinata verso il basso. Ciò accade non solo con la Luna ma per tutti i corpi celesti, come pure alle configurazioni delle costellazioni la cui “inclinazione” varia a seconda della loro posizione lungo l’arco diurno.
L’espressione “angolo parallattico” non ha nulla a che fare con il fenomeno di parallasse. Il significato dell’aggettivo parallattico si riferisce, in questo caso, alla deviazione dell’asse dei corpi celesti che si manifesta nel corso del loro moto diurno lungo i circoli dei paralleli di declinazione (vedi il significato etimologico di parallasse).
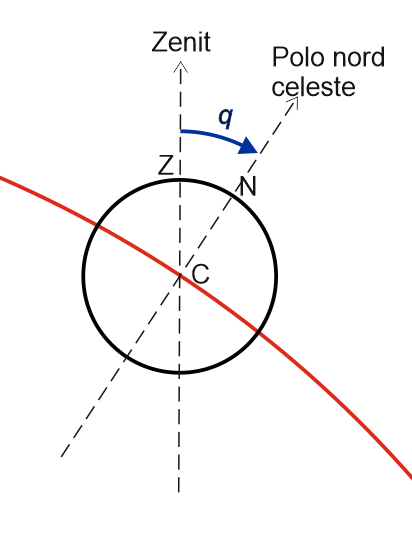
Se consideriamo il disco di un qualunque corpo celeste di centro $C$ che percorre un tratto del suo arco diurno (la curva di colore rosso, che è un parallelo di declinazione), la direzione $CZ$ è un tratto del verticale dell’astro e punta allo zenit, mentre la direzione $CN$ è un tratto di orario dell’astro, perpendicolare all’arco diurno, che punta al polo nord celeste. Il punto $Z$ è il punto del bordo del disco che è rivolto allo zenit (punto zenitale del disco) e il punto $N$ è quello rivolto al polo nord celeste (punto nord del disco). L’angolo parallattico $q$, è l’angolo compreso tra queste due direzioni, ed è convenzionalmente positivo quando l’astro ha già attraversato il meridiano e negativo prima di attraversarlo. Quando l’astro è al meridiano $q=0^\circ$.
L’angolo parallattico si calcola in funzione della latitudine dell’osservatore $\varphi$, dell’angolo orario $H$ e della declinazione $\delta$ dell’astro:
$$\tan q = \frac{\sin H}{\tan\varphi\cdot\cos\delta-\sin\delta\cos H}$$~~~GLOSSARIO~~~