- Metodo di Eratostene
- Determinazione della distanza in linea d’aria
- De Sphaera
- Il metodo di Al-Biruni
La misurazione della Terra è un a interessante esperienza didattica proposta dalla Rete di Eratostene. Si svolge con la collaborazione di più scuole. Il coordinamento avviene per mezzo di una mailing-list dedicata.
Questa pagina riassume le informazioni essenziali e i riferimenti per la realizzazione dell’esperimento.
1. Cosa fece Eratostene…
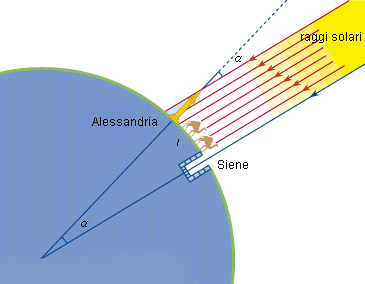Eratostene, nel III secolo avanti Cristo, realizzò la prima misurazione delle dimensioni della Terra confrontando tra loro le altezze del Sole misurate nello stesso giorno, a mezzogiorno, tra due località abbastanza lontane, poste una a nord (Alessandria) e una a sud (Siene). Misurò una differenza di 7,2°, pari a un cinquantesimo dell’angolo giro. Dato che questo angolo corrisponde anche all’angolo compreso tra i raggi al centro della Terra che passano per le due città, anche la loro distanza effettiva alla superficie doveva essere pari a un cinquantesimo della circonferenza terrestre. Semplice come una una moltiplicazione!
Vedi una pagina di approfondimento sul suo metodo.
Vedi: un modello GeoGebra
2. Cosa facciamo noi…
Alle nostre latitudini i raggi solari non raggiungono mai la verticalità. D’altra parte ciò che conta è la differenza di inclinazione dei raggi, come vengono osservati da due località (scuole) poste una a nord e l’altra a sud, possibilmente vicine in longitudine. Proponiamo quindi di misurare contemporaneamente l’altezza del Sole e confrontare i due risultati. Per maggior precisione, la misurazione dovrebbe avvenire nel momento della culminazione del Sole, cioè nel momento del mezzogiorno solare vero (non quello indicato dagli orologi meccanici, bensì il mezzogiorno delle meridiane). L’altezza del Sole si può misurare con alcuni semplici metodi basati sull’ombra proiettata da uno gnomone verticale. Il metodo richiede la costruzione di altrettanto semplici strumenti. Rimane comunque a discrezione delle singole scuole la scelta di un metodo preferito. Dal confronto delle altezze e dalla distanza di due località, con dei semplicissimi calcoli si ottiene una stima della circonferenza terrestre.
3. Costruire gli strumenti ed eseguire la misurazione
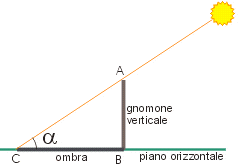Come abbiamo accennato, il metodo di misurazione si basa sulla proiezione dell’ombra di uno gnomone verticale sul piano orizzontale. Lo scopo è quello di misurare l’altezza del Sole rispetto all’orizzonte (angolo 
).
Nella pagina che descrive in dettaglio questa tecnica (vedi misurare l’altezza del Sole) proponiamo alcuni metodi più o meno complessi sia dal punto di vista della costruzione che dal punto di vista dell’impiego didattico. Nel caso più semplice si effettua una misura diretta con un quadrante mobile oppure una misura indiretta basata sull’ombra proiettata da uno gnomone verticale. Nel caso dell’utilizzo di uno gnomone la misura dell’angolo può essere determinata da un semplice calcolo trigonometrico (
) oppure dall’uso di un goniometro su un disegno che riproduce schematicamente il triangolo 
una volta misurati l’altezza dello gnomone e la lunghezza dell’ombra. Nella scelta del metodo di misurazione, proponiamo un accordo di omogeneità tra le scuole che misurano. In questo modo possiamo cercare di valutare e confrontare la validità di ciascun metodo.
E’ importante sapere che la misurazione deve essere eseguita quasi contemporaneamente e deve coincidere con il mezzogiorno solare vero (generalmente diverso dal tempo civile). Il mezzogiorno solare vero è il momento del transito del Sole al meridiano del luogo. Tale istante varia a seconda della longitudine del luogo e del giorno di osservazione e può essere facilmente determinato utilizzando il nostro modulo di calcolo.
4. Organizzare e scambiare i dati
Di norma, ogni classe si divide in gruppetti (postazioni) che eseguono un certo numero di misurazioni. Si consiglia di approfittare di questa esperienza per trattare statisticamente le misurazioni (nel caso più semplice si calcola solo la media aritmetica).Il valore ottenuto va confrontato con quello della scuola gemella allo scopo di calcolare la circonferenza terrestre.
5. Calcolare la circonferenza terrestre
Si sottraggono i due valori dell’altezza del Sole indicati dalle due scuole. Si calcola quante volte questa differenza sta nell’angolo giro. Quindi si moltiplica questo quoziente per la distanza in chilometri tra le due scuole. Il risultato è la lunghezza in chilometri della circonferenza terrestre.
Se 
è la differenza tra le altezze del Sole in gradi e 
è distanza in chilometri tra le due località, la circonferenza terrestre si calcola:
Questa formula si può pensare anche come ricavata dal calcolo dell’incognita 
della proporzione:
Infatti l’ampiezza dell’angolo al centro è direttamente proporzionale alla lunghezza dell’arco di circonferenza corrispondente.
N.B.: la distanza tra due località si determina utilizzando una carta geografica con rapporto di scala massimo di 1:3.000.000 oppure la funzione righello di Google Earth
Quasi mai le due località sono allineate con precisione sufficiente lungo uno stesso meridiano. Se la differenza di longitudine è consistente è necessario considerare piuttosto la distanza tra i loro paralleli.
6. Documentazione dell’esperienza
Le scuole che lo desiderano possono produrre delle relazioni di documentazione dell’esperienza che verranno pubblicate nel nostro sito.
|