
Abu Rayhan (Muhammad ibn Ahmad) al-Biruni nacque a Kath (Corasmia) nel 973 d.C. e morì a Ghazni (Korasan) nel 1050 d.C. Fu un grande matematico, filosofo, scienziato, storico e linguista persiano. E’ considerato da molti il fondatore dell’indologia, della geodesia e dell’antropologia. Parlava fluentemente il persiano, l’arabo, il turco, il sanscrito, il greco, l’ebraico, il siriano e vari altri linguaggi locali delle cui letterature era un grande conoscitore. Non solo possedeva tutti i ben noti libri di astronomia scritti nell’area che si estende dal Mar Mediterraneo al Golfo del Bengala, inclusi tutti gli autori greci, indiani e musulmani dalla Spagna all’Egitto, ma scrisse in modo prolifico in tutti i rami della conoscenza (cartografia, geografia, etnografia, storia, filosofia, matematica, astronomia e scienza in generale) producendo un totale di circa 180 opere, alcune purtroppo andate perdute.
Nell’immagine a fianco al-Biruni è raffigurato in un francobollo russo del 1973.
Al-Biruni è famoso anche per la sua misurazione del raggio terrestre la cui precisione rimase imbattuta fino alle misurazioni occidentali del XVI secolo e il cui metodo era caratterizzato da una notevole originalità rispetto ai metodi dei suoi predecessori.
Un secolo prima di Al-Biruni, il sultano al-Mamun (786-833 d.C.) incaricò vari gruppi di geometri di eseguire la misurazione della Terra. Il loro metodo era analogo in linea di principio con quello di Eratostene: mettere in rapporto la differenza di altezza meridiana del Sole misurata da due luoghi di osservazione posti lungo uno stesso meridiano. Le operazioni consistevano nell’impiegare due squadre che partivano da una certa località in due direzioni opposte, una squadra verso nord e l’altra verso sud. Ogni squadra misurava quotidianamente la distanza percorsa e l’altezza meridiana del Sole per poter confrontare in seguito le coppie di misurazioni simultanee. Due squadre partirono da una località del deserto di Sinjar (nell’attuale Iraq). Altre spedizioni operarono nei pressi di Tadmor nell’attuale Siria.
Ai tempi di Al-Biruni, la lunghezza universalmente accettata, derivata dalle misurazioni del sultano al-Mamun, era di $56\frac{2}{3}$ miglia arabe per un grado di meridiano.
Le unità di misura di lunghezza dell’antico Islam erano la parasanga, formata da tre miglia arabe. Ogni miglio equivaleva a $4000$ cubiti e ogni cubito a 24 dita. Nel nostro sistema metrico queste unità potevano valere:
1 parasanga = $\text{5 916 }m$
1 miglio = $\text{1 972 }m$
1 cubito = $\text{493 }mm$
Se calcoliamo la lunghezza del grado di meridiano terrestre ottenuto da Al-Biruni in base a questa stima delle unità di misura storiche otteniamo $\text{111,747 }km$, un valore molto vicino alla misura attuale che, per le latitudini comprese tra $35^\circ$ e $36^\circ$ nord, è di $\text{110,950 }km$.
Al Biruni voleva ripetere l’esperimento, ma fu stato ostacolato da una mancanza di supporto. Erano necessarie notevoli risorse per attraversare lunghi tratti di deserto e la spedizioni non erano prive di pericoli. Dopo un tentativo con risultati poco incoraggianti effettuato nella terra dei Turchi, non riuscì più ad ottenere i fondi necessari. Invece di rinunciare a causa delle difficoltà incontrate, al-Biruni inventò un metodo che non necessitava più di lunghe e pericolose cammiate nel deserto, bensì sfruttava un’ingegnosa applicazione di leggi geometriche che permettevano ad una persona, da sola, di misurare la Terra. Il metodo consisteva nel combinare due misurazioni: quella dell’altezza di una montagna e quella della depressione dell’orizzonte.
I metodi per misurare l’altezza di una montagna erano ben noti al tempo di Al Biruni. Sono metodi utilizzati ancora oggi, anche se l’approccio matematico è diverso. Essi sfruttano l’effetto di parallasse ottenuto traguardando l’oggetto lontano da due punti di osservazione diversi. In questo modo si possono misurare non solo le distanze di oggetti irraggiungibili, ma anche le loro dimensioni.
Al Biruni scelse una collina che si trovava nell’attuale Pakistan, nei pressi del forte di Nandana, sui primi contrafforti della catena del Karakorum, affacciata sull’estesa regione pianeggiante del fiume Jhelum.
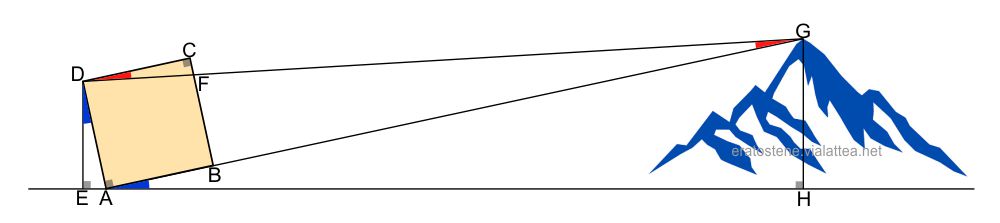
In una località della pianura dalla quale si vedeva la collina prescelta, costruì uno strumento di forma quadrata $ABCD$ e lo posizionò verticalmente in direzione della cima. Il quadrato era inclinato in modo tale che il lato $AB$ fosse allineato con la cima $G$. Traguardando dal vertice $D$, la cima non era allineata con $C$ ma con un punto $F$ del lato $CB$.
Il problema di calcolare l’altezza $GH$ senza poter misurare la distanza $AH$ è risolvibile in vari modi (*). Qui scegliamo il più semplice, che non scomoda la trigonometria, e si basa su un gioco di triangoli rettangoli simili. Non è difficile scoprire che il triangolo $DCF$, retto in $C$, è simile al triangolo $DAG$ retto in $A$. Possiamo perciò scrivere l’uguaglianza dei due rapporti:
$$\frac{AG}{DA}=\frac{DC}{CF}$$
Se misuriamo le lunghezze $DA$, $DC$ e $CF$ possiamo calcolare $AG$:
$$AG=\frac{DA\cdot DC}{CF}$$
Nella figura scopriamo anche un’altra similitudine del triangolo $DEA$ retto in $E$ con il triangolo $GHA$ retto in $GH$. Possiamo scrivere perciò l’uguaglianza:
$$\frac{GH}{AG}=\frac{EA}{DA}$$
Misurando $EA$ possiamo calcolare l’altezza della collina $GH$ perché gli altri termini $AG$ e $DA$ sono già noti:
$$GH=\frac{EA\cdot AG}{DA}$$
Il passo successivo fu quello di raggiungere la cima di questa collina e di misurare, da quel punto di osservazione, la depressione dell’orizzonte, cioè l’inclinazione del limite visibile della pianura rispetto al piano orizzontale definito da una livella.

Al Biruni utilizzò probabilmente un astrolabio dotato di alidada, tenuto appeso all’anello per mantenere la corretta verticalità della scala graduata.
Nello schema a fianco troviamo che un triangolo rettangolo ci viene ancora in aiuto. Il punto $T$ è il limite dell’orizzonte visibile dall’osservatore $G$ posizionato sulla cima della collina e $O$ è il centro della Terra. L’angolo $\theta$, compreso tra il piano orizzontale $GK$ e la linea di vista $GT$, è uguale all’angolo $T\widehat{O}H$ che ha per vertice il centro della Terra e i cui lati passano per l’osservatore $G$ e per il limite della linea di vista $(T)$. Infatti, l’angolo $K\widehat{G}O$ è retto e $\theta$ è il complemento a $90^\circ$ dell’angolo $T\widehat{G}O$.
Il problema consiste nel calcolare il raggio della Terra $r=OH=TO$ conoscendo i due parametri che sono stati misurati: l’angolo $\theta$ e l’altezza della collina $h=GH$. E’ facilmente risolvibile utilizzando una funzione trigonometrica: il coseno dell’angolo $\theta$ è uguale al rapporto tra il cateto adiacente $TO$ e l’ipotenusa $OG$. Possiamo scrivere l’uguaglianza:
$$\cos\theta=\frac{TO}{OG}=\frac{r}{r+h}$$
Da questa espressione ricaviamo $r$ ottenendo la formula che divenne famosa:
$$\boxed{r=\frac{r\cdot\cos\theta}{1-\cos\theta}}$$
Al Biruni trovò che l’angolo $\theta$ era uguale a $0^\circ 34’$, e calcolò un raggio della Terra di $\text{12 851 370}$ cubiti pari a $\text{6 336 }km$. Se avesse avuto a disposizione una calcolatrice scientifica, con questi dati avrebbe ottenuto un raggio di $\text{13 331 728}$ cubiti pari a $\text{6 573 }km$. In ogni caso un risultato straordinario e forse anche troppo preciso! La stima attuale del raggio terrestre alla latitudine di Nandana ($32^\circ 43’$) è infatti di $\text{6 354 }km$ ma bisogna considera che Al Biruni non ha tenuto conto dell’effetto di rifrazione atmosferica che non era noto a quei tempi. La rifrazione “solleva” l’orizzonte reale producendo un errore poco prevedibile, che dipende dalle condizioni atmosferiche. Anche un piccolo errore nella misura della depressione dell’orizzonte corrisponde ad una grande differenza nel calcolo del raggio terrestre!
- Metodo di Eratostene
- Determinazione della distanza in linea d’aria
- De Sphaera
- Il metodo di Al-Biruni
(*)
Misurare una montagna con la triangolazione
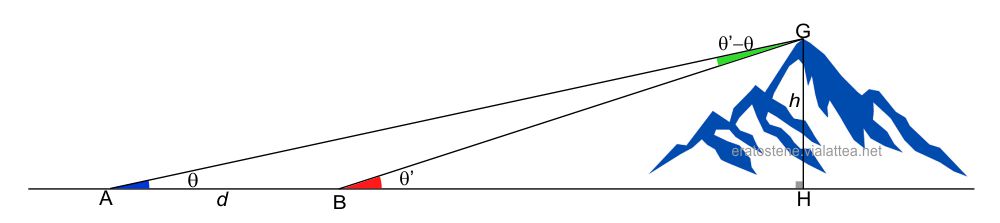
Un’alternativa attuale al metodo di Al Biruni è quella di misurare la direzione della cima $G$ del rilievo da due punti di osservazione $A$ e $B$, situati entrambi sulla pianura orizzontale, e allineati alla verticale $GH$. La distanza $d$ dev’essere facilmente misurabile.
Si misurano gli angoli $\theta$ e $\theta’$ che sono le altezze angolari della cima $G$ dai due punti di osservazione. L’angolo $A\widehat{G}B=\theta’-\theta$ è l’angolo parallattico della cima. Si tratta ora di trovare un metodo matematico per calcolare $h$ in funzione di $d$, $\theta$ e $\theta’$. Applicando il teorema dei seni sul triangolo $ABG$ possiamo scrivere:
$$\frac{BG}{\sin\theta}=\frac{d}{\sin(\theta’-\theta)}$$
da cui possiamo ricavare $BG$:
$$BG=\frac{d\cdot\sin\theta}{\sin(\theta’-\theta)}$$
Ora, osservando il triangolo rettangolo $GHB$ vediamo che:
$$h=BG\cdot\sin\theta’$$
Non ci resta che sostituire $BG$ ottenendo la formula che serve al nostro scopo:
$$\boxed{h=\frac{d\cdot\sin\theta’\cdot\sin\theta}{\sin(\theta’-\theta)}}$$

