La parola orizzonte deriva dal latino horizon e dall’espressione greca ὁρίζων κύκλος che significa “circolo che divide, o che limita”. Anche nel linguaggio comune l’orizzonte è quella “circonferenza” che sembra dividere il cielo dalla terra. In astronomia questo termine si arricchisce e si articola in significati più complessi che descriviamo qui.
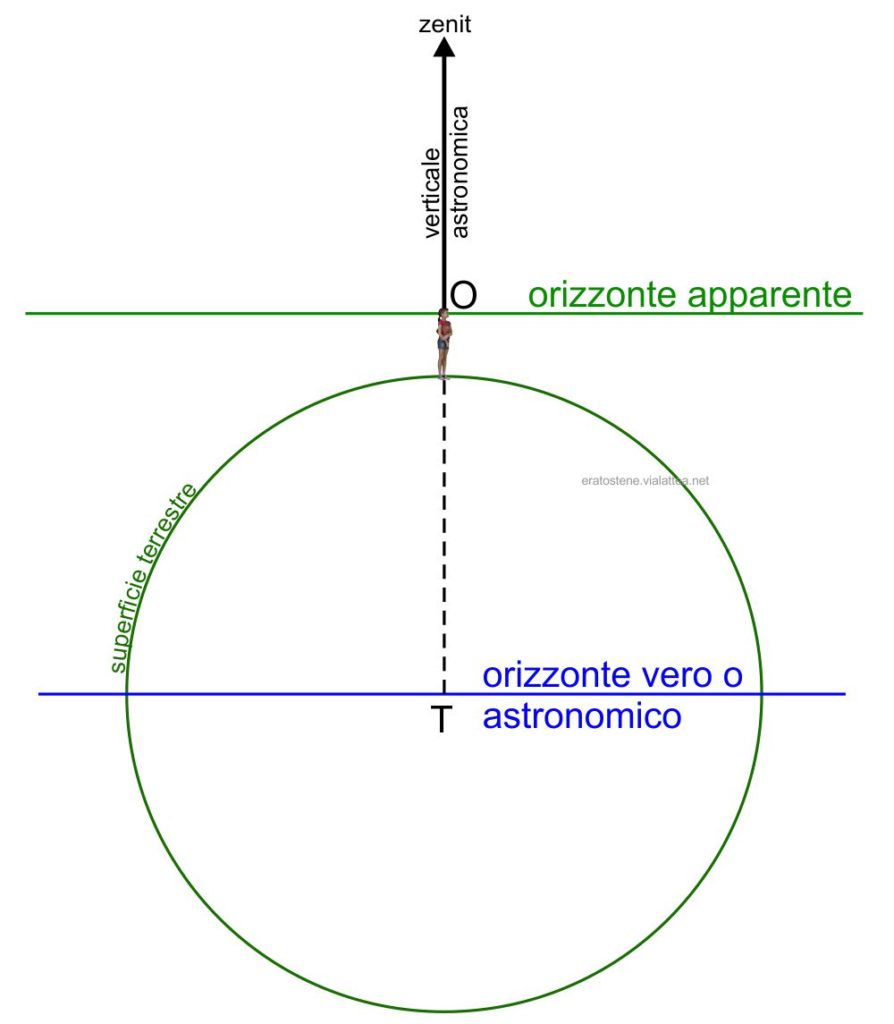
L’orizzonte che interessa maggiormente l’astronomo è l’orizzonte apparente: un piano perpendicolare alla verticale, che passa per l’occhio dell’osservatore $(O)$.
Un altro orizzonte importante è l’orizzonte vero o astronomico. E’ un piano sempre perpendicolare alla verticale dell’osservatore, quindi è parallelo all’orizzonte apparente, ma passa per il centro $T$ della Terra. Nell’ipotesi semplificativa di una Terra di forma sferica, la verticale astronomica coincide con il raggio geocentrico (vedi Le verticali e i sistemi di coordinate terrestri).
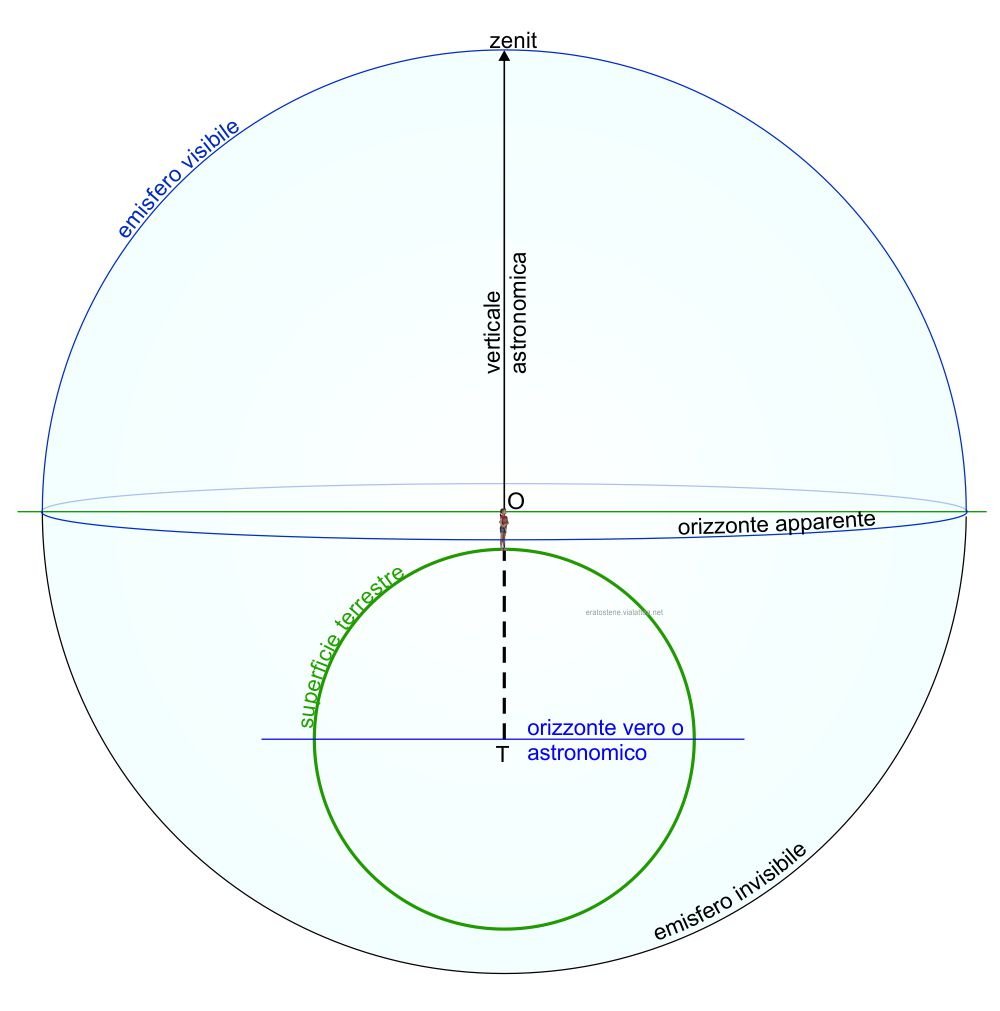
Il piano dell’orizzonte apparente interseca la sfera celeste locale o topocentrica (cioè quella che ha per centro l’occhio dell’osservatore $O$) formando un cerchio massimo chiamato anch’esso orizzonte apparente.
A sua volta, il piano dell’orizzonte astronomico interseca la sfera geocentrica (cioè quella che ha per centro il centro della Terra $T$) lungo un cerchio massimo che porta lo stesso nome o, talvolta, orizzonte razionale (non rappresentato in questa figura).
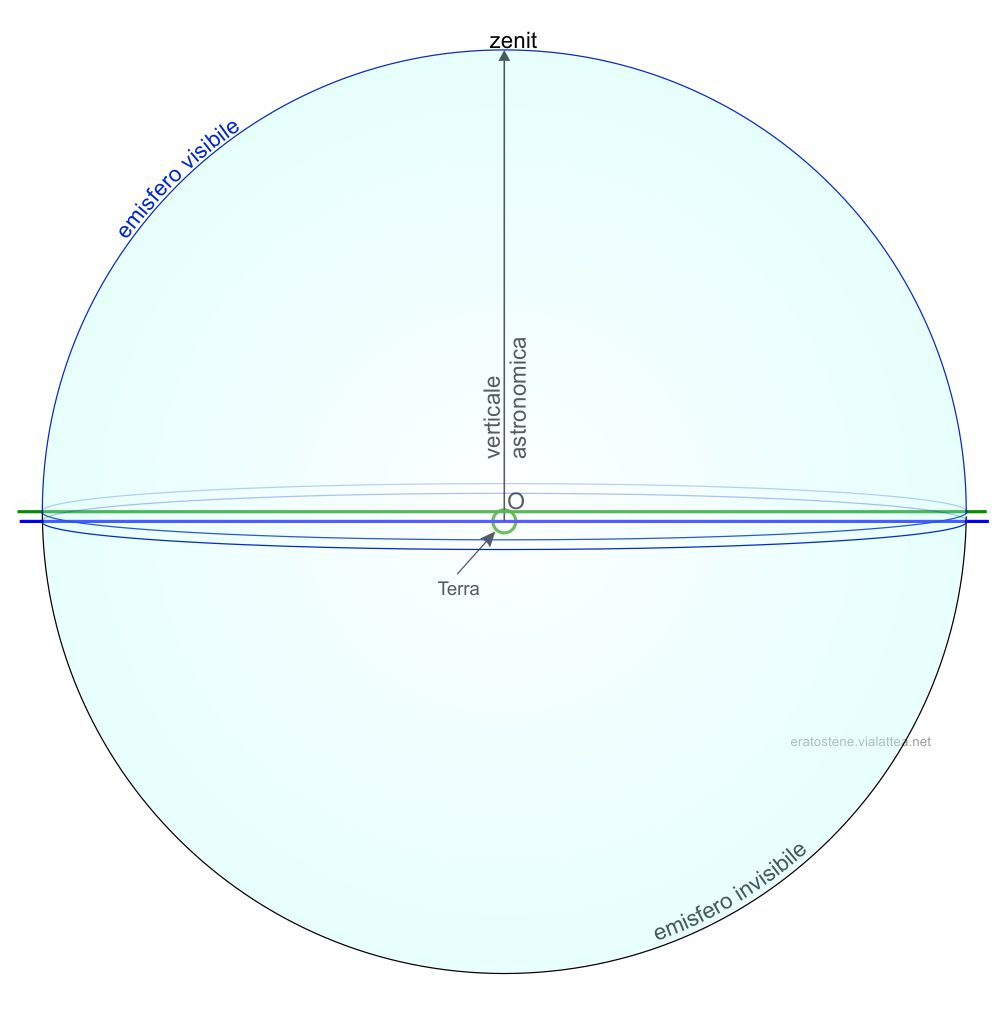
Date le dimensioni indefinitamente grandi della sfera celeste rispetto alla Terra, l’orizzonte apparente e l’orizzonte astronomico praticamente coincidono. Ciò è vero per i corpi celesti molto lontani, come ad esempio le stelle, che non risentono della parallasse diurna. Solo per i corpi celesti del Sistema Solare, in particolare per la Luna e per i pianeti interni, è necessario tener conto della differenza tra i due orizzonti.
Questo tipo di orizzonte (sia esso apparente o astronomico) rappresenta il piano fondamentale per il sistema di coordinate altazimutali. L’altezza di un astro si definisce come la sua distanza angolare rispetto ad esso. Il verticale dell’osservatore diventa l’asse di questo sistema; lo zenit e il nadir sono i suoi poli.
L’orizzonte definito in questo modo, divide la sfera celeste in due emisferi: l’emisfero visibile è quello che contiene lo zenit, mentre l’emisfero invisibile è quello che contiene il nadir.
Ritornando sulla Terra, è importante considerare la quota dell’osservatore in relazione ad un’altra serie di definizioni di orizzonti.
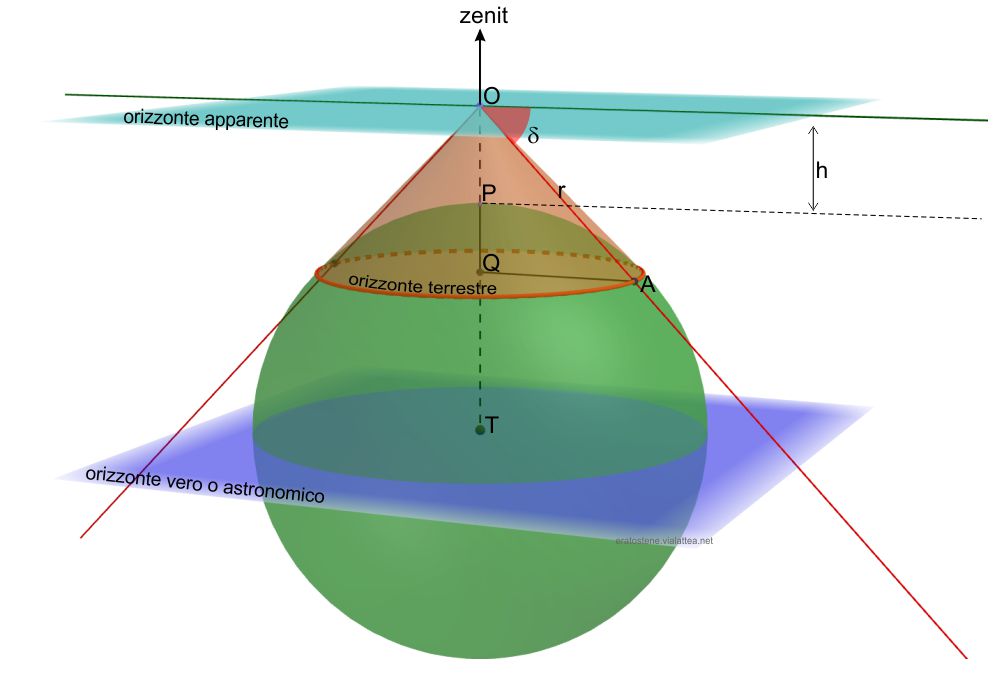
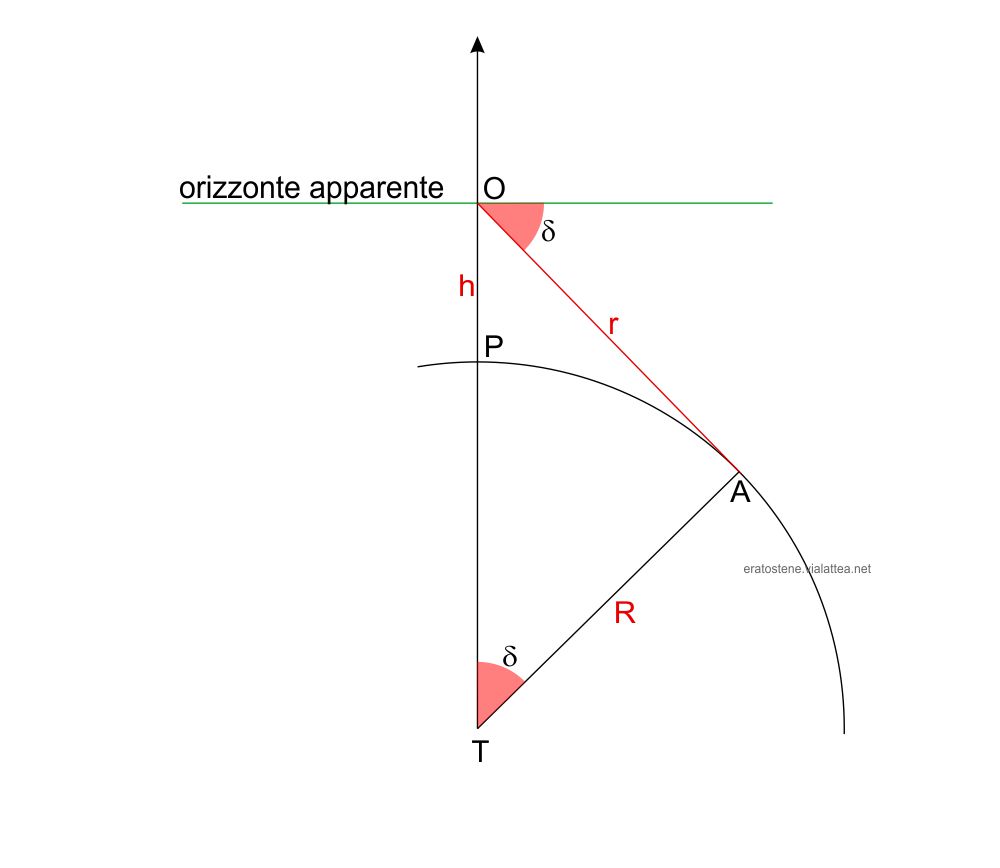
In questo schema, l’occhio dell’osservatore $O$ si trova ad una quota $OP=h$ rispetto alla superficie terrestre. Maggiore è la sua quota, più estesa è la calotta di superficie terrestre che egli riesce a vedere. Il “bordo” visibile estremo della superficie terrestre può essere rappresentato da un cerchio e definibile geometricamente. Questo cerchio è chiamato orizzonte terrestre.
Se si approssima la forma della Terra ad una sfera e se non si tiene conto dell’effetto della rifrazione atmosferica, l’orizzonte terrestre è un cerchio che determina il limite teorico di questa calotta di superficie visibile. Possiamo costruire idealmente un cono che ha per vertice l’osservatore $O$ e per base l’orizzonte terrestre. L’apotema $OA=r$ di questo cono è chiamato raggio d’orizzonte.
Un fenomeno importante che si verifica in quota è che l’osservatore non vede l’orizzonte terrestre al livello dell’orizzonte apparente, ma lo vede al di sotto di esso secondo un angolo $\delta$ chiamato depressione dell’orizzonte.
Il raggio d’orizzonte è tanto più grande quanto maggiore è la quota $h$ dell’osservatore. Per fare un esempio, il raggio d’orizzonte $r$ per un uomo di media statura $h=\text{1,70 } m$, è di $\text{4,7 }km$. Da $\text{100 }m$ di quota la visibilità arriva a $\text{36 }km$ di distanza.(1)
La proiezione dell’orizzonte terrestre $AB$ sulla sfera celeste locale è un circolo minore $A’B’$, parallelo al circolo massimo dell’orizzonte apparente. E’ chiamato orizzonte reale o sensibile. Si deduce da questo schema che la parte di sfera celeste che vede un osservatore in quota è maggiore dell’emisfero visibile.
Per un osservatore che viaggia con un’astronave e che si allontana ad una quota $h$ molto grande rispetto al diametro terrestre, la porzione della sfera celeste visibile sarà quasi completa, a parte un piccolo cerchio nascosto dal disco opaco della Terra che corrisponderà all’orizzonte terrestre.
Come abbiamo accennato, le considerazioni fatte fino ad ora non tengono conto di un fenomeno importante dovuto alla presenza dell’aria: la rifrazione atmosferica.
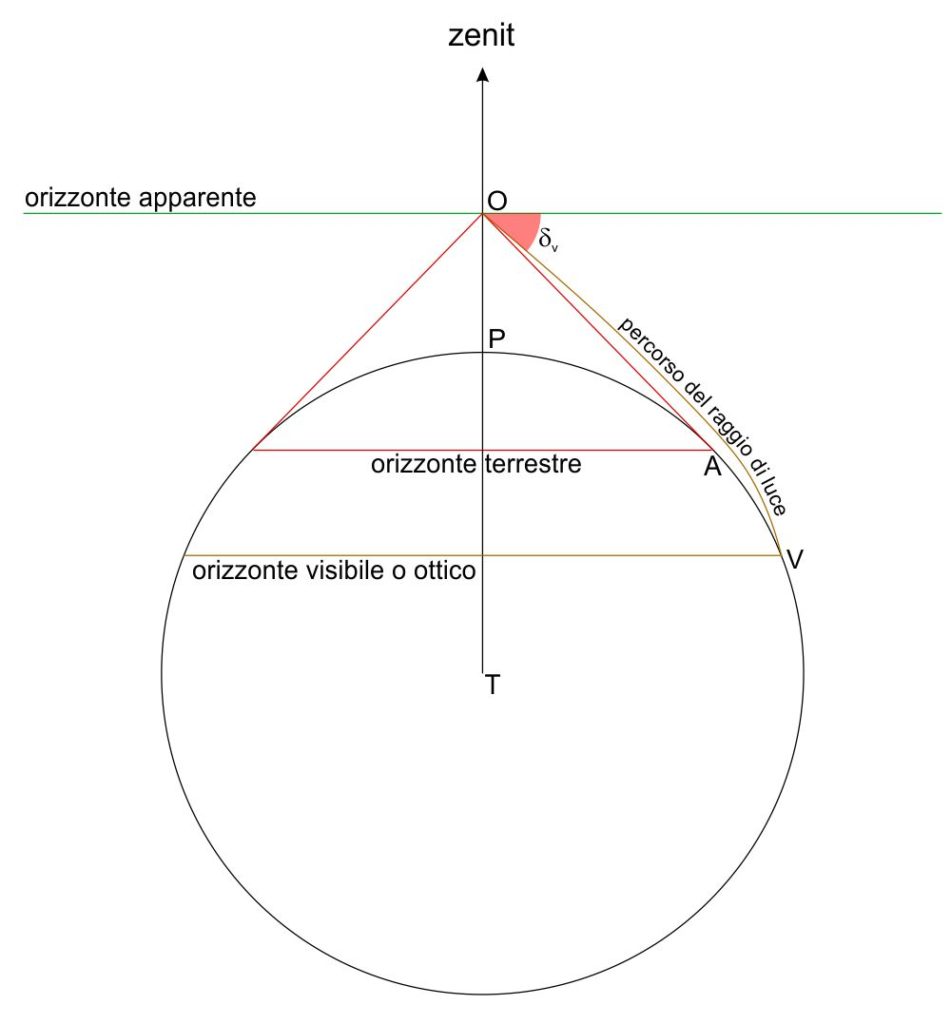
Attraversando strati d’aria a diversa densità, i raggi di luce provenienti dai limiti dell’orizzonte terrestre subiscono una curvatura dovuta alla rifrazione.
Come conseguenza l’osservatore può vedere un po’ oltre l’orizzonte terrestre definito in termini solo geometrici. Il suo sguardo raggiunge quello che viene chiamato orizzonte visibile o ottico. La rifrazione perciò aumenta anche la parte di stelle visibili con un effetto che “solleva” e “comprime” la fascia di cielo prossima all’orizzonte. Tenendo conto della rifrazione, l’angolo di depressione dell’orizzonte $\delta_v$ è leggermente minore di quello che può essere calcolato geometricamente in base alla quota.
Per completezza, definiamo come orizzonte fisico la linea di confine della regione visibile da un dato luogo, tenendo conto anche degli ostacoli naturali, (rilievi, vegetazione, edifici, ecc).
(1)
Se si approssima la forma della Terra ad una sfera e se non si considera la rifrazione atmosferica, il raggio d’orizzonte $r$ si calcola:
$$\boxed{r=\sqrt{h(2R+h)}}$$
dove $R$ è il raggio terrestre e $h$ la quota dell’osservatore sul livello del mare.
La depressione dell’orizzonte $\delta$ in funzione della quota si calcola in questo modo:
$$\boxed{\tan{\delta}=\sqrt{\frac{2h}{R}+\frac{h^2}{R^2}}}$$
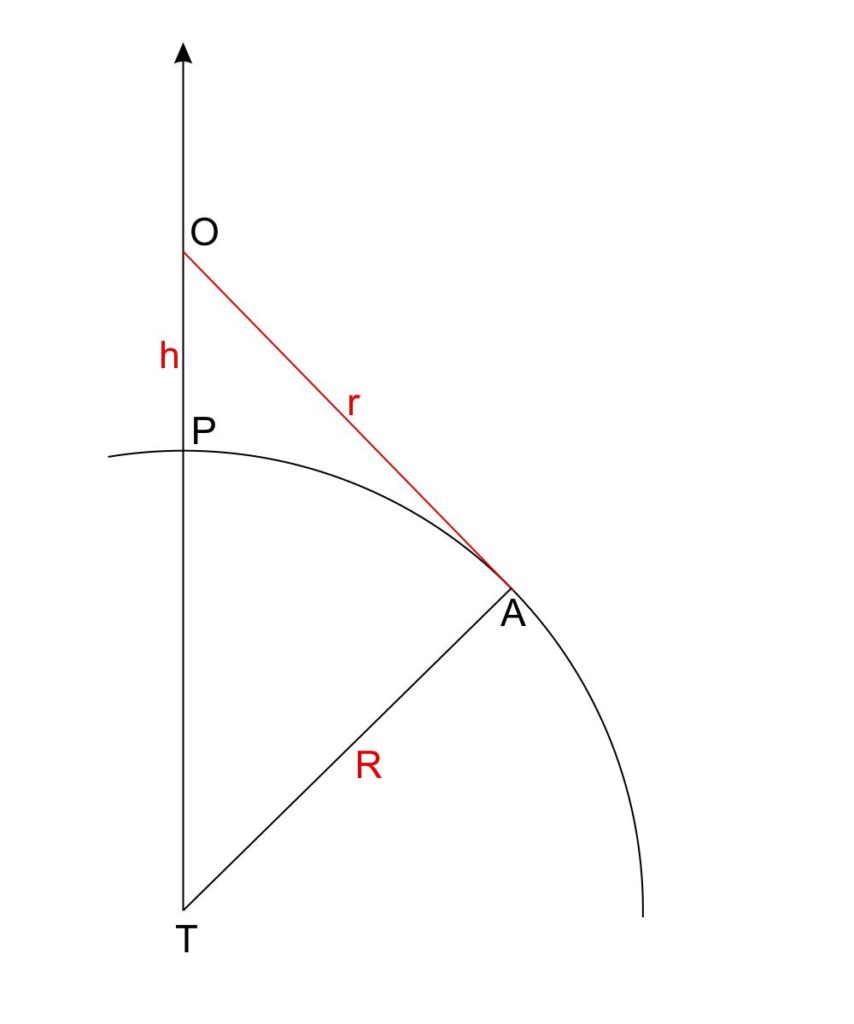
Infatti, essendo il raggio d’orizzonte $r$ tangente alla circonferenza nel punto $A$, il triangolo $TAO$ è retto in $A$. I suoi cateti sono il raggio d’orizzonte $r$ e il raggio terrestre $R$. L’ipotenusa $TO$ è uguale alla somma del raggio terrestre $TP$ e della quota $h$.
Perciò possiamo calcolare $r$ con il teorema di Pitagora:
$r= \sqrt{TO^2-R^2}=$
$\,=\sqrt{(R+h)^2+R^2}=$
$\,=\sqrt{R^2+2Rh+h^2-R^2}=$
$\,=\sqrt{2Rh+h^2}=$
$\,=\sqrt{h(2R+h)}$
L’angolo $\delta$ di depressione dell’orizzonte è uguale all’angolo in $T$ del triangolo $TAO$ e quindi può essere calcolato per via trigonometrica:
$\tan{\delta}=\frac{r}{R}=$
$\,=\frac{\sqrt{h(2R+h)}}{R}$
che si può anche scrivere nella forma:
$\tan{\delta}=\sqrt{\frac{2h}{R}+\frac{h^2}{R^2}}$