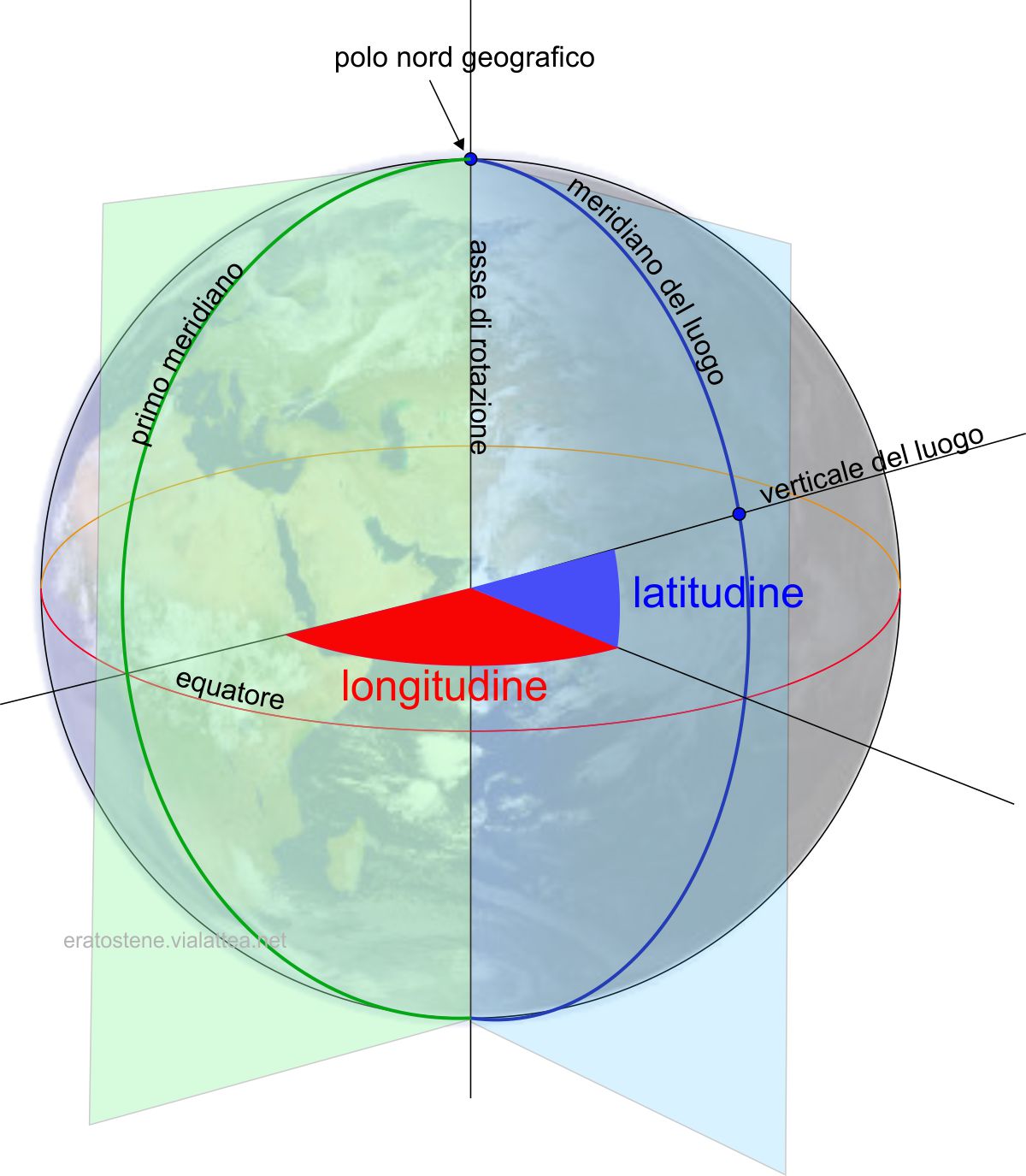
In termini generali, la latitudine e la longitudine geografiche, che identificano la posizione di un punto sulla superficie terrestre rispetto all’equatore e al primo meridiano, sono definite entrambe in base alla verticale che passa per quel punto: infatti, la latitudine è l’angolo formato dalla verticale con il piano equatoriale e la longitudine è l’angolo compreso tra il piano verticale del meridiano del luogo e il piano del meridiano di riferimento.
Se la Terra fosse sferica e di composizione omogenea, la verticale materializzata dal filo a piombo passerebbe per il suo centro e la definizione di una rete dei meridiani e paralleli risulterebbe da semplici leggi di geometria sferica.
Ma la Terra non è sferica, non ha una composizione chimica omogenea e la sua superficie fisica, complicata da rilievi montuosi ed avvallamenti, ha una forma complessiva che si avvicina solo con grande approssimazione a quella di un ellissoide oblato.
Di conseguenza sorge il problema della verticale: quale verticale utilizzare per la misura di latitudine e longitudine? La verticale del filo a piombo, la retta perpendicolare ad un punto della superficie dell’ellissoide oppure la retta che passa per il centro della terra?
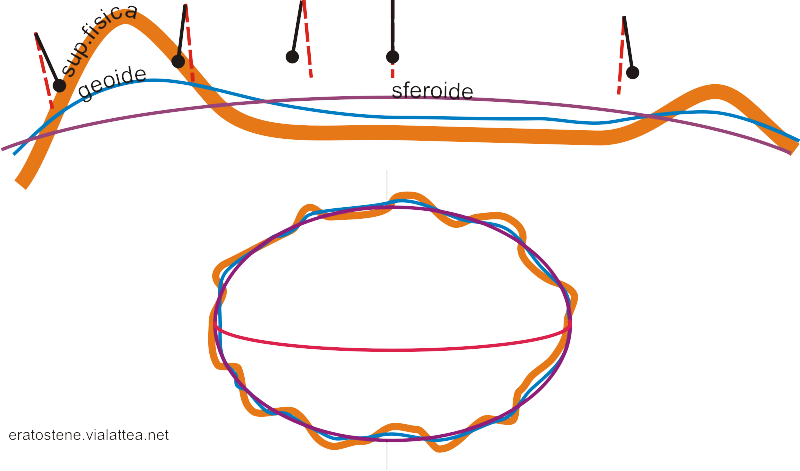
Una prima semplificazione della superficie fisica è il geoide: una superficie ideale, perpendicolare in ogni suo punto al filo a piombo e avente una quota pari al livello medio dei mari. Purtroppo il geoide non può essere facilmente ridotto ad una forma geometrica semplice: l’irregolare distribuzione delle masse di roccia, con massicci montuosi e depressioni e la presenza di masse rocciose a varie densità ne deforma la superficie. Possiamo pensarlo come una superficie ondulata pieno di rigonfiamenti e depressioni irregolari.
Pur “smussando gli spigoli” della forma fisica, il geoide sfugge ancora alla definizione matematica. D’altra parte esso si avvicina ad una forma geometrica precisa: l’ellissoide, cioè una sfera deformata per schiacciamento polare e teorizzata per la prima volta da Newton in base agli effetti fisici del moto di rotazione sulla massa del pianeta. L’ellissoide è definibile matematicamente in base alle misure del raggio polare e del raggio equatoriale. La rete di meridiani e paralleli disegnata sulle carte geografiche si basa sulle coordinate geodetiche relative all’ellissoide.
Per riassumere, abbiamo a disposizione tre diversi sistemi di coordinate geografiche, basati ciascuno, su un diverso tipo di verticale.
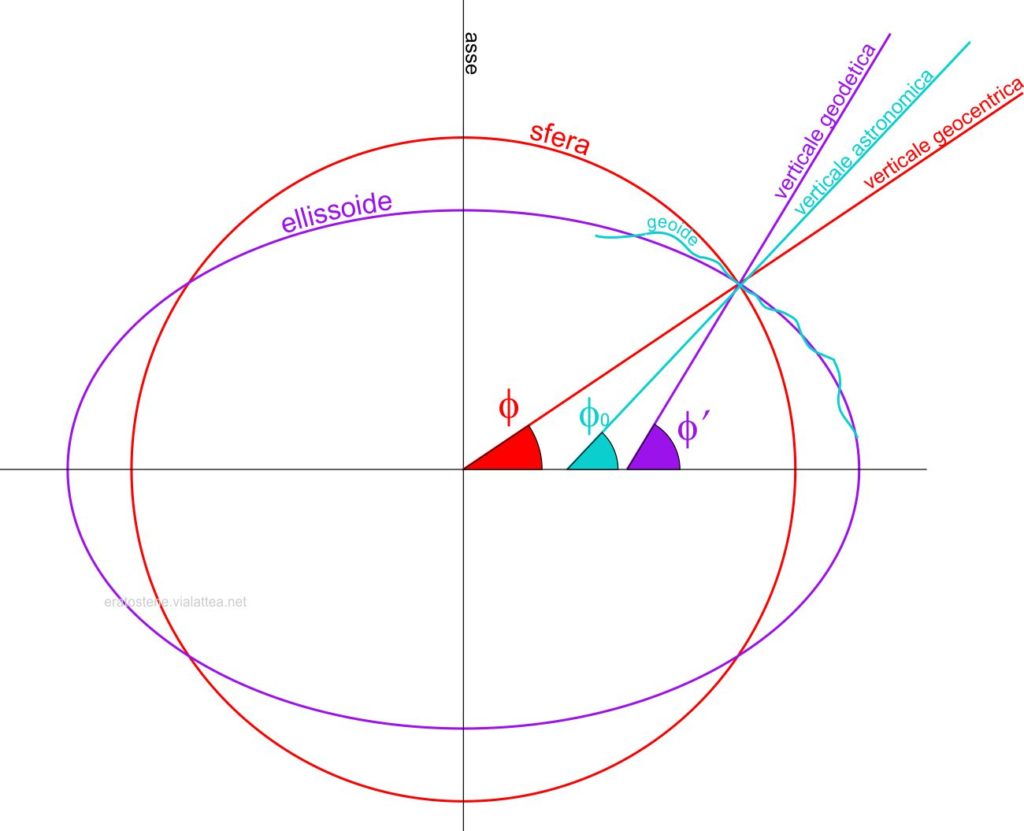
Ogni tipo di verticale produce una sua misura di latitudine: $\phi$: latitudine geocentrica, $\phi_0$: latitudine astronomica e $\phi’$: latitudine geodetica. (nel disegno si esagera volutamente l’eccentricità dello sferoide)
Le coordinate astronomiche (latitudine e la longitudine astronomiche) si basano sulla verticale astronomica, cioè sulla direzione del filo a piombo che è sempre perpendicolare alla superficie del geoide. Sono le coordinate “empiriche”, ottenute dall’osservazione degli astri e dalla misurazione della loro posizione rispetto alla verticale del luogo. La verticale astronomica non passa per il centro della Terra.
Le coordinate geodetiche hanno come riferimento la verticale geodetica, che si definisce come la perpendicolare alla superficie di un ellissoide di riferimento. L’ellissoide di riferimento è una superficie matematica, ideale, scelta in base alla migliore approssimazione alla forma del geoide. La verticale geodetica differisce dalla verticale astronomica in media di 1 secondo d’arco ma può arrivare ad alcune decine di secondi d’arco nei pressi delle montagne. Nemmeno questa verticale passa per il centro della Terra ad eccezione di alcuni punti: ai polo e all’equatore.
Un terzo sistema, detto sistema di coordinate geocentriche, prende come riferimento la verticale geocentrica, cioè una retta che passa per un centro ideale della Terra. La latitudine basata sulla verticale geocentrica e quella geodetica sono legate da una precisa relazione matematica e coincidono solo ai poli e all’equatore. La loro differenza è massima a $45°$ dove raggiunge $\text{11,5}$ secondi d’arco. Le longitudini geodetiche e geocentriche invece coincido in ogni luogo.
La longitudine astronomica differisce dalle due longitudini “matematiche”.
Infatti la longitudine astronomica è l’angolo compreso tra il piano meridiano fondamentale e il piano meridiano celeste dell’osservatore e un piano meridiano è definito come il piano che passa per la verticale astronomica e per i poli celesti. Lo stesso primo meridiano, attuale riferimento per la longitudine geodetica, non coincide esattamente con il meridiano di Greenwich stabilito nella Conferenza di Washington del 1884, essendo quest’ultimo definito in base alla verticale astronomica passante per l'”Airy transit circle” dell’osservatorio e che si pensava intersecasse l’asse di rotazione. I due meridiani sono separati tra loro da una differenza di $\text{0,19}$ secondi d’arco di longitudine.
Gli astronomi utilizzano la latitudine e la longitudine astronomiche per posizionare e direzionare con precisione i loro strumenti; inoltre fanno uso delle coordinate geocentriche per poter condividere con altri osservatori le posizioni degli astri. I cartografi e i navigatori invece utilizzano le coordinate geodetiche.

